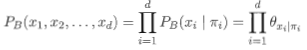先验概率:基于已有知识对司机事件进行概率预估,但不考虑任何相关因素。
后验概率:基于已有知识对随机事件进行概率预估,并考虑相关因素P(c|X)。
7.1 贝叶斯决策论
贝叶斯决策论是概率框架下实施决策的基本方法。贝叶斯决策论考虑如何基于这些概率和误判损失来选择最优的类别标记。
在样本x上的“条件风险”: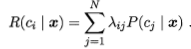
我们的任务是寻找一个判定准则h:以最小化总体风险 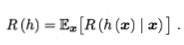
贝叶斯判定准则:为最小化总体风险,只需在每个样本上选择哪个能使条件风险R(c|x)最小的类别标记。
h*称为贝叶斯最优分类器,与之对应的总体风险R(h*)称为贝叶斯风险。1-R(h*)反映了分类器所能达到的最好性能。
最小化分类错误率的贝叶斯最优分类器为 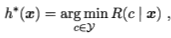 即对每个样本x,选择能使后验概率P(c|x)最大的类别标记。
即对每个样本x,选择能使后验概率P(c|x)最大的类别标记。
机器学习所要实现的是基于有限的训练样本尽可能准确地估计出后验概率P(c|x).大体来说,主要有两种策略:给定x,可通过直接建模P(c|x)来预测c,这样的得到的是“判别式模型”;也可以先对联合概率分布P(x,c)建模,然后再由此获得P(c|x),这样的得到的是“生成式模型”。决策树、BP神经网络、支持向量机等为判别式模型。
对生成式模型有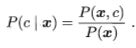 ,基于贝叶斯定理,P(c|x)可写为
,基于贝叶斯定理,P(c|x)可写为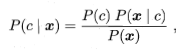 ;
;
类先验概率P(c)表达了样本空间中各类样本所占的比例,根据大数定律,当训练机包含足够多的独立同分布样本是,P(c)可通过各类样本出现的频率来进行估计。
7.2 极大似然估计
估计类条件概率:先假定其具有某种确定的概率分布形式,再基于训练样本对概率分布的参数进行估计。概率模型的训练过程就是参数估计过程。
统计学里的两个学派:频率学派和贝叶斯学派
频率学派:强调概率的“客观性”,概率为客观随机性。模型参数固定,样本随机。认为观察者获得的信息是一样的。认为应该将事件在重复试验中发生的频率作为其发生的概率的估计。认为参数虽然未知,但却是客观存在的确定值,可通过优化似然函数等准则来确定参数值;
贝叶斯学派:强调概率的主观性,即条件概率。样本固定,模型参数视为关键。认为不同的观察者获得的信息是不一样的。认为事情发生概率的客观性仅仅是因为观察者不知道事件的结果。随机性的根源不在于事件,而在于观察者对事件的知识状态。而频率学派则认为随机性的根源就是事件,跟观察者无关。认为参数是未观察到的随机变量,其本身也可以有分布,因此可假定参数服从一个先验分布,然后基于观测到的数据来计算参数的后验分布。
极大似然估计---------频率主义学派
Dc----训练集D中第c类样本组成的集合,假设这些样本独立同分布,则参数θc对数据集Dc的似然是: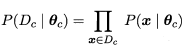 ,对数似然:
,对数似然: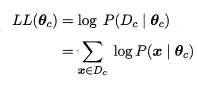
例如在连续情形下,假设概率密度函数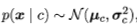 则参数的极大似然估计为:
则参数的极大似然估计为:
也就是说,通过极大似然得到的正态分布均值就是样本均值,方差就是 的均值。
的均值。
7.3 朴素贝叶斯分类器
朴素:属性条件独立
类条件概率P(c|x)是所有属性上的联合概率,难以从有限的训练样本中直接估计而得。
朴素贝叶斯分类器采用了“属性条件独立性假设”:对已知类别,假设所有属性相互独立,换言之,假设每个属性独立地对分类结果产生影响。
基于属性条件独立性假设,有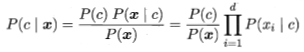 ,对所有类别来说P(x)相同,因此朴素贝叶斯分类器的表达式为:
,对所有类别来说P(x)相同,因此朴素贝叶斯分类器的表达式为: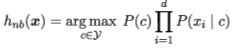
朴素贝叶斯分类器的训练过程就是基于训练集D来估计①类先验概率,并为每个属性估计②条件概率P(xi|c);
类先验概率: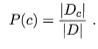 ,条件概率:
,条件概率: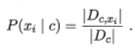
为了避免其他属性携带的信息被训练集中未出现的属性值“抹去”,在估计概率值是通常要进行“平滑”,常用“拉普拉斯修正”。令N表示训练集D中可能的类别数,Ni表示第i个属性可能的取值数,则修正为: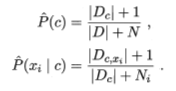
拉普拉斯修正避免了因训练集样本不充分而导致概率估值为零的问题,并且在训练集变大时,修正过程所引入的先验的影响也会准便变得可以忽略。
7.4 半朴素贝叶斯分类器
半朴素贝叶斯分类器的基本想法是适当考虑一部分属性见的相互依赖信息,从而既不需进行完全联合概率计算,又不至于彻底忽略了比较强的属性依赖关系。“独依赖估计”是般朴素贝叶斯的常用策略。“独依赖”就是假设每个属性在类别之外最多仅依赖于一个其他属性,即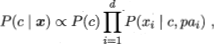 其中pai为属性xi所依赖的属性,称为父属性。
其中pai为属性xi所依赖的属性,称为父属性。
如何确定每个属性的父属性:SPODE方法:假设所有属性都依赖于同一个属性,称为“超父”,然后通过交叉验证等模型选择方法来确定超父属性。
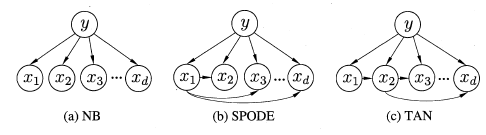
TAN则是在最大带权生成树算法的基础上,通过以下步骤将属性见的依赖关系简约得到如图所示的树形结构:
(1)计算任意两个属性之间的条件互信息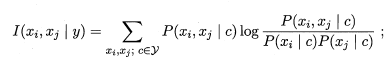
(2)以属性为结点构建完全图,任意两个节点之间边的权重设为
(3)构建此完全图的最大带权生成树,挑选根变量,将边置为有向;
(4)加入类别结点y,增加从y到每个属性的有向边。
TAN实际上仅保留了强相关属性之间的依赖性。
AODE是一种基于集成学习机制、更为强大的独依赖分类器,与SPOED通过模型选择确定超父属性不同,AODE尝试将每个属性作为超父来构建SPODE,然后将那些具有足够训练数据支撑的SPOED集成起来作为最终结果。
7.5 贝叶斯网
贝叶斯网亦称“信念网”,它借助有向无环图来刻画属性之间的依赖关系,并使用条件概率表来描述属性的联合概率分布。
一个贝叶斯网B由结构G和参数Θ两部分构成,即B= <G,Θ>,网络结构G是一个有向无环图,其每个结点对应于一个属性,若两个属性有直接依赖关系,则他们由一条边连接起来;参数Θ定量描述这种依赖关系,假设属性xi在G中父节点即为πi,则Θ包含了每个属性的条件概率表
7.5.1 结构
贝叶斯网结构有效地表达了属性间的条件独立性。给定父节点集,贝叶斯网假设每个属性与他的非后裔属性独立,于是B=<G,Θ>将属性x1,x2,...,xd的联合概率分布定义为: