题目描述
给定一个数组A[0,1,...,n-1],请构建一个数组B[0,1,...,n-1],其中B中的元素B[i]=A[0]*A[1]*...*A[i-1]*A[i+1]*...*A[n-1]。不能使用除法。(注意:规定B[0] = A[1] * A[2] * ... * A[n-1],B[n-1] = A[0] * A[1] * ... * A[n-2];)
对于A长度为1的情况,B无意义,故而无法构建,因此该情况不会存在。
我的思路:
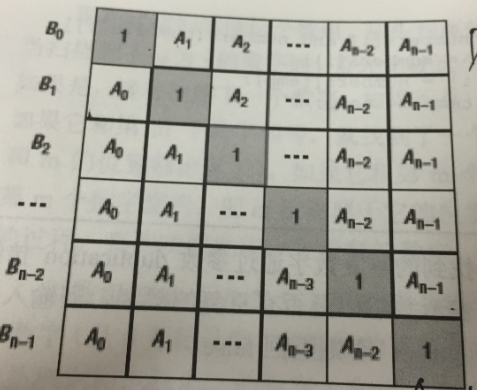
下三角,用连乘,下三角用for循环
但是这样时间复杂度仍然是O(n^2)
class Solution { public: vector<int> multiply(const vector<int>& A) { vector<int> B; int len = A.size(); int frontMul = 1; int backMul = 1; for(int i=0;i<len;i++){ if(i>0) frontMul *= A[i-1]; backMul = 1; for(int j = i+1;j<len;j++){ backMul *= A[j]; } B.push_back(frontMul*backMul); } return B; } };
时间复杂度为O(n)的思路:
C[i]可以用自上而下的顺序计算出来,C[i]=C[i-1]*A[i-1]
D[i]可以使用自下而上的顺序计算出来,D[i]=D[i+1]*A[i+1]
然后返回的结果B[i]=C[i] * D[i]
import java.util.ArrayList; public class Solution { public int[] multiply(int[] A) { int len = A.length; int[] B = new int[len]; int[] C = new int[len]; int[] D = new int[len]; C[0] = 1; D[len-1]=1; for(int i=1;i<len;i++){ C[i] = C[i-1] * A[i-1]; } for(int i=len-2;i>=0;i--){ D[i] = D[i+1] * A[i+1]; } for(int i=0;i<len;i++){ B[i] = C[i] * D[i]; } return B; } }
空间复杂度优化:
class Solution { public: vector<int> multiply(const vector<int>& A) { int len = A.size(); vector<int> B(len,1); for(int i=1;i<len;i++) B[i] = B[i-1]*A[i-1]; int temp = 1; for(int i=len-2;i>=0;i--){ temp *= A[i+1]; B[i] *= temp; } return B; } };