-
二叉树的前序遍历、中序遍历、后序遍历
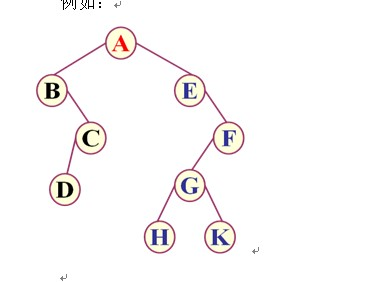
- 前序遍历
- 遍历顺序规则为【根左右】
- ABCDEFGHK
- 中序遍历
- 遍历顺序规则为【左根右】
- BDCAEHGKF
- 后序遍历
- 遍历顺序规则为【左右根】
- DCBHKGFEA
- 前序遍历
-
什么是时间复杂度和空间复杂度
- 时间复杂度
- 是指执行当前算法所消耗的时间
- 空间复杂度
- 是指执行当前算法需要占用多少内存空间
- 评价一个算法的效率主要是看它的时间复杂度和空间复杂度。然后有时候鱼和熊掌不可得兼,所以我们就需要从中去取一个平衡点
- 时间复杂度
-
知道淘汰策略的哪些算法?
-
lru算法如果让你实现你会选择哪种数据结构
- LRU算法的原理(least recently used,最近最少使用):
- LRU的四种实现方式
- LRU-K
- 原理:LRU-K中的K代表最近使用的次数,因此LRU可以认为是LRU-1。LRU-K的主要目的是为了解决LRU算法“缓存污染”的问题,其核心思想是将“最近使用过1次”的判断标准扩展为最近使用过K次
- 实现:相比于LRU,LRU-K需要多维护一个队列,用于记录所有缓存数据被访问的历史。只有当数据的访问次数达到K次的时候,才会将数据放入到缓存中。当需要淘汰数据的时候,LRU-K后淘汰第K次访问时间据当前时间最大的数据。
- 过程
- 数据第一次被访问,加入到访问历史列表
- 如果数据在访问历史列表里后没有达到K次访问,就按照一定的规则(FIFO,LRU)淘汰
- 当访问历史队列中的数据访问次数达到K次以后,将数据索引从历史队列中删除,将数据移到缓存队列中,并缓存此数据,缓存队列重新按照时间排序
- 缓存数据队列中被再次访问之后,重新排序
- 需要淘汰数据的时候,淘汰缓存队列中排在末尾的数据,也就是淘汰倒数第K次访问离现在最久的数据
- 过程
- LRU-K降低了缓存污染带来的问题,命中率比LRU要高,他是一个优先级队列,算法复杂度和代价都相对比较高
- 代价:
- 由于LRU-K还需要记录哪些被访问过、但是还没有放入缓存的对象,所以因此内存消耗会比LRU多;数据量很大的时候,内存消耗会很大
- 他需要基于时间进行排序(可以需要淘汰时在进行排序,也可以即时排序),CPU的消耗会比LRU高
- Two queues(2Q)
- 原理:算法类似LRU-2,不同点在于2Q将LRU-2算法中的访问历史队列(注意这不是缓存数据的)改为一个FIFO缓存队列 就是2Q算法有两个缓存队列,一个FIFO队列另一个是LRU队列
- 实现:当数据第一次敢问的时候,2Q算法将数据缓存在FIFO队列中,当数据第二次被访问的时候,就将数据从FIFO队列中移到LRU队列里面,两个队列各自按照自己的方法淘汰数据
- 实现过程
- 新访问的数据插入到FIFO队列
- 如果数据在FIFO中一直没有被再次访问的话,则最终按照FIFO的规则进行淘汰
- 如果数据在FIFO队列中被再次访问的话,就将数据移动到LRU队列的头部
- 乳沟数据在LRU队列再次被访问,就将数据移到LRU队列的头部
- LRU队列淘汰末尾的数据
- 实现过程
- Multi Queue(MQ)
- 原理:MQ算法根据访问的频率将数据划分成多个队列,不同的队列具有不同的访问的优先级,核心思想就是:优先缓存访问次数多的数据
- 实现:MQ算法将缓存划分为多个LRU队列,每个队列对应不同的访问优先级。访问优先级是根据访问次数计算出来的
- LRU
- 原理:算法根据数据的历史访问记录来进行淘汰数据,其核心思想是”如果数据最近被访问过,那么将来被访问的几率也就更高“
- 实现:最常见是实现是使用一个链表保存缓存数据
- 过程
- 新书插入到链表的头部
- 每当缓存命中(也就是缓存数据被访问的时候),就将移动到链表的头部
- 当链表满的时候,将链表尾部的数据丢弃
- 过程
- LRU-K
- LRU的四种实现方式
- LRU算法的原理(least recently used,最近最少使用):
-
知道动态规划和贪心算法吗
- 动态规划
- 全局最优解中一定包含某个局部最优解,但是不一定包含前一个局部最优解,因此需要记录之前的所有最优解
- 动态规划的关键就是在于状态转移方程,即如何用已经求出的局部最优解来推导全局最优解
- 边界条件:即最简单的,可以直接得出的局部最优解
- 贪心算法
- 问题求解时总是做出当前看是最好的选择,也就是说,不从整体最优上加以考虑,他所作出的仅是在某种意义上的局部最优解
- 作出的每一步贪心决策都是无法改变的,因为贪心决策是由上一步的最优解推导下一步的最优解,而上一步之前的最优解则不做保留
- 贪心算法的正确条件:每一步的最优解一定包含上一步的最优解
- 共同点:都是一种递推算法,均是局部最优解来推导全局最优解
- 动态规划