1.判断一个区域是不是合法的多边形
通过向量来判断,两条线段是否相交,是否规范相交(非端点相交)
向量 在
的 顺时针方向,那么
向量 在
的 逆时针方向,那么
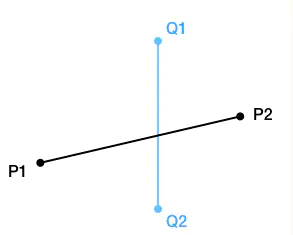
相对于P1P2而言,P1Q1在逆时针方向,P1Q2在顺时针方向,即存在P1Q1 和 P1P2的叉积 与P1Q2 和 P1P2的叉积 的乘积 的 小于零
如果一条的线段的两个端点在另外一条线段两侧,那么这两条线段可能相交
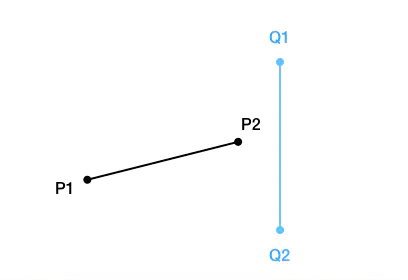
这种情况为没有相交,且乘积也小于0,这种情况就需要换位思考,我们可以把参考物转换为Q1Q2,那么对于Q1Q2而言,Q1P1和Q2P2存在其顺时针。
因此存在四种情况判断两条线段是否规范相交
当 &&
的时候,两条线段规范相交。
换成代码则为:
/* 地图区域线段是否存在非端点的香蕉 setSegment : 确定线段的两个端点 isIntersect: 确定两条线段是否相交 pointIsCrossing: 多边形是否存在相交 */ function setSegment(point1, point2) { return { point1: point1, point2: point2 }; } function isIntersect(line1, line2) { let p1 = line1.point1; let p2 = line1.point2; let q1 = line2.point1; let q2 = line2.point2; let a1 = (p2.lat - p1.lat) * (q1.lng - p1.lng) - (q1.lat - p1.lat) * (p2.lng - p1.lng); let a2 = (p2.lat - p1.lat) * (q2.lng - p1.lng) - (q2.lat - p1.lat) * (p2.lng - p1.lng); let b1 = (q2.lat - q1.lat) * (p1.lng - q1.lng) - (p1.lat - q1.lat) * (q2.lng - q1.lng); let b2 = (q2.lat - q1.lat) * (p2.lng - q1.lng) - (p2.lat - q1.lat) * (q2.lng - q1.lng); if (a1 * a2 < 0 && b1 * b2 < 0) { return true; } return false; } export function pointIsCrossing(points) { let i = 0; let setgments = []; let len = points.length; while (i < len - 1) { setgments.push(setSegment(points[i], points[i + 1])); i++; } setgments.push(setSegment(points[i], points[0])); console.log(setgments, 'setgments'); for (let m = 0; m < setgments.length - 1; m++) { let mS = setgments[m]; for (let n = m + 1; n < setgments.length; n++) { let nS = setgments[n]; if (isIntersect(mS, nS)) { return true; } } } return false; }
2.判断一个点是否在一个区域内
判断规则:以这个点为任意方向做射线,射线与区域的的交点的个数为偶数就在区域外,即无焦点,反之为奇数就在区域内
转为js代码:
export const isPointInPolygon = (point, polygon) => { let N = polygon.length let boundOrVertex = true //如果点位于多边形的顶点或边上,也算做点在多边形内,直接返回true let intersectCount = 0 //cross points count of x let precision = 2e-10 //浮点类型计算时候与0比较时候的容差 let p1, p2 //neighbour bound vertices let p = point //测试点 p1 = polygon[0] //left vertex for (let i = 1; i <= N; ++i) { //check all rays if (p.latitude === p1.latitude && p.longitude === p1.longitude) { return boundOrVertex //p is an vertex } p2 = polygon[i % N] //right vertex if (p.longitude < Math.min(p1.longitude, p2.longitude) || p.longitude > Math.max(p1.longitude, p2.longitude)) { //ray is outside of our interests p1 = p2 continue //next ray left point } if (p.longitude > Math.min(p1.longitude, p2.longitude) && p.longitude < Math.max(p1.longitude, p2.longitude)) { //ray is crossing over by the algorithm (common part of) if (p.latitude <= Math.max(p1.latitude, p2.latitude)) { //x is before of ray if (p1.longitude === p2.longitude && p.latitude >= Math.min(p1.latitude, p2.latitude)) { //overlies on a horizontal ray return boundOrVertex } if (p1.latitude === p2.latitude) { //ray is vertical if (p1.latitude === p.latitude) { //overlies on a vertical ray return boundOrVertex } else { //before ray ++intersectCount } } else { //cross point on the left side let xinters = ((p.longitude - p1.longitude) * (p2.latitude - p1.latitude)) / (p2.longitude - p1.longitude) + p1.latitude //cross point of x if (Math.abs(p.latitude - xinters) < precision) { //overlies on a ray return boundOrVertex } if (p.latitude < xinters) { //before ray ++intersectCount } } } } else { //special case when ray is crossing through the vertex if (p.longitude === p2.longitude && p.latitude <= p2.latitude) { //p crossing over p2 let p3 = polygon[(i + 1) % N] //next vertex if (p.longitude >= Math.min(p1.longitude, p3.longitude) && p.longitude <= Math.max(p1.longitude, p3.longitude)) { //p.longitude lies between p1.longitude & p3.longitude ++intersectCount } else { intersectCount += 2 } } } p1 = p2 //next ray left point } if (intersectCount % 2 === 0) { //偶数在多边形外 return false } else { //奇数在多边形内 return true } }