Vitaly works at the warehouse. The warehouse can be represented as a grid of n × mcells, each of which either is free or is occupied by a container. From every free cell it's possible to reach every other free cell by moving only through the cells sharing a side. Besides that, there are two robots in the warehouse. The robots are located in different free cells.
Vitaly wants to swap the robots. Robots can move only through free cells sharing a side, moreover, they can't be in the same cell at the same time or move through each other. Find out if the swap can be done.
Input
The first line contains two positive integers n and m (2 ≤ n·m ≤ 200000) — the sizes of the warehouse.
Each of the next n lines contains m characters. The j-th character of the i-th line is «.» if the corresponding cell is free, «#» if there is a container on it, «1» if it's occupied by the first robot, and «2» if it's occupied by the second robot. The characters «1» and «2» appear exactly once in these lines.
Output
Output «YES» (without quotes) if the robots can be swapped, and «NO» (without quotes) if that can't be done.
Examples
5 3
###
#1#
#.#
#2#
###
NO
3 5
#...#
#1.2#
#####
YES
题意:给出了一个n*m (n*m<=200000)的字符矩阵,表示地图。矩阵中#表示被占用的地方,‘ . ’表示可以通过的地方,然后在矩阵中有两个数字1,2,分别表示两个机器人。机器人只能往上下左右走,且只能走向元素为‘ . ’的位置,两个机器人不能穿过对方,问你能不能交换两个机器人的位置(并不要求两个机器人同时走)。
思路:这题可以用DFS来写(这道题看了大佬的代码,绕的我头都晕了,对DFS的原理产生了怀疑!看了一天才看懂)
首先我们来分析一下什么情况下可以实现交换,首先两个机器人之间要有通路,但有通路还不够,要有两种情况才行。
第一种:1和2两个机器人之间有回路,就是他们两个在一个环上,那就可以在环上绕一圈,就完成了互换(如样例2)。
第二种:1和2之间有通路,且在机器人能够到达的所有点中,至少有一点的度大于2(度大于2就是说这个点的四个方向,至少三个不是障碍物),看下面的图来理解;
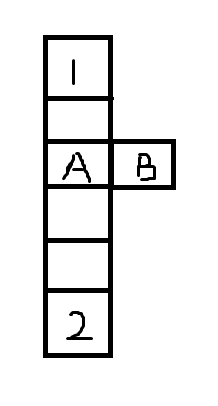
在上面的图中,A点的度就是3,因为他的上下和右都可以走;
如果要完成交换,1号可以先走到 B位置,然后让2号通过,1号再出来,去到2号原本的位置,便完成了交换。
但如果没有像A一样度为3的点,即使1和2有一条通路,也无法交换,因为1和2不能穿过对方。
如果1和2之间有多条通路且1,2不在回路上,那一定有度为3的点或环,因为要从一个点分出两条路来,分出的两条路是两个度,再加上走到这点的路,就是三个度。
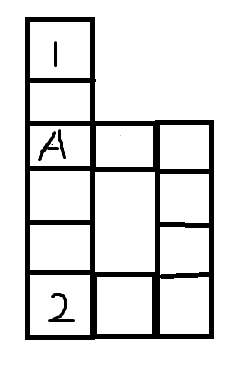
就如上图,1到2有两条路,就一定存在一个如A一样的点,度为3,除非1,2在同一个环上(如样例2);
所以这题就和可以等同于求通路的条数,如果有两条通路(环也可以看成两条路)或一条通路但有一个点的度为3,那就YES,其余全是NO。
具体求法看代码:
1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 #include<string> 5 //#include<cmath> 6 #include<climits> 7 #include<algorithm> 8 #include<stack> 9 #include<queue> 10 #define eps 1e-7 11 #define ll long long 12 #define inf 0x3f3f3f3f 13 #define pi 3.141592653589793238462643383279 14 using namespace std; 15 int dir[4][2] = {1,0,-1,0,0,1,0,-1}; 16 int dot[200005],vis[200005]; 17 int x1,x2,y1,y2,ok,ans,flag; //x1,y1好像会和 cmath头文件里面的东西冲突,所以上面把这个头文件注释掉了 18 int n,m; 19 20 int judge(int x,int y) //计算当前点的度数 21 { 22 int root = 0; 23 if(x-1>=1 && dot[(x-1)*m-m+y] ) 24 root++; 25 if(x+1<=n && dot[(x+1)*m-m+y] ) 26 root++; 27 if(y+1<=m && dot[x*m-m+y+1] ) 28 root++; 29 if(y-1>=1 && dot[x*m-m+y-1] ) 30 root++; 31 return root; 32 } 33 34 void DFS(int x,int y,int cnt) 35 { 36 //cout<<x<<' '<<y<<endl; 37 if( x == x2 && y == y2 ) ans++; //如果走到了终点,ans++; 38 //不用return,因为 可能在终点之后会有度大于2的点 39 if(!flag && x == x1 && y == y1 && cnt > 2 ) 40 //环找到一个就够了,防止出现1和2没有通路,但可以多次回到起点的情况,所以限制只走到起点一次 41 { 42 ans++; 43 flag = 1; 44 } 45 46 if( (!(ans==1 && flag) && (ans && ok) )|| ans>2 || vis[x*m-m+y] ) return; 47 //注意里面的判断条件,回溯的条件在这里面,而ans++的操作在上面,放在这里是为了防止你在将终点标记为走过后,就再也不能走到终点了 48 //ans要大于2而不是等于2,等于2不一定就是有两条路; 49 //因为照我这种写法,走到下一个点之后,从那个点遍历四个方向,还会回到终点,并在回溯前ans++,所以ans会重复计算一次; 50 //如果终点的度是2,并且只有一条路到终点,ans也会等于2,因为重复计算了一次,所以ans要大于2; 51 //终点的度为三时重复计算了两次,但不用在意,因为当有一个点的度为大于2时,有一条通路就够了,并不影响结果; 52 53 vis[x*m-m+y] = 1; 54 55 if(!ok) //如果还没找到度大于2的点 56 { 57 if(judge(x,y) > 2) //就判断当前点的度是否为 3 58 ok = 1; 59 } 60 61 for(int i=0; i<4; ++i) 62 { 63 int xx = x + dir[i][0]; 64 int yy = y + dir[i][1]; 65 if(xx>=1 && xx<=n && yy>=1 && yy<=m && dot[xx*m-m+yy]) 66 { 67 DFS(xx,yy,cnt+1); 68 } 69 } 70 return; 71 } 72 73 int main() 74 { 75 char a; 76 cin>>n>>m; 77 ok = ans = flag = 0; 78 memset(vis,0,sizeof(vis)); //vis标记已走过的点,防止重复走 79 memset(dot,0,sizeof(dot)); //dot标记可以为'.'的点 80 for(int i=1; i<=n; ++i) 81 { 82 getchar(); 83 for(int j=1; j<=m; ++j) 84 { 85 scanf("%c",&a); 86 if(a != '#') 87 dot[i*m-m+j] = 1; 88 if(a == '1') //记录机器人1的位置 89 { 90 x1 = i; 91 y1 = j; 92 } 93 if(a == '2') //记录机器人2的位置 94 { 95 x2 = i; 96 y2 = j; 97 } 98 } 99 } 100 101 DFS(x1,y1,0); //深搜 102 103 if(ans == 1 && flag) //如果ans等于1,但flag=1,表示这个ans是走到起点才加上的,1和2之间并没有通路 104 cout<<"NO"<<endl; 105 else if( (ans && ok) || ans>2 ) 106 cout<<"YES"<<endl; 107 else cout<<"NO"<<endl; 108 return 0; 109 } 110 /* 111 5 3 112 ### 113 #1# 114 #.# 115 #2# 116 ### 117 3 5 118 #...# 119 #1.2# 120 ##### 121 */
上面的代码ans为什么要大于2比较难理解,可以试一下这一组样例,将搜索的每一步输出帮助理解:
3 3
1..
.#.
..2
输出的ans是3,且每一步走的是:
1 1
2 1
3 1
2 1
3 2
3 3 //ans++
2 3
3 3 //ans++
1 3
2 3
1 2
1 3
1 1
3 2
3 1
1 1 //ans++
1 2
可以看到,ans加了三次,而其中的第二次是重复计算,重复计算终点的次数等于终点的度-1;
首先只有能走到终点才会重复计算,当终点的度为2时重复计算了一次,所以ans==3才算有两条路,度为1时不会重复计算,度为3或4时无影响,因为有度为3的点时只要有通路就满足交换条件。
当然,还要防止起点被重复计算,所以标记只能走到起点一次。
还有,在代码中,即使这点标记为走过,还是要继续递归,因为不然终点被标记后就永远也走不到终点了。