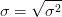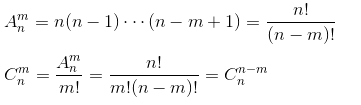【Tips】:转载汇总,参考链接见最后,强烈建议看看原链接,可以收获很多
1.基本概念
- 平均值:所有数据相加 / 数据个数
- 中位数:将数据升序排列,数据项个数为奇数时取中间数,为偶数时取中间两数平均值
- 众数:出现次数最多的数
- 四分位数:数据升序,位于第25%位置的叫做第一四分位数Q1,位于第50%位置的叫做第二四分位数Q2,位于第75%的叫做第三分位数Q3
- 方差:各个数据分别与其平均数之差的平方和的平均数
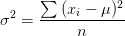
- 方差越小,数据的离散程度越小,数据越稳定
- 标准差:方差开方
- 频数分布:表示互不重叠的组别中每一组项目的个数(若是分类,则是每类数据的总数)
- 偏态:数据的分布情况
- 如果平均数大于众数,称为正偏态/左偏态;相反,则称为负偏态/右偏态
- 概率:描述事件发生的可能性,取值在0-1之间
- 排列组合
- 事件:样本空间的一个子集
- 互斥事件:在试验中两个事件A、B不可能同时发生,可能有多于两种可能
- 独立事件:事件(A或B)是否发生对事件(B或A)发生的概率没有影响
- 对立事件:一件事有两种可能,不是A,就是B
- 条件概率:某个事件A发生的可能性受到另外一个事件B的影响,记作P(A|B)
- 概率公式
- 加法公式:P(A∪B) = P(A)+P(B) - P(A∩B)
- 乘法公式:相互独立的情况下 P(AB)=P(A)P(B)
- 条件概率:
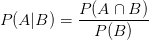
- 贝叶斯公式:
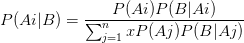
-
随机变量:试验的结果,将每一个可能出现的试验结果赋予了一个数值,包含离散型随机变量和连续型随机变量
- 离散型期望:
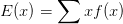
- 离散型方差:
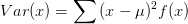
- 二项分布(离散型)
- 当我们要计算抛硬币n次,恰巧有x次正面朝上的概率:

- 期望为E(x) = np,方差Var(x) = np(1-p)
- 当我们要计算抛硬币n次,恰巧有x次正面朝上的概率:
-
泊松分布(离散型)
- 成立条件是在任意两个长度相等的区间中,时间发生的概率是相同的,并且事件是否发生都是相互独立的
- x代表发生x次,u代表发生次数的数学期望,概率函数为:

- 数学期望和方差相等
- 正态分布(连续型)
- u代表均值,σ代表标准差:

- 均值表示正态分布的左右偏移,标准差决定曲线的宽度和平坦,标准差越大曲线越平坦
-
正态随机变量有69.3%的值在均值加减一个标准差的范围内,95.4%的值在两个标准差内,99.7%的值在三个标准差内
- 均值u=0,标准差σ=1的正态分布叫做标准正态分布:
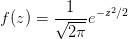
- u代表均值,σ代表标准差:
- 累计分布函数
-
P(X<=x)表示随机变量小于或者等于某个数值的概率,F(x) = P(X<=x)
- 概率密度函数的积分
-
- 抽样:通过样本来推断总体,抽样结果提供的仅仅是相应总体特征的估计
- 点估计:把总体的平均值标准差等称为总体参数,把样本的种种指标称为点估计量
- 是样本标准差,σ是总体标准差。n是样本,N是总体
- 点估计在原有的符号上加横线表示,比如样本均值
,念做x拔
- 样本均值x拔是一个随机变量,称它的概率分布为x拔的抽样分布
- 每次抽样得出的不同均值,必然会有一个期望值,E(x拔) = u,E(x拔)就是所有大量抽样的可能值的均值
- 根据统计学中的中心极限定理,当样本数足够时(n>30),x拔的抽样分布可近似于正态分布
- 无偏估计:当点估计量的期望值等于总体参数时,称为无偏估计
- 样本标准差
- 当样本量占总体5%以上时,有求样本标准差公式:
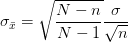
- 当样本量占总体5%以下时,公式可以简化成:

- 当样本量占总体5%以上时,有求样本标准差公式:
- 区间估计
- 通过区间值估计总体情况
- 总体均值的区间估计公式:
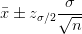
- 置信水平:Zσ/2,之所以除2是因为正态分布左右对称
- 为了获得更高的置信水平,必然会得到更宽的置信区间
- 假设检验
- 对总体参数做一个尝试性的假设
- 该尝试性的假设称为原假设,然后定义一个和原假设完全对立的假设叫做备选假设
- 假设检验就是通过样本数据对两个对立假设进行检验
2.各种定理
(1)切比雪夫定理
- 至少有75%的数据值与平均数的距离在2个标准差以内,至少有89%的数据与平均数在3个标准差之内,至少有94%的数据与平均数在4个标准差以内
- 可以快速掌握数据的范围
- 如果数据本身符合正态(钟形)分布
- 68%的数据落在距离平均数1个标准差内,95%的数据值落在距离平均数2个标准差之内,几乎所有的数据落在3个标准差内
3.图表相关
(1)箱线图
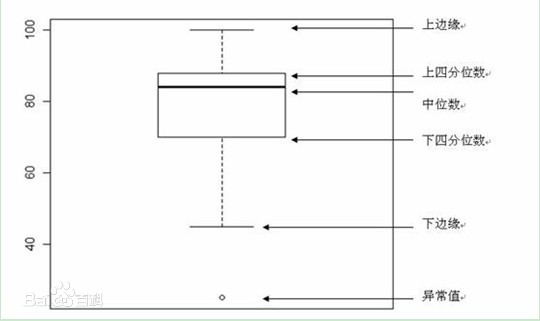
- 需要数据:最小值、第一四分位数Q1、中位数、第三四分位数Q3、最大值
- 下边缘:最小值;上边缘:最大值
- 定义四分位差IQR=Q3(75%分位数)—Q1(25%分位数),箱线图的界限在(Q1-1.5IQR,Q3+1.5个IQR)处
- 界限外部所有值均为异常值
- 箱线图可以读出数据的整体分布和倾斜趋势
(2)直方图


- 标准型:中间高,两边低,呈中间的集中趋势,代表一种稳定正常的形态
- 双峰型:一般是混合了多种数据源或者类别数据造成的
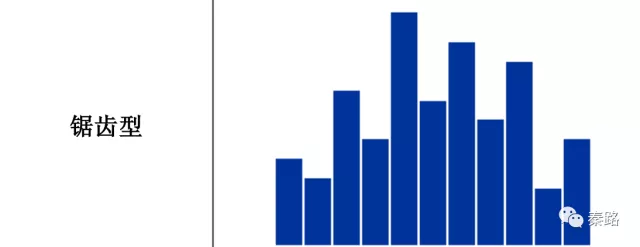

- 锯齿型:一般是观察数据的手段和方法不稳定,才会造成直方图的波动
- 孤岛型:一般是业务上的非正常错误,比如工程零部件出了问题、产品出现了某Bug,造成凸出一块


- 陡壁型:往往是数据源缺失,或者被剔除一部分后,造成这种断崖式的折断
- 偏锋型:分为左偏峰和右偏峰。我们也把它称呼为偏态,上图是一个右偏态
参考链接
- 描述统计:https://mp.weixin.qq.com/s/watt4veiF3NVw2cBpF3f8w
- 描述统计(2):https://mp.weixin.qq.com/s/waoel4g6vwM1Nsao7qvA7g
- 箱线图:https://baike.baidu.com/item/%E7%AE%B1%E5%BD%A2%E5%9B%BE/10671164?fromtitle=%E7%AE%B1%E7%BA%BF%E5%9B%BE&fromid=10101649&fr=aladdin
- 对立、互斥事件:https://www.zhihu.com/question/290506686
- 概率论入门:https://mp.weixin.qq.com/s/jjrOg1CoqlYHrWJe3rRPDQ
- 概率分布:https://mp.weixin.qq.com/s/39Bm5voRoAkaoxnaCzR3Ag
- 假设检验:https://mp.weixin.qq.com/s/21sSP7lzXEEQhjpw3uc3ag