先选先赢问题

一，问题描述

说有偶数个数字，alex和lee两个人比赛，每次轮流从第一个数字或最后一个数字中拿走一个（偶数个数字，所以他俩拿的数字个数相同），最后比谁拿的数字总和大。题目是让我们设计一个算法，对于任意给定的一系列数字，判断如果alex先选，是否一定赢（所有数加起来是奇数，所以不存在平局）？比如有，

[4,3,5,9,11,6,2,1]
alex拿掉开头的4，剩下，

[3,5,9,11,6,2,1]
lee再拿掉开头的3，剩下

[5,9,11,6,2,1]
以此类推。

二，问题分析

首先这里问的是“是否一定赢”，我先举个反例，[4,4,6,8,2,3]，这个先选序列是[4,6,3]，后选是[4，8，2]，后面讨论胜率问题。

三，实验

就随便写一写直接贴代码吧：

import random
import datetime
import matplotlib.pyplot as plt

starttime = datetime.datetime.now()
lenth_list = 10
iterations = 100

A,L = 0,0
x = []
winrate = []
for n in range(1,101):
    x.append(n*iterations)
    for i in range(0,n*iterations):

        list = []
        for i in range(0, lenth_list):
            n = random.randint(0, lenth_list)
            list.append(n)
        # print(list)

        Alex = []
        Lee = []

        while len(list) > 0:
            min_num = 0
            max_num = len(list)-1
            #print(max_num)
            if list[min_num] > list[max_num]:
                #print("Alex")
                Alex.append(list[min_num])
                list.remove(list[min_num])
            else:
                Alex.append(list[max_num])
                list.remove(list[max_num])

            #print("changdu",len(list))

            if list[min_num] > list[max_num-1]:
                Lee.append(list[min_num-1])
                list.remove(list[min_num-1])
                #print("Lee")
            else:
                Lee.append(list[max_num-1])
                list.remove(list[max_num-1])
        if sum(Alex) > sum(Lee):
            A = A + 1
        else:
            L = L + 1
        print(sum(Alex),sum(Lee))
    #print("The win-rate of second man:",L/(A+L)*100,"%")
    winrate.append(L/(A+L)*100)
print(x)
print(winrate)
print(len(winrate))
endtime = datetime.datetime.now()
print (endtime - starttime)

plt.plot(x, winrate, label='First choose first win')
#plt.plot(x2, y2, label='Second Line')
plt.xlabel('Iterations')  #横坐标标题
plt.ylabel('Winrate for second man')  #纵坐标标题
#plt.title('Interesting Graph
Check it out',loc="right")   #图像标题
#plt.title('Interesting Graph
Check it out')
plt.legend()    #显示Fisrt Line和Second Line（label）的设置
plt.savefig('C:/Users/zhengyong/Desktop/1.png')
plt.show()

图示：

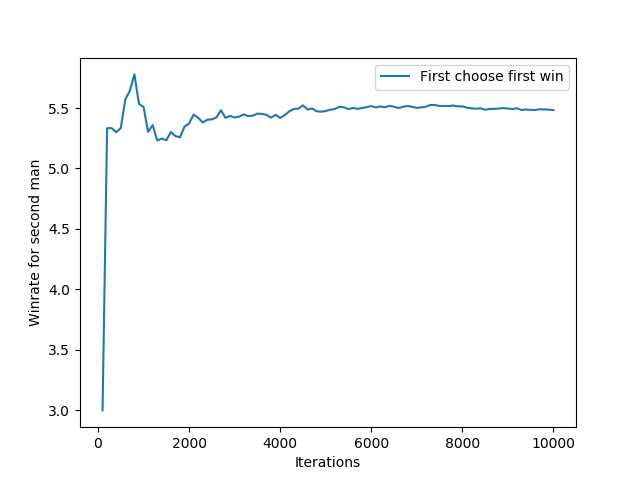
四，结论

这是我在知乎看到的一个问题，这里之所以把这个问题拿出来讲呢，是因为我认为先选不一定先赢（虽然赢面很大），所以特地用生成随机数的方法去验证了一下，发现确实不上先选的一定赢，这里根据长度为10的数组分别迭代100到10000次得到相应的数据，发现，第二个人还是有赢面的，基本稳定在5.5%左右。