协同旋转不变网格形变

　　1.设置网格顶点局部标架

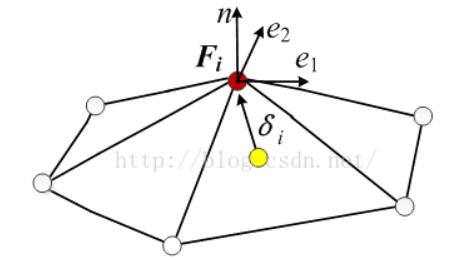
　　定义顶点 Vi 的局部标架 Fi = (ei1, ei2, ni)，如图

　　

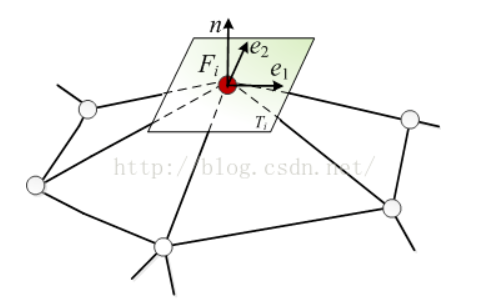
　　三维空间中的任意向量 A 可用局部标架表示为 A = λ1e1 + λ2e2 + λ3n;

　　2.求取矩阵 T

　　两两局部标架之间有旋转矩阵 T（因为是局部标架而非局部坐标系，所以没有平移，不适用合同变换），如下

　　

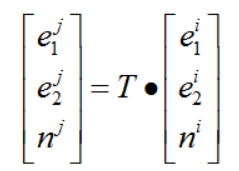
　　每个顶点的标架矩阵 F 都是3 x 3的矩阵，设Fi = (ei1, ei2, ni)和 Fj = (ej1, ej2, nj)为顶点Vi 和 Vj的标架矩阵，Vj 为Vi 的一环邻域顶点，如图

　　

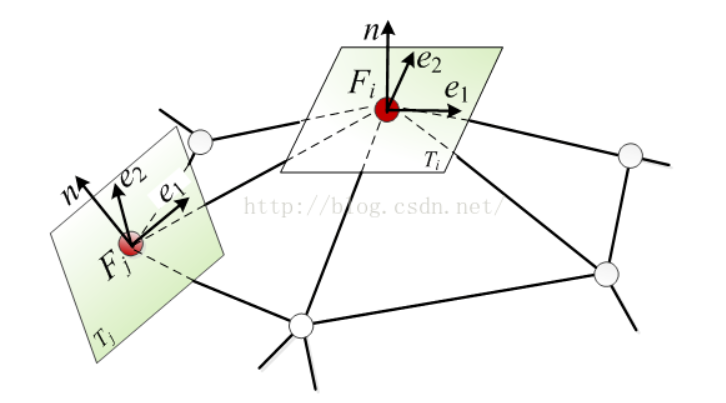
　　则对于旋转矩阵 Tij，有 Fj - TijFi = 0; 调整一下为 Tij 等于 Fj 乘以 Fi的逆。当世界坐标系发生变换时，标架 Fi 和 Fj 同样发生变化，但是矩阵 Tij 是不变的。

　　此为网格的内在属性。

　　3.求取更新后的局部标架

　　和之前那篇，求取拉普拉斯矩阵差不多。只是网格顶点变化为 3 x 3 的矩阵而已，如下

　　

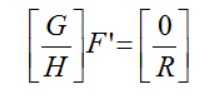
　　关于矩阵 G ，其中每一行的分量是为顶点 Vi 对于其一阶邻域顶点 Vj 的旋转矩阵 Tji ，每一列的分量是为 一阶邻域顶点 Vj 到 顶点 Vi 的旋转矩阵 Tij

　　关于矩阵 H ，和拉普拉斯矩阵中的约束调参顶点一样，但是要修改为 3 x 3的单位矩阵 i。 当 R矩阵中的约束顶点标架发生变化时，便可以求取新的顶点标架 F ' 。

　　4. 求取旋转不变网格之后的拉普拉斯网格形变

　　和之前求取拉普拉斯坐标δ一样，只是需要将全局拉普拉斯坐标转换为局部标架下的局部拉普拉斯坐标δi

　　

　　,

　　当步骤3求取到每个顶点的新标架F之后，求取新的局部拉普拉斯坐标，进而求得拉普拉斯坐标。之后就可以和求取拉普拉斯算子矩阵方程一样，解稀疏线性方程组。

　　

　　

　　

　　

　　构建局部标架以及原始旋转矩阵T和局部拉普拉斯坐标

void mainNode::InitAxesAndMatrixSelf()
{
    //先构建局部坐标系
    for (int i = 0; i < m_vecAllVertex.size(); i++)
    {
        pVERTEX pVertex = m_vecAllVertex.at(i);
        std::vector<pTRIANGLE> vectorTri = pVertex->vecNeighborTri;
        osg::Vec3 vertexNormal, E1, E2;
        vertexNormal = E1 = E2 = osg::Vec3(0.0, 0.0, 0.0);
        int sizeOfTri = vectorTri.size();
        for (int j = 0; j < sizeOfTri; j++)
        {
            pTRIANGLE pTri = vectorTri.at(j);
            pVERTEX pA = pTri->pA;
            pVERTEX pB = pTri->pB;
            pVERTEX pC = pTri->pC;
            osg::Vec3 BA = pA->pos - pB->pos;
            osg::Vec3 BC = pC->pos - pB->pos;
            osg::Vec3 normal = BA ^ BC;
            normal.normalize();
            vertexNormal += normal;
        }
        vertexNormal /= sizeOfTri;
        E1 = osg::Vec3( - vertexNormal.y(), vertexNormal.x(), 0.0);
        E2 = vertexNormal ^ E1;
        vertexNormal.normalize();
        E1.normalize();
        E2.normalize();
        pVertex->E1 = E1;
        pVertex->E2 = E2;
        pVertex->N = vertexNormal;
        pVertex->axesSelf.resize(3, 3);
        std::vector<Eigen::Triplet<float>> vectorTriplet;
        vectorTriplet.push_back(Eigen::Triplet<float>(0, 0, E1.x()));
        vectorTriplet.push_back(Eigen::Triplet<float>(1, 0, E1.y()));
        vectorTriplet.push_back(Eigen::Triplet<float>(2, 0, E1.z()));

        vectorTriplet.push_back(Eigen::Triplet<float>(0, 1, E2.x()));
        vectorTriplet.push_back(Eigen::Triplet<float>(1, 1, E2.y()));
        vectorTriplet.push_back(Eigen::Triplet<float>(2, 1, E2.z()));

        vectorTriplet.push_back(Eigen::Triplet<float>(0, 2, vertexNormal.x()));
        vectorTriplet.push_back(Eigen::Triplet<float>(1, 2, vertexNormal.y()));
        vectorTriplet.push_back(Eigen::Triplet<float>(2, 2, vertexNormal.z()));

        Eigen::SparseMatrix<float> matrixTemp(3, 3);
        matrixTemp.setFromTriplets(vectorTriplet.begin(), vectorTriplet.end());
        pVertex->axesSelf = matrixTemp;
        //构建相对局部坐标系的拉普拉斯坐标长度分量
        pVertex->relativeX = pVertex->lplsPos * E1;
        pVertex->relativeY = pVertex->lplsPos * E2;
        pVertex->relativeZ = pVertex->lplsPos * vertexNormal;
    }
    //构建周围一阶顶点到此顶点的转换矩阵
    for (int i = 0; i < m_vecAllVertex.size(); i++)
    {
        pVERTEX pVertex = m_vecAllVertex.at(i);
        Eigen::Matrix3f axesSelf = pVertex->axesSelf;
        //Eigen::Matrix3f matrixSelf = axesSelf;
        std::vector<pVERTEX> vecNeighborVertex = pVertex->vecNeighborVertex;
        for (int j = 0; j < vecNeighborVertex.size(); j++)
        {
            pVERTEX pNeighbor = vecNeighborVertex.at(j);
            Eigen::Matrix3f axesOther = pNeighbor->axesSelf;
            //std::cout << axesOther << std::endl;
            Eigen::Matrix3f axesOtherInverse = axesOther.inverse();
            //std::cout << axesOtherInverse << std::endl;
            // Ax = b; T * axesOther = axesSelf;
            Eigen::Matrix3f  matrixT = axesSelf * axesOtherInverse;
            pVertex->mapMatrixOtherToSelf.insert(std::pair<int, Eigen::Matrix3f>(pNeighbor->id, matrixT));
            //test
            Eigen::Matrix3f matrixTemp = matrixT * axesOther;
            //std::cout << matrixTemp << std::endl;
            //std::cout << axesSelf << std::endl;
        }
    }
}

　　构建旋转矩阵方程组

void mainNode::InitNewAxesMatrix()
{
    int sizeOfVertex = m_vecAllVertex.size();
    std::vector<Eigen::Triplet<float> > vectorTriplet;
    for (int i = 0; i < sizeOfVertex; i++)
    {
        pVERTEX pVertex = m_vecAllVertex.at(i);
        int vertexID = pVertex->id;
        float sizeOfNeighborVertex = pVertex->vecNeighborVertex.size();
        
        vectorTriplet.push_back(Eigen::Triplet<float>(vertexID * 3, vertexID * 3, - sizeOfNeighborVertex));
        vectorTriplet.push_back(Eigen::Triplet<float>(vertexID * 3 + 1, vertexID * 3 + 1, - sizeOfNeighborVertex));
        vectorTriplet.push_back(Eigen::Triplet<float>(vertexID * 3 + 2, vertexID * 3 + 2, - sizeOfNeighborVertex));

        std::map<int, Eigen::Matrix3f>::iterator itorOfT;
        for(itorOfT = pVertex->mapMatrixOtherToSelf.begin(); itorOfT != pVertex->mapMatrixOtherToSelf.end(); itorOfT++)
        {
            int vertexNeighborID = itorOfT->first;
            Eigen::Matrix3f T = itorOfT->second;
            vectorTriplet.push_back(Eigen::Triplet<float>(vertexID * 3, vertexNeighborID * 3, T(0, 0)));
            vectorTriplet.push_back(Eigen::Triplet<float>(vertexID * 3, vertexNeighborID * 3 + 1, T(0, 1)));
            vectorTriplet.push_back(Eigen::Triplet<float>(vertexID * 3, vertexNeighborID * 3 + 2, T(0, 2)));

            vectorTriplet.push_back(Eigen::Triplet<float>(vertexID * 3 + 1, vertexNeighborID * 3, T(1, 0)));
            vectorTriplet.push_back(Eigen::Triplet<float>(vertexID * 3 + 1, vertexNeighborID * 3 + 1, T(1, 1)));
            vectorTriplet.push_back(Eigen::Triplet<float>(vertexID * 3 + 1, vertexNeighborID * 3 + 2, T(1, 2)));

            vectorTriplet.push_back(Eigen::Triplet<float>(vertexID * 3 + 2, vertexNeighborID * 3, T(2, 0)));
            vectorTriplet.push_back(Eigen::Triplet<float>(vertexID * 3 + 2, vertexNeighborID * 3 + 1, T(2, 1)));
            vectorTriplet.push_back(Eigen::Triplet<float>(vertexID * 3 + 2, vertexNeighborID * 3 + 2, T(2, 2)));
        }
    }
    //添加约束顶点;头一圈和尾一圈,可自己调节
    for (int i = 0; i < m_iAroundNumber * 2; i++)
    {
        pVERTEX pVertex;
        int vertexID;
        float value = 1.0;
        if (i < m_iAroundNumber)
        {
            pVertex = m_vecAllVertex.at(i);
            vertexID = pVertex->id;
        }
        else
        {
            pVertex = m_vecAllVertex.at(i + m_iAroundNumber * (m_iHeightNumber - 2));
            vertexID = pVertex->id;
        }
        vectorTriplet.push_back(Eigen::Triplet<float>(sizeOfVertex * 3 + i * 3, vertexID * 3, value));
        vectorTriplet.push_back(Eigen::Triplet<float>(sizeOfVertex * 3 + i * 3 + 1, vertexID * 3 + 1, value));
        vectorTriplet.push_back(Eigen::Triplet<float>(sizeOfVertex * 3 + i * 3 + 2, vertexID * 3 + 2, value));
    }

    m_NewAxesMatrix.resize(sizeOfVertex * 3 + (m_iAroundNumber * 2 * 3), sizeOfVertex * 3);
    m_NewAxesMatrix.setFromTriplets(vectorTriplet.begin(), vectorTriplet.end());
}

　　求取新的局部标架并获得新的拉普拉斯坐标

void mainNode::CalculateNewAxes()
{
    Eigen::SparseMatrix<float> matrixNewAxesTrans = m_NewAxesMatrix.transpose();
    Eigen::SparseMatrix<float> matrixRes = matrixNewAxesTrans * m_NewAxesMatrix;
    Eigen::SimplicialCholesky<Eigen::SparseMatrix<float> > matrixCholesky(matrixRes);

    std::vector<Eigen::Triplet<float> > vectorTriplet;
    int sizeOfVertex = m_vecAllVertex.size();
    //方程式等号右边
    Eigen::VectorXf vectorX, vectorY, vectorZ;
    vectorX.resize(sizeOfVertex * 3 + m_iAroundNumber * 2 * 3);
    vectorX.setZero();
    vectorY.resize(sizeOfVertex * 3 + m_iAroundNumber * 2 * 3);
    vectorY.setZero();
    vectorZ.resize(sizeOfVertex * 3 + m_iAroundNumber * 2 * 3);
    vectorZ.setZero();
    for (int i = 0; i < m_iAroundNumber * 2; i++)
    {
        pVERTEX pVertex;
        int vertexID;
        Eigen::Matrix3f matrixSelf;
        float value = 1.0;
        if (i < m_iAroundNumber)
        {
            pVertex = m_vecAllVertex.at(i);
        }
        else
        {
            pVertex = m_vecAllVertex.at(i + m_iAroundNumber * (m_iHeightNumber - 2));    
        }
        vertexID = pVertex->id;
        matrixSelf = pVertex->axesSelf;

        vectorX[sizeOfVertex * 3 + i * 3] = matrixSelf(0, 0);
        vectorX[sizeOfVertex * 3 + i * 3 + 1] = matrixSelf(1, 0);
        vectorX[sizeOfVertex * 3 + i * 3 + 2] = matrixSelf(2, 0);

        vectorY[sizeOfVertex * 3 + i * 3] = matrixSelf(0, 1);
        vectorY[sizeOfVertex * 3 + i * 3 + 1] = matrixSelf(1, 1);
        vectorY[sizeOfVertex * 3 + i * 3 + 2] = matrixSelf(2, 1);

        vectorZ[sizeOfVertex * 3 + i * 3] = matrixSelf(0, 2);
        vectorZ[sizeOfVertex * 3 + i * 3 + 1] = matrixSelf(1, 2);
        vectorZ[sizeOfVertex * 3 + i * 3 + 2] = matrixSelf(2, 2);
    }
    
    vectorX = matrixNewAxesTrans * vectorX;
    vectorY = matrixNewAxesTrans * vectorY;
    vectorZ = matrixNewAxesTrans * vectorZ;

    Eigen::VectorXf vectorResX, vectorResY, vectorResZ;
    vectorResX = matrixCholesky.solve(vectorX);
    vectorResY = matrixCholesky.solve(vectorY);
    vectorResZ = matrixCholesky.solve(vectorZ);
    //得到新的标架
    for (int i = 0; i < m_vecAllVertex.size(); i++)
    {
        Eigen::Matrix3f matrixSelf;
        pVERTEX pVertex = m_vecAllVertex.at(i);
        float x1, x2, x3, y1, y2, y3, z1, z2, z3;
        x1 = vectorResX[i * 3];
        x2 = vectorResX[i * 3 + 1];
        x3 = vectorResX[i * 3 + 2];

        y1 = vectorResY[i * 3];
        y2 = vectorResY[i * 3 + 1];
        y3 = vectorResY[i * 3 + 2];

        z1 = vectorResZ[i * 3];
        z2 = vectorResZ[i * 3 + 1];
        z3 = vectorResZ[i * 3 + 2];

        pVertex->E1 = osg::Vec3(x1, x2, x3);
        pVertex->E2 = osg::Vec3(y1, y2, y3);
        pVertex->N = osg::Vec3(z1, z2, z3);

        //新的拉普拉斯坐标
        pVertex->lplsPos = (pVertex->E1 * pVertex->relativeX) + (pVertex->E2 * pVertex->relativeY) + (pVertex->N * pVertex->relativeZ);
    }
}

　　构建拉普拉斯矩阵

void mainNode::InitLpls()
{
    int vertexNumber = m_vecAllVertex.size();
    //计算顶点一阶临接顶点的权值,方式一
    for (int i = 0; i < vertexNumber; i++)
    {
        pVERTEX pVertex = m_vecAllVertex.at(i);
        int neighborNumber = pVertex->vecNeighborVertex.size();
        for (int j = 0; j < neighborNumber; j++)
        {
            pVERTEX pNeighbor = pVertex->vecNeighborVertex.at(j);
            float weight = float(1) / float(neighborNumber);
            pVertex->mapWeightForOther.insert(std::pair<int, float>(pNeighbor->id, weight) );
            pVertex->fTotalWeight = 1.0;
        }
    }

    /*
    //构建拉普拉斯矩阵权值，方式二
    for (int i = 0; i < vertexNumber; i++)
    {
        pVERTEX pVertex = m_vecAllVertex.at(i);
        float totalWeight = 0.0;
        for (int j = 0; j < pVertex->vecNeighborEdge.size(); j++)
        {
            pEDGE pEdge = pVertex->vecNeighborEdge.at(j);
            pVERTEX pA = pEdge->pA;
            pVERTEX pB = pEdge->pB;

            pVERTEX pTarget;
            if (pA->id == pVertex->id)
                pTarget = pB;
            else
                pTarget = pA;

            std::vector<pTRIANGLE> vecTri = pEdge->vecNeighborTri;
            pVERTEX pC = NULL;
            float weight = 0.0;
            for (int k = 0; k < vecTri.size(); k++)
            {
                pTRIANGLE pTri = vecTri.at(k);
                pVERTEX p1 = pTri->pA;
                pVERTEX p2 = pTri->pB;
                pVERTEX p3 = pTri->pC;
                if ((pA->id == p1->id && pB->id == p2->id) || (pA->id == p2->id && pB->id == p1->id))
                {
                    pC = p3;
                }
                else if ((pA->id == p1->id && pB->id == p3->id) || (pA->id == p3->id && pB->id == p1->id))
                {
                    pC = p2;
                }
                else if ((pA->id == p2->id && pB->id == p3->id) || (pA->id == p3->id && pB->id == p2->id))
                {
                    pC = p1;
                }
                //开始求取权值
                float cotAngle = 0.0;
                GetCotAngle(pA->pos, pB->pos, pC->pos, cotAngle);
                weight += cotAngle;
            }
            weight /= 2.0;
            pVertex->mapWeightForOther.insert(std::pair<int, float>(pTarget->id, weight) );
            totalWeight += weight;
        }
        pVertex->fTotalWeight = totalWeight;
    }
    */
    //计算拉普拉斯坐标
    for (int i = 0; i < vertexNumber; i++)
    {
        pVERTEX pVertex = m_vecAllVertex.at(i);
        osg::Vec3 pos = pVertex->pos;
        pos = pos * pVertex->fTotalWeight;
        osg::Vec3 otherPos = osg::Vec3(0.0, 0.0, 0.0);
        for (int j = 0; j < pVertex->vecNeighborVertex.size(); j++)
        {
            pVERTEX pNeihbor = pVertex->vecNeighborVertex.at(j);
            std::map<int, float>::iterator itor = pVertex->mapWeightForOther.find(pNeihbor->id);
            float weight = itor->second;
            otherPos += pNeihbor->pos * weight;
        }
        pVertex->lplsPos = pos - otherPos;
    }
    
    int count = 0;
    std::vector<int> beginNumber(vertexNumber);
    for (int i = 0; i < vertexNumber; i++)
    {
        beginNumber[i] = count;
        count += m_vecAllVertex[i]->vecNeighborVertex.size() + 1;
    }

    std::vector<Eigen::Triplet<float> > vectorTriplet(count);
    for (int i = 0; i < vertexNumber; i++)
    {
        pVERTEX pVertex = m_vecAllVertex.at(i);
        //原始拉普拉斯矩阵
        vectorTriplet[beginNumber[i]] = Eigen::Triplet<float>(i, i, pVertex->fTotalWeight);
        int j = 0;
        std::map<int, float>::iterator itor;
        for(itor = pVertex->mapWeightForOther.begin(); itor != pVertex->mapWeightForOther.end(); itor++)
        {
            int neighborID = itor->first;
            float weight = itor->second;
            vectorTriplet[beginNumber[i] + j + 1] = Eigen::Triplet<float>(i, neighborID, -weight);
            j++;
        }
    }

    //头一圈和顶一圈
    for (int i = 0; i < m_iAroundNumber * 2; i++)
    {
        float weight = 1.0;
        pVERTEX pVertex;
        if (i < m_iAroundNumber)
        {
            pVertex = m_vecAllVertex.at(i);
        }
        else
        {
            pVertex = m_vecAllVertex.at(i + m_iAroundNumber * 14);
        }

        int row = i + vertexNumber;
        vectorTriplet.push_back(Eigen::Triplet<float>(row, pVertex->id, weight));
    }
    
    m_Matrix.resize(vertexNumber + m_iAroundNumber * 2, vertexNumber);
    //m_Matrix.resize(vertexNumber, vertexNumber);
    m_Matrix.setFromTriplets(vectorTriplet.begin(), vectorTriplet.end());
    //std::cout << m_Matrix << std::endl;
}

　　根据新的拉普拉斯坐标求取新的顶点坐标

void mainNode::CalculateNewMatrixLpls()
{
    Eigen::SparseMatrix<float> Matrix = m_Matrix;

    Eigen::SparseMatrix<float> MatrixTranspose = Matrix.transpose();
    Eigen::SparseMatrix<float> MatrixLpls = MatrixTranspose * Matrix;

    Eigen::VectorXf targetX, targetY, targetZ;
    int vertexNumber = m_vecAllVertex.size();

    targetX.resize(vertexNumber + m_iAroundNumber * 2);
    targetY.resize(vertexNumber + m_iAroundNumber * 2);
    targetZ.resize(vertexNumber + m_iAroundNumber * 2);

    //方程式等号右边
    for (int i = 0; i < vertexNumber + m_iAroundNumber * 2; i++)
    {
        if (i < vertexNumber)
        {
            targetX[i] = m_vecAllVertex.at(i)->lplsPos[0];
            targetY[i] = m_vecAllVertex.at(i)->lplsPos[1];
            targetZ[i] = m_vecAllVertex.at(i)->lplsPos[2];
        }
        else if (i < vertexNumber + m_iAroundNumber)
        {
            //第一层的顶点坐标分量
            targetX[i] = m_vecAllVertex.at(i - vertexNumber)->pos.x();
            targetY[i] = m_vecAllVertex.at(i - vertexNumber)->pos.y();
            targetZ[i] = m_vecAllVertex.at(i - vertexNumber)->pos.z();
        }
        else
        {
            //最高层的顶点坐标分量
            targetX[i] = m_vecAllVertex.at((i - (vertexNumber + m_iAroundNumber) + (vertexNumber - m_iAroundNumber)))->pos.x();
            targetY[i] = m_vecAllVertex.at((i - (vertexNumber + m_iAroundNumber) + (vertexNumber - m_iAroundNumber)))->pos.y();
            targetZ[i] = m_vecAllVertex.at((i - (vertexNumber + m_iAroundNumber) + (vertexNumber - m_iAroundNumber)))->pos.z();
        }
    }
    
    Eigen::SimplicialCholesky<Eigen::SparseMatrix<float> > MatrixCholesky(MatrixLpls);
    Eigen::VectorXf resX, resY, resZ;
    resX = MatrixTranspose * targetX;
    resY = MatrixTranspose * targetY;
    resZ = MatrixTranspose * targetZ;

    Eigen::VectorXf X, Y, Z;
    X = MatrixCholesky.solve(resX);
    //std::cout << X << std::endl;
    Y = MatrixCholesky.solve(resY);
    //std::cout << Y << std::endl;
    Z = MatrixCholesky.solve(resZ);
    //std::cout << Z << std::endl;
    for (int i = 0; i < m_vecAllVertex.size(); i++)
    {
        pVERTEX pVertex = m_vecAllVertex.at(i);
        float x, y, z;
        x = X[i];
        y = Y[i];
        z = Z[i];

        pVertex->pos = osg::Vec3(X[i], Y[i], Z[i]);
    }
}

　　参考文献：

　　Linear Rotation-invariant Coordinates for Meshes

　　Laplacian-Surface-Editing

　　http://blog.csdn.net/hjimce/article/details/46415435

转载于:https://www.cnblogs.com/TooManyWayToBe/p/8465470.html