验证平稳性 - 走看看

2019独角兽企业重金招聘Python工程师标准>>>

以Nile序列拟合ARIMA模型为案例分析

验证序列的平稳性

验证平稳性的思路

1、平稳性一般通过时序图直观判断，或者通过ADF(Augmented Dickey-Fuller)统计检验来验证平稳性假定

a1、R中 tseries 包中的 adf.test() 可用来做 ADF检验，语句为 adf.test(ts)，ts为检验的序列，如过结果显著，则认为序列满足平稳性

2、如果方差不是常数，则需要数据做变换

3、如有存在趋势项，则需要对其进行差分

a、通过绘制时序图观察到各观测年间的方差似乎是稳定的，因此无需做数据变换

b、貌似有趋势项，所以进行ADF检验，差分，然后再ADF检验

> library(forecast)
> library(tseries)
> par(mfrow=c(2,1)) #绘制2*1布局的图
> plot(Nile) #绘制时序图观察是否平稳，各年间的方差似乎稳定，因此无需对数据做变换

> adf.test(Nile) #利用adf.test进行验证平稳性，p value >0.05，不显著，不平稳，所以需要进行差分

	Augmented Dickey-Fuller Test

data:  Nile
Dickey-Fuller = -3.3657, Lag order = 4, p-value = 0.0642
alternative hypothesis: stationary


> ndiffs(Nile)  #froecast包中的ndiffs找出最有的d（差分次数）
[1] 1
> dNile <- diff(Nile,1)# diff(ts,differences=d)其中d对时序ts的差分次数，默认d=1，可不写
> plot(dNile)
> adf.test(dNile)      #再用adf.test()进行平稳性验证

	Augmented Dickey-Fuller Test

data:  dNile
Dickey-Fuller = -6.5924, Lag order = 4, p-value = 0.01  #p value <0.05表示显著，表示平稳
alternative hypothesis: stationary

Warning message:
In adf.test(dNile) : p-value smaller than printed p-value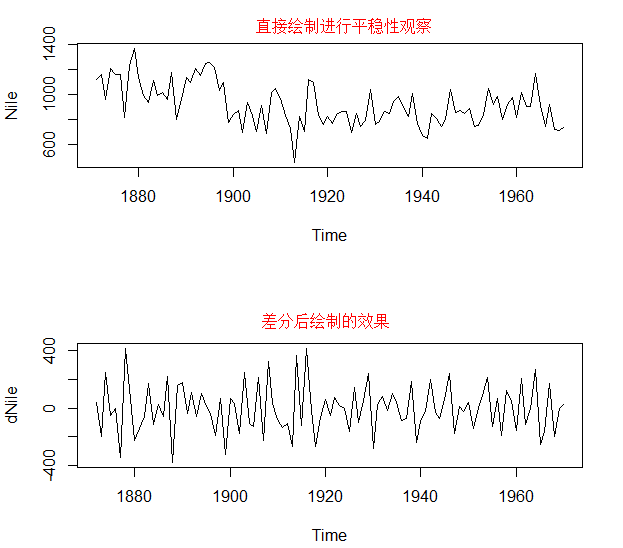

原始序列差分一次（函数默认一阶滞后项，即lag=1）并存储在dNile中，如上图差分后的序列的折线图，显然比原始序列更平稳，对差分后的序列做ADF检验，结果显示显著，说明序列是平稳的，

可继续下一步选择模型