【1】【leetcode-5】最长回文子串

给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。

示例 1：

输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。
示例 2：

输入: "cbbd"
输出: "bb"

链接：https://leetcode-cn.com/problems/longest-palindromic-substring

解法 1: 暴力破解

暴力求解，列举所有的子串，判断是否为回文串，保存最长的回文串。

时间复杂度：两层 for 循环 O(n²）O(n²），for 循环里边判断是否为回文 O(n）O(n），所以时间复杂度为 O(n³）O(n³）。

空间复杂度：O(1）O(1），常数个变量。

我的解法：超时，加了break后勉强AC

class Solution {
    public String longestPalindrome(String s) {
        String max = "";
        for (int i=0;i<s.length();i++) {
            for (int j=0;j<=i;j++) {
                if (isPalindrome(s.substring(j,i+1))) { //substring endindex 结尾处索引（不包括）
                    if (s.substring(j,i+1).length() > max.length()) {
                        max = s.substring(j,i+1);
                    }
                    break;
                }
            }
        }
        return max;
    }
    public boolean isPalindrome(String s) {
        boolean flag = true;
        for (int i=0;i<s.length()/2;i++) {
            if (s.charAt(i) != s.charAt(s.length()-i-1)) {
                flag = false;
                break;
            }
        }
        return flag;
    }
}

解法 2: 动态规划（重点）
解法一的暴力解法时间复杂度太高，在 leetCode 上并不能 AC。我们可以考虑，去掉一些暴力解法中重复的判断。我们可以基于下边的发现，进行改进。

时间复杂度：两层循环 O(n²）O(n²）。去掉了判断是否回文串的那层循环，改为用dp数组空间换时间

空间复杂度：用二维数组 PP 保存每个子串的情况 O(n²)O(n²)。

首先定义P(i，j）。

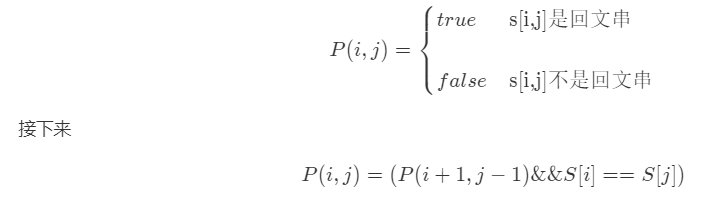
所以如果我们想知道 P（i,j）P（i,j）的情况，不需要调用判断回文串的函数了，只需要知道 P（i + 1，j - 1）P（i+1，j−1）的情况就可以了，这样时间复杂度就少了 O(n)O(n)。因此我们可以用动态规划的方法，空间换时间，把已经求出的 P（i，j）P（i，j）存储起来。

 

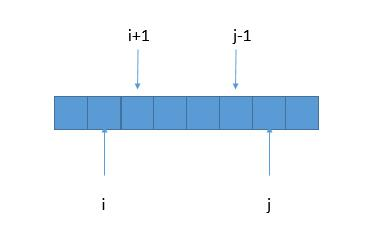
如果 S[i+1,j-1]S[i+1,j−1] 是回文串，那么只要 S[ i ]S[i] == $S[ j ] $，就可以确定 S[i,j]S[i,j]也是回文串了。

求 长度为 11 和长度为 22 的 P(i,j)P(i,j) 时不能用上边的公式，因为我们代入公式后会遇到 P[i][j]P[i][j] 中 i > j 的情况，比如求 P[1][2]P[1][2] 的话，我们需要知道 P[1+1][2-1]=P[2][1]P[1+1][2−1]=P[2][1] ，而 P[2][1]P[2][1] 代表着 S[2,1]S[2,1] 是不是回文串，显然是不对的，所以我们需要单独判断。

所以我们先初始化长度是 11 的回文串的 P [ i , j ]P[i,j]，这样利用上边提出的公式 P(i,j)=(P(i+1,j-1)&&S[i]==S[j])P(i,j)=(P(i+1,j−1)&&S[i]==S[j])，然后两边向外各扩充一个字符，长度为 33 的，为 55 的，所有奇数长度的就都求出来了。

同理，初始化长度是 22 的回文串 P [ i , i + 1 ]P[i,i+1]，利用公式，长度为 44 的，66 的所有偶数长度的就都求出来了。

public String longestPalindrome(String s) {
    int length = s.length();
    boolean[][] P = new boolean[length][length];
    int maxLen = 0;
    String maxPal = "";
    for (int len = 1; len <= length; len++) //遍历所有的长度
        for (int start = 0; start < length; start++) {
            int end = start + len - 1;
            if (end >= length) //下标已经越界，结束本次循环
                break;
            P[start][end] = (len == 1 || len == 2 || P[start + 1][end - 1]) && s.charAt(start) == s.charAt(end); //长度为 1 和 2 的单独判断下
            if (P[start][end] && len > maxLen) {
                maxPal = s.substring(start, end + 1);
            }
        }
    return maxPal;
}

参考代码 2：

public class Solution {

    public String longestPalindrome(String s) {
        int len = s.length();
        if (len <= 1) {
            return s;
        }
        int longestPalindrome = 1;
        String longestPalindromeStr = s.substring(0, 1);
        boolean[][] dp = new boolean[len][len];
        // abcdedcba
        //   l   r
        // 如果 dp[l, r] = true 那么 dp[l + 1, r - 1] 也一定为 true
        // 关键在这里：[l + 1, r - 1] 一定至少有 2 个元素才有判断的必要
        // 因为如果 [l + 1, r - 1] 只有一个元素，不用判断，一定是回文串
        // 如果 [l + 1, r - 1] 表示的区间为空，不用判断，也一定是回文串
        // [l + 1, r - 1] 一定至少有 2 个元素 等价于 l + 1 < r - 1，即 r - l >  2

        // 写代码的时候这样写：如果 [l + 1, r - 1]  的元素小于等于 1 个，即 r - l <=  2 ，就不用做判断了

        // 因为只有 1 个字符的情况在最开始做了判断
        // 左边界一定要比右边界小，因此右边界从 1 开始
        for (int r = 1; r < len; r++) {
            for (int l = 0; l < r; l++) {
                // 区间应该慢慢放大
                // 状态转移方程：如果头尾字符相等并且中间也是回文
                // 在头尾字符相等的前提下，如果收缩以后不构成区间（最多只有 1 个元素），直接返回 True 即可
                // 否则要继续看收缩以后的区间的回文性
                // 重点理解 or 的短路性质在这里的作用
                if (s.charAt(l) == s.charAt(r) && (r - l <= 2 || dp[l + 1][r - 1])) {
                    dp[l][r] = true;
                    if (r - l + 1 > longestPalindrome) {
                        longestPalindrome = r - l + 1;
                        longestPalindromeStr = s.substring(l, r + 1);
                    }
                }
            }
        }
        return longestPalindromeStr;
    }
}

解法 4: 扩展中心

时间复杂度：O(n²）O(n²）。

空间复杂度：O(1）O(1）。

我们知道回文串一定是对称的，所以我们可以每次循环选择一个中心，进行左右扩展，判断左右字符是否相等即可。

 

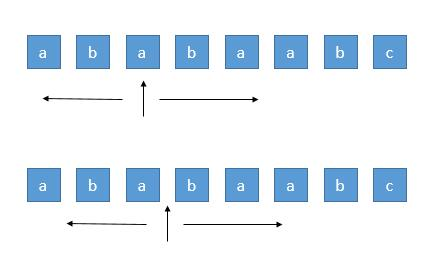
由于存在奇数的字符串和偶数的字符串，所以我们需要从一个字符开始扩展，或者从两个字符之间开始扩展，所以总共有 n+n-1 个中心。

public String longestPalindrome(String s) {
    if (s == null || s.length() < 1) return "";
    int start = 0, end = 0;
    for (int i = 0; i < s.length(); i++) {
        int len1 = expandAroundCenter(s, i, i);
        int len2 = expandAroundCenter(s, i, i + 1);
        int len = Math.max(len1, len2);
        if (len > end - start) {
            start = i - (len - 1) / 2;
            end = i + len / 2;
        }
    }
    return s.substring(start, end + 1);
}

private int expandAroundCenter(String s, int left, int right) {
    int L = left, R = right;
    while (L >= 0 && R < s.length() && s.charAt(L) == s.charAt(R)) {
        L--;
        R++;
    }
    return R - L - 1;
}