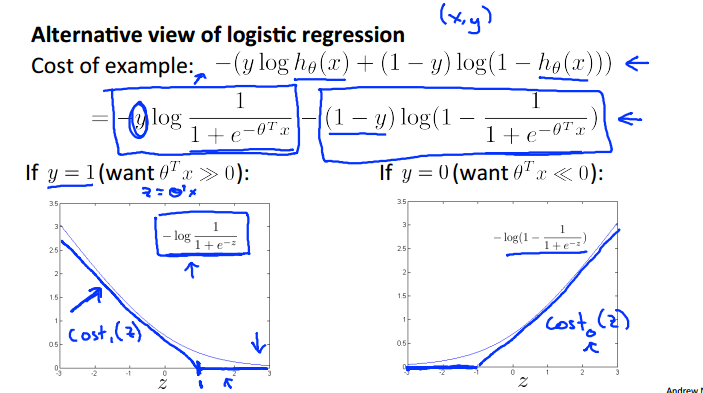
对于逻辑回归的新的view

支持向量机的函数设定为cost(),曲线和逻辑回归非常相似
A + lambda * B
c * A + B
只是设定不同的项不同的权重,两者可以转换的

large margin 的含义
正样本我们希望theta * x 大于 1 , 负样本则小于-1 ; 支持向量机的要求相对于逻辑回归更高,不仅仅是以0作为分界线。

SVM的决策边界,想让cost最小,则第一部分为0,也就是下面这两种情况:

决策边界是线性可分的:

C 设置的非常大的作用:
异常点的影响:圈圈中的个别叉或者叉中的个别圈 ,可能很轻易地改变了我们的决策边界。C设置地特别大则会避免这种情况。
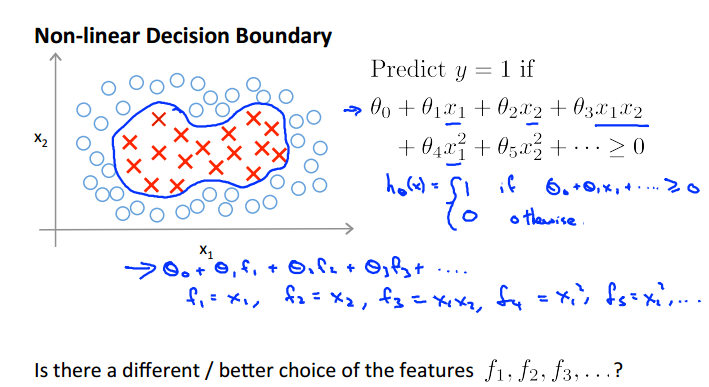
或者针对线性不可分的情况

kenerls
用f来表示x的幂次项
使用similarity(核函数)函数来计算x和随机选择的L点之间,这里选择的是高斯函数

如果x靠近l则高斯函数值为1,否则为0
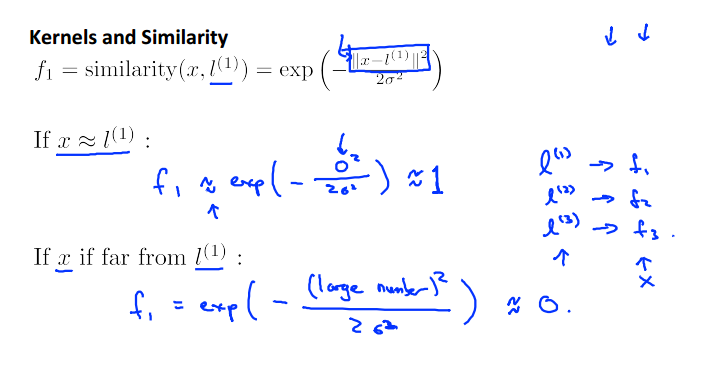
高斯函数的三位图像,方差的选择对于图像下降速度的影响,越大则下降地越慢(因为是分母嘛)
从图像中看出当两点接近时处于顶峰1,否则则随着距离的变远逐渐下降
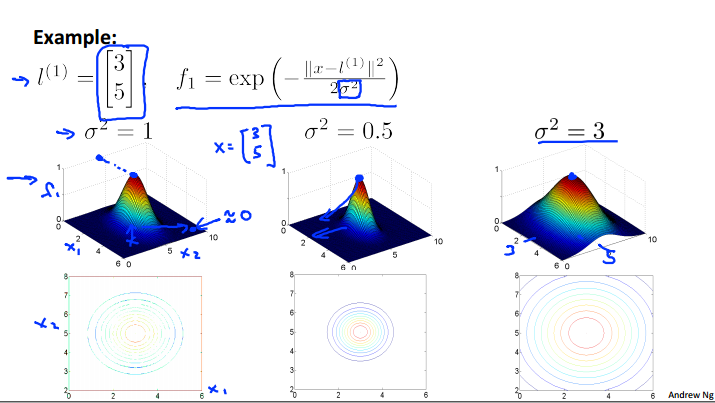
根据计算值的正负进行划分,这样就可以确定一个区域,即使不是线性可分也可确定一个非线性的区域

L:landmark的选择很简单啦其实就是每个训练集样本点:
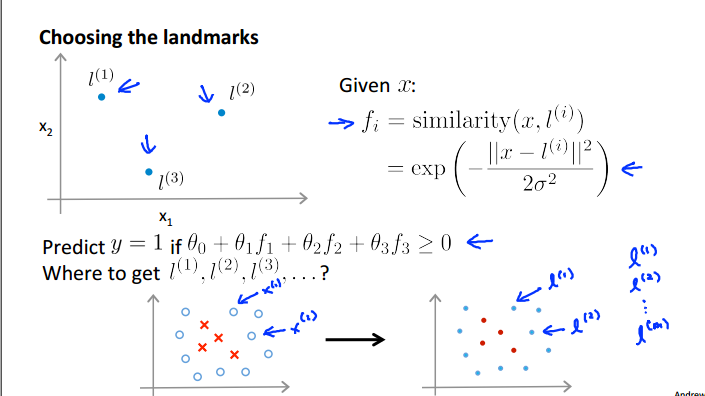
具体的操作过程:


参数的选择:

具体的实践
使用svm工具包来计算theta
需要明确指出:C参数和kernel函数的选择(默认为线性核函数)

这里注意一定要进行特征缩放

其他的和函数选择:满足默赛尔定理来正确地优化模型
多项式核函数
字符串核函数(输入为字符串)
...

多分类
许多svm包内建多分类工具
或者使用one vs all 的方法,计算完之后选择最大的

逻辑回归和svm的区别
1. 如果N很大,远大于M
使用逻辑回归或者线性的svm
2. 如果n 很小,M中等
使用高斯函数的svm
3. N很小,m很大
增加更多的特征,使用逻辑回归或者线性svm
神经网络对于这些都能适用,但是缺点是训练的很慢
