一. 思维导图
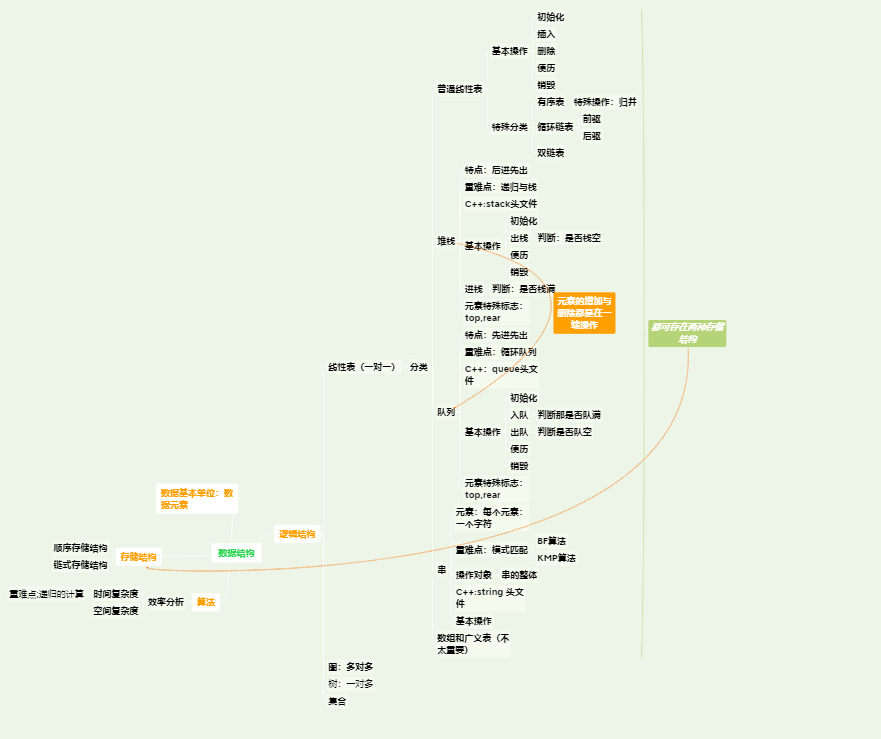
二. 重要概念的笔记
1,算法
- 评价算法的优劣:时间复杂度(T(n)=O(f(n)),n为问题规模)和空间复杂度(占用的额外存储空间随问题规模的变化)
- 栈的时间复杂度计算:1.分特殊情况和一般情况 2.将n拆成模块计算
2, 普通线性表
-
头插法与尾插法
注:头插法建立的表格元素顺序与输入元素顺序相反(可用于链表的逆序)
s->next=L->next; L->next=s;r->next=s; r=s; -
对于双向链表的插入操作
1.注意前驱与后驱的断开与连接
-
有序链表的归并(设有L1,L2,L3链表)
1.建立L1与L2中指向当前节点的指针,对L1与L2中的元素进行比较,并进行指针移动,复制节点到L3.若L1或L2中谁先为空,将L3的next指向剩下的链表中的当前指针
3,栈与队列
-
栈:后进先出,栈的插入与删除在栈顶,插入要判断是否栈满,删除要判断是否栈空
-
队列:先进先出,队列的插入在队尾,删除在队首,插入要判断是否队满,删除要判断是否队空
-
循环队列:队空:
r->rear==r->front; 队满:
(r->rear+1)%r->maxsize==r->front;
4,串
-
串的操作对象为串的整体
-
每个元素为一个字符
-
串的模式匹配:BF算法,KMP算法(next函数,nextval函数)
1.对于next函数的计算:当j从1开始,next[1]=0,next[j]=k,k-1=length(最大的前缀串与后缀串相等长度),其他情况next[j]=1;当j从0开始,next[0]=-1,next[1]=0,next[j]=k,k=length(最大的前缀串与后缀串相等长度)
2.对于nextval函数的计算:当j从1开始,nextval[1]=0;当j从0开始,nextval[j]=-1,
5,数组与广义表
-
矩阵为Amn中位于i行j列元素的地址,行优先:首地址+(im+j)k(k为单个元素所占的存储空间)
列优先:首地址+(jn+i)k(k为单个元素所占的存储空间)
三,疑难问题及解决方案
-
疑难问题:对于next数组和nextval数组的编程与理解(解决方案:实例分析及画图)
void get_next(string t, int len, int next[]) { int i = 0, j = 0;//j用来控制前缀串,i用来控制后缀串 next[0] = -1; while (i < len - 1) {//注意此时合法的最大下标为len-1 if (j = -1 || t[i] == t[j]) { i++; j++; next[i]=j;//对相等的最长的前缀串和后缀串长度+1 } else { j = next[j];//对j的回溯 } } }j 0 1 2 3 4 T[j] a c a c b Next[j] -1 0 0 1 2 -
设next[j]=k
-
a[0]=-1.i=1,j=0,若i与j相等,i++,j++,next[i]=j,即k=k+1;反之将j重新回到next[j]。若j为-1,对i进行移动i=i+1,j回到合法位置,相当于将寻找的最长的与前缀串相等的后缀串的起始位置向后移,前缀串的起始位置回到0;若此时我们得到的当前前缀串与后缀串比较相等,i++,j++,next[i]=j,即k=k+1;反之将j重新回到next[j]
-
void get_nextval(string t, int len, int next[])
{
int i = 0, j = 0;
next[0] = -1;
while (i < len - 1) {
if (j = -1 || t[i] == t[j]) {
i++;
j++;
if (t[i] != t[j]) {
nextval[i] = j;
}
else {
nextval[i] = nextval[j];//与next[j]求解中不同的部分
}
}
else
{
j = nextval[j];
}
}
}
| j | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| T[j] | a | a | a | b |
| Next[j] | -1 | 0 | 1 | 2 |
| Nextval[j] | -1 | -1 | -1 | 2 |
- nextval[j]=-1,假如我们的主串为s串:aaaaaab,下标用i表示,当比对到s[2]和t[2]时,i++,j++,当s[3]与t[3]相等时若将nextval[i]=nextval[j],且由于我们在主串与模式串匹配失配时,我们要将j回溯到nextval[j]与s[i]进行比较,则如例子若用next数组,需将s[3]与t[2]比较后,又与t[1]、t[0]比较,若直接将s[3]与t[0]比较,减少j回溯的次数.相当于标记模式串中相邻元素相等的关系