前言:打代码慢没关系,除非你不用心
一开始打了好多,但由于孙姓同学(gavensun.com)运行了一个恶意程序,然后本篇博文并没有保存,所以前言就说这么多
第一题,注意数据范围,不要吊儿郎当,原题也要打好
第二,三题(并查集求联通块:不要乱写,撞对垃圾样例并不一定对
2
道路
1000ms/128MB
M市有 n个城镇,同时有 m条道路(无向),城镇之间可以通过一条或多条道路到达。为了全面建设小
康社会,现要新建设一些道路,使得所有城镇之间两两可以互相到达。
请你计算出最少还需要建设多少条道路
输入格式:
第一行:两个正整数,分别是城镇数目 n(n<1000)和道路数目 m(m <= n * (n – 1)/2));随后的
m行对应 m条道路,每行给出两个正整数,分别是道路相连的两个城镇编号。城镇从 1到 N编号。
两个城市间可以有多条道路相通。
输出格式:一行一个整数。为最少需要建设的道路。
1 #include<cstdio> 2 #include<algorithm> 3 #define DEEEEEEEE 4 using namespace std; 5 const int MAXN = 1000+9; 6 const int MAXM = 500000+9; 7 8 int n,m,ans; 9 int fa[MAXN]; 10 bool visit[MAXN]; 11 12 int father(int x) { 13 if(x == fa[x]) return x; 14 return fa[x] = father(fa[x]); 15 } 16 17 int main() { 18 #ifdef DEEEEEEEE 19 freopen("b.in","r",stdin); 20 freopen("b.out","w",stdout); 21 #endif 22 scanf("%d%d",&n,&m); 23 for(int i = 1; i <= n; i++) fa[i] = i; 24 int fx,fy; 25 for(int i = 1, x, y; i <= m; i++) { 26 scanf("%d %d",&x,&y); 27 fx = father(x), fy = father(y); 28 fa[fx] =fy;//把道路的代表元素联通 29 } 30 for(int i = 1; i <= n; i++) { // 求联通块个数 31 if(!visit[father(i)]) {//先写father(i) 这才把fa[i]算出来 32 visit[fa[i]] = 1; 33 ans++; 34 } 35 } 36 printf("%d",ans-1);//ans个联通块,最少需要连ans-1条道路 37 return 0; 38 }
3.
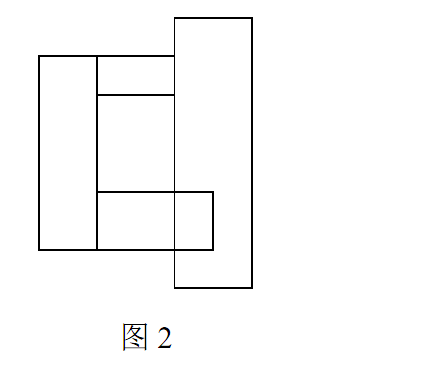
现在一个平面上画了 n 个矩形。每一个矩形的两边都与坐标轴相平行,且矩形定点的坐标均为整数。现定
义满足如下性质的图形为一个块:
1. 每一个矩形都是一个块;
2. 如果两个块有一段公共的部分,那么这两个块就会形成一个新的块,否则这两个块就是不同的。
示例:
图 1矩形形成了两个不同的块。图 2矩形形成了一个块。
找不同块的个数
#include<cstdio> #include<algorithm> #define DEEEEEEEE using namespace std; const int MAXN = 7000+9; int n,ans; int fa[MAXN]; bool visit[MAXN]; int father(int x) { if(x == fa[x]) return x; return fa[x] = father(fa[x]); } struct node{ int x1,y1,x2,y2; }e[MAXN]; bool judge(int x1,int y1, int x2, int y2, int x111, int y111, int x222, int y222) { //找关系的时候冷静一点,不要慌 if(x2<x111 || x1>x222 || y1>y222 || y2<y111 ) return 0;//没有一点相交 if( (x1==x222 || x2==x111) && (y1==y222 || y2==y111) ) return 0;//相交一点 return 1; } int main() { #ifdef DEEEEEEEE freopen("c.in","r",stdin); freopen("c.out","w",stdout); #endif scanf("%d",&n); for(int i = 1; i <= n; i++) fa[i] = i; int x1,y1,x2,y2,x111,y111,x222,y222; // 矩形1号 矩形2号 int f1,f2; for(int i = 1; i <= n; i++) { scanf("%d%d%d%d",&x1,&y1,&x2,&y2); e[i].x1 = x1, e[i].x2 = x2, e[i].y1 = y1, e[i].y2 = y2; for(int j = 1; j < i; j++) { x111 = e[j].x1 , y111 = e[j].y1 , x222 = e[j].x2 , y222 = e[j].y2 ; if(judge(x1,y1,x2,y2,x111,y111,x222,y222) ) { f1 = father(i), f2 = father(j); fa[f1] = f2; } } } for(int i = 1; i <= n; i++) { if(!visit[father(i)]) { visit[fa[i]] = 1; ans++; } } printf("%d",ans); return 0; }
第四题:分层图(仔细分析题目,不要看见那么多的条件就害怕
消失的 c题(c.cpp/c.in/c.out)
1000ms/128MB
题目描述
N 个虫洞,M 条单向跃迁路径。从一个虫洞沿跃迁路径到另一个虫洞需要消耗一定量的燃料和 1 单
位时间。虫洞有白洞和黑洞之分。设一条跃迁路径两端的 虫洞质量差为 delta。
1.从白洞跃迁到黑洞,消耗的燃料值减少 delta,若该条路径消耗的燃料值变为负数的话,取为 0。
2.从黑洞跃迁到白洞,消耗的燃料值增加 delta。
3.路径两端均为黑洞或白洞,消耗的燃料值不变化。
每过 1 单位时间黑洞变为白洞,白洞变为黑洞。
在飞行过程中,可以选择在一个虫洞停留 1 个单位时间,如果当前为白洞,则不消耗燃料,否则消
耗 s[i]的燃料。现在请你求出从 虫洞 1 到 N 最少的燃料消耗,保证一定存在 1 到 N 的路线。
输入格式第 1 行:2 个正整数 N,M
第 2 行:N 个整数,第 i 个为 0 表示虫洞 i 开始时为白洞,1 表示黑洞。
第 3 行:N 个整数,第 i 个数表示虫洞 i 的质量 w[i]。
第 4 行:N 个整数,第 i 个数表示在虫洞 i 停留消耗的燃料 s[i]。第 5..第 M+4 行:每行 3 个整数,u,v,k,表示在没有影响的情况下,从虫洞 u到虫洞 v 需要消耗燃料 k。
输出格式
一个整数,表示最少的燃料消耗。
样例输入
4 5
1 0 1 0
10 10 100 10
5 20 15 10
1 2 30
2 3 40
1 3 20
1 4 200
3 4 200
样例输出
130
数据范围
对于 30%的数据: 1<=N<=100,1<=M<=500
对于 60%的数据: 1<=N<=1000,1<=M<=5000
对于 100%的数据: 1<=N<=5000,1<=M<=30000
其中 20%的数据为 1<=N<=3000 的链
1<=u,v<=N, 1<=k,w[i],s[i]<=200
样例说明
按照 1->3->4 的路线。
1 #include<cstdio> 2 #include<algorithm> 3 #include<queue> 4 #define DEEEEEEEE 5 using namespace std; 6 const int MAXN = 10000+99; 7 const int MAXM = 90000+99; 8 const int INF = 2147000047; 9 10 int n,m,cnt,head[MAXN],dis[MAXN],vis[MAXN]; 11 int wb[MAXN];//wb[i] 为0表示i开始为白洞,1表示黑洞 12 int w[MAXN];//i的质量 13 int s[MAXN];//停留时的消耗能量 14 15 struct edge{ 16 int next,y,val; 17 }e[MAXM]; 18 19 void add_edge(int x, int y, int val) { 20 e[++cnt].y = y; 21 e[cnt].val = val; 22 e[cnt].next = head[x]; 23 head[x] = cnt; 24 } 25 26 struct node{ 27 int id,dis; 28 node (int id = 0, int dis = 0) : id(id) , dis(dis){} 29 bool operator < (const node &xx) const { 30 return dis > xx.dis ; 31 } 32 }; 33 priority_queue <node> q; 34 35 int abs(int x, int y) { 36 if(x > y) return x - y; 37 else return y - x; 38 } 39 40 void init() ; 41 int main() { 42 #ifdef DEEEEEEEE 43 freopen("c.in","r",stdin); 44 freopen("c.out","w",stdout); 45 #endif 46 init(); 47 for(int i = 1; i <= n*2; i++) dis[i] = INF; 48 dis[1] = 0; 49 q.push(node(1,0)) ; 50 while(!q.empty() ) { 51 node tmp = q.top() ; 52 q.pop(); 53 int now = tmp.id ; 54 if(vis[now]) continue; 55 vis[now] = 1; 56 for(int i = head[now]; i; i = e[i].next ) { 57 int y = e[i].y; 58 int dalta = abs(w[now] , w[y]); 59 if(wb[now]==0 && wb[y]==1) dalta = max(0, e[i].val - dalta); 60 else if(wb[now]==1 && wb[y]==0) dalta = e[i].val + dalta; 61 else dalta = e[i].val ; 62 63 if(y > n) y -= n; 64 else y += n;//注意换图 65 66 if(dis[y] > tmp.dis + dalta) { 67 dis[y] = tmp.dis + dalta; 68 q.push(node(y,dis[y])); 69 } 70 } 71 //下面考虑的是停留的情况 72 int t = 0, nn = now; 73 if(wb[now] == 1) t = s[now];//t是真正停留花费的能量 74 if(nn > n) nn -= n; 75 else nn += n;//依然是换图 76 if(dis[nn] > tmp.dis + t) { 77 dis[nn] = tmp.dis + t; 78 q.push(node(nn,dis[nn])); 79 } 80 } 81 printf("%d",min(dis[n], dis[n+n]));//比较两图之后再输出 82 return 0; 83 } 84 85 void init() { 86 scanf("%d%d",&n,&m); 87 for(int i = 1; i <= n; i++) scanf("%d",&wb[i]) , wb[i+n] = wb[i] ^ 1; 88 for(int i = 1; i <= n; i++) scanf("%d",&w[i]) , w[i+n] = w[i]; 89 for(int i = 1; i <= n; i++) scanf("%d",&s[i]) , s[i+n] = s[i]; 90 int x,y,val; 91 for(int i = 1; i <= m; i++) { 92 scanf("%d%d%d",&x,&y,&val); 93 add_edge(x,y,val); 94 add_edge(x+n,y+n,val); 95 /*不能再无脑地将上下两个图联通,因为还要考虑当前点是白洞,可能不耗能 96 这里的两个图只是黑白颠倒的,因为每次跃迁时都会花费 1 单位时间,所以每次都要换图*/ 97 } 98 }
下面是我们亲爱的庆鸽鸽的SPFA版,特意再次发出,表示感谢, 同时,缅怀一下我第一个学会的最短路算法——SPFA(本人一开始认为floyd太麻烦,没记...
#include <cstdio> #include <queue> #include <algorithm> #include <cstring> #define MAXN 11111 #define MAXM 111111 int n, m, cnt; int p[MAXN], w[MAXN], s[MAXN]; int vis[MAXN], dis[MAXN], head[MAXN]; std::queue <int> q; struct edge { int y, val, next; edge(int y = 0, int val = 0, int next = 0) : y(y), val(val), next(next) {} }e[MAXM]; inline void add_edge(int x, int y, int z) { e[++cnt] = edge(y, z, head[x]); head[x] = cnt; } int abs(int x) { return x >= 0 ? x : -x; } int main() { freopen("c.in", "r", stdin); freopen("c.out", "w", stdout); scanf("%d%d", &n, &m); for(int i = 1; i <= n; i++) scanf("%d", &p[i]), p[i + n] = p[i] ^ 1; for(int i = 1; i <= n; i++) scanf("%d", &w[i]), w[i + n] = w[i]; for(int i = 1; i <= n; i++) scanf("%d", &s[i]), s[i + n] = s[i]; for(int i = 1, x, y, z; i <= m; i++) { scanf("%d%d%d", &x, &y, &z); add_edge(x, y, z); add_edge(x + n, y + n, z); } for(int i = 0; i <= n * 2; i++) dis[i] = -1; q.push(1); vis[1] = 1; dis[1] = 0; while(!q.empty()) { int now = q.front(); q.pop(); vis[now] = 0; for(int i = head[now]; i; i = e[i].next) { int nn = e[i].y, tmpn = nn; int del = abs(w[now] - w[nn]); if(nn > n) nn -= n;///////////////// else nn += n;/////////////// if(!p[now] && p[tmpn]) del = std::max(0, e[i].val - del); else if(p[now] && !p[tmpn]) del = e[i].val + del; else del = e[i].val; if(dis[nn] == - 1 || dis[nn] > dis[now] + del) { dis[nn] = dis[now] + del; if(!vis[nn]) { vis[nn] = 1; q.push(nn); } } } int t = 0, nn = now; if(p[now]) t = s[now]; if(nn > n) nn -= n; else nn += n; if(dis[nn] == - 1 || dis[nn] > dis[now] + t) { dis[nn] = dis[now] + t; if(!vis[nn]) { vis[nn] = 1; q.push(nn); } } } printf("%d ", std::min(dis[n], dis[n + n])); return 0; }
第五题:DP( 好好学习,好好做人,不要好高骛远,请脚踏实地
杆子(e.cpp/e.in/e.out)
1000ms/256MB
题目描述
现在有 n个高矮不同的杆子,第 i个杆子高度为 i。
有许多的方案能够将这 n个杆子排成一排。
从最左边看和从最右边看这一排 n个杆子分别能看到一定数目的杆子(高的杆子会挡住矮的杆子)。
现在问从左端看能看见 L根,同时从右端看能看见 R根的方案数有多少
%1000000007
输入格式
一个 n
之后 n个数为杆子的高度
输出格式
方案数样例输入
4 1 2(高度应该都是1 ~ n)
样例输出
2
样例解释
4 1 2 3
4 2 1 3
对于 40 %的数据 N <= 11;
对于 90 % 的数据 N <= 400,L,R <= N
对于 100 % 的数据 N <= 600
1 #include<cstdio> 2 #include<iostream> 3 #include<algorithm> 4 //#define DEEEEEEEE 5 using namespace std; 6 const int MOD = 1000000007 ; 7 const int MAXN = 600+9; 8 9 int n,L,R; 10 int hi[MAXN]; 11 unsigned long long d[2][MAXN][MAXN]; 12 /*d[MAXN][MAXN][MAXN] : d[i][j][k] 表示 前i个杆子摆放成: 从左边看见j个, 从右边看见k个 的方案数 13 我们不妨每次认为放的都是最矮的(矮和高放的顺序是随意的,因为总要放满n个杆子,这样好写状态转移罢了) 14 有: d[i][j][k] = d[i-1][j-1][k] + d[i-1][j][k-1] + d[i-1][j][k]*(i-2) / 第i个杆子放在最左边的方案数 + 放在最右边的方案数 + 放在中间的方案数 15 注意:内存会炸掉 !! 仔细观察后,发现该 状态转移方程 只用到了当前状态 和 上一状态 这两个状态,所以可以用滚动数组优化 16 (细节见代码,好像没有什么细节的...只需想好状态转移 17 */ 18 19 inline unsigned int g(int x) {return x-( (x>>1)<<1);} // 实际上就是一个 i % 2 ,只是比较快 20 21 int main() { 22 #ifdef DEEEEEEEE 23 freopen("e.in","r",stdin); 24 freopen("e.out","w",stdout); 25 #endif 26 scanf("%d%d%d",&n,&L,&R); 27 d[1][1][1] = 1;//初始化 28 for(int i = 2; i <= n; i++) 29 for(int j = 1; j <= i; j++) 30 for(int k = 1; k <= i; k++) //这里都是前i个 31 d[g(i)][j][k] = ( d[g(i-1)][j-1][k] + d[g(i-1)][j][k-1] + d[g(i-1)][j][k]*(i-2) )% MOD; 32 33 cout << d[g(n)][L][R]; 34 return 0; 35 }