KMP算法略解

前言
本文是我对 KMP 算法的临时理解， 用于使我不怀疑 KMP 算法的正确性，用着放心。

---

---

如图 (1) , 长串与短串进行匹配暴力对齐匹配时，在红叉号处失配， 长串的子串蓝串和短串的前缀黄串相等。

如图 (2)， 试图利用已有信息（黄串等于蓝串）， 来快速寻找短串串头下一次应该对齐长串的哪个位置， 这个位置被描述为 “下一个可能会在那匹配成功的位置”。

如图 (3)， 假设自前日败北后，找到了第一个使得绿线划分出的蓝串与黄串的两部分相等的位置。
由于没有长串在绿线右边的信息， 所以此时无法断定此位置的匹配是否会成功， 即此位置就是要找的 “下一个可能会在那匹配成功的位置”。
显然， 如果绿线划分出的黄串与蓝串不全相等， 那么此位置一定会失配。

如图 (4)， 绿线的印记留在黄串与蓝串上， 对齐黄串与蓝串，观察。
发现只要找出黄串的 后缀等于前缀的最长长度 （值得注意的是， 这里的最长长度不应等于黄串的串长）即可以找到所谓 “下一个可能会在那匹配成功的位置”。

---

线性求 (next) 数组的方法

[今天的我是最强哒！ by;某莱伊or某路易or某鲁伊 ]

看图， 只可意会， 不可言传qwq（lazy boy）

---

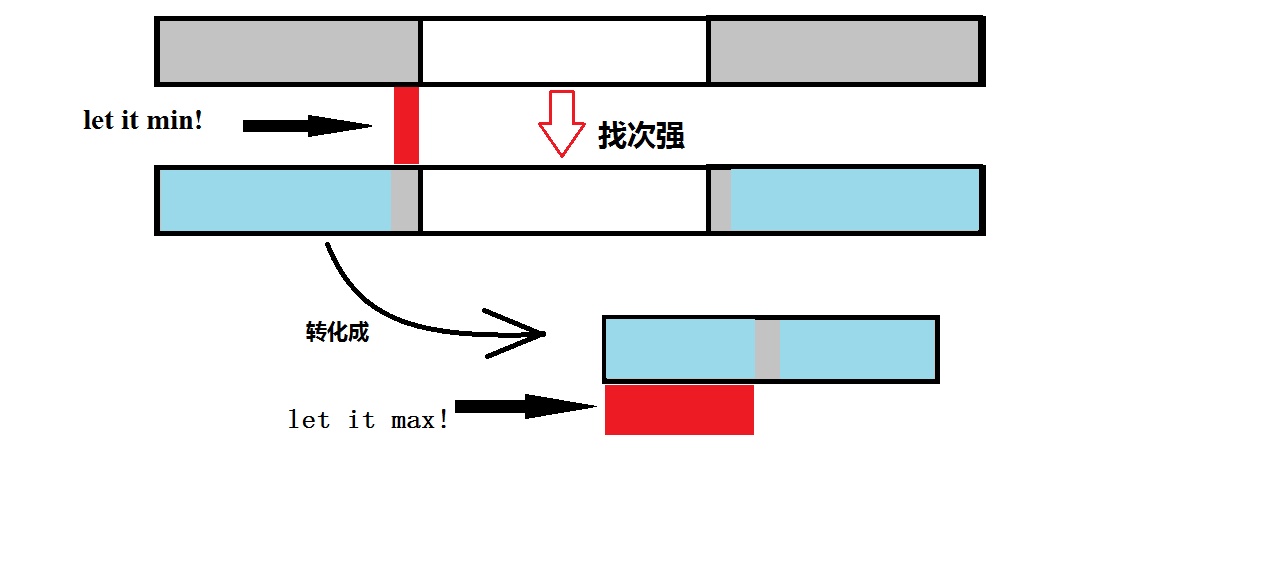
Luogu板子题AC代码

#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e6+15;

char s1[maxn], s2[maxn];
int len1, len2;
int nxt[maxn], f[maxn];

int main()
{
	scanf("%s%s", s1+1,s2+1);
	len1=strlen(s1+1), len2=strlen(s2+1);
	for(int i=2,j=0;i<=len2;++i) {
		//从2开始是为了避免 nxt[i]=i的尴尬情况
		//为甚么？写下nxt[i]=i的必要条件看看 
		while(j&&s2[j+1]!=s2[i]) j=nxt[j];
		if(s2[j+1]==s2[i]) ++j;
		nxt[i]=j;
	}
	for(int i=1,j=0;i<=len1;++i) {
                //将短串的某个前缀的尾部与长串的某个子串的尾部对齐~~~
                //此时短串的这个前缀与长串的这个子串是匹配成功的qwq
		while(j&&(j==len2||s2[j+1]!=s1[i])) j=nxt[j];
		if(s2[j+1]==s1[i]) ++j;
		f[i]=j;
	}
	for(int i=1;i<=len1;++i) if(f[i]==len2) cout<<i-len2+1<<'
';
	for(int i=1;i<=len2;++i) cout<<nxt[i]<<' ';
	return 0;
}