算法导论笔记 第三十章 多项式与快速傅里叶变化

引言

定义：

（多项式的）次数：一个多项式A(x)的最高次的非零系数是a_k ，则称A(x)的次数为k，记作degree(A)=k

次数界：任何严格大于多项式次数的整数都是该多项式的次数界

30.1 多项式的表示

两种表示形式：

1. 系数表示：就是我们一般常见的A(x)=Σa_kx^k形式
2. 点值表示：一个次数界为n的多项式A(x)的点值表达是由n个点值对组成的集合{(x₀,y₀), (x₁,y₁),…, (x_n-1,y_n-1)},使得对于k=0,1,2,..,n-1所有的x_k均不相同，y_k=A(x_k)

插值：从一个多项式的点值表达确定其系数表达

拉格朗日公式：在O（N²）的时间内计算A的所有系数

DFT：傅里叶变换

定理30.1：（插值唯一定理）n个点对且所有x_k都不相同的点值表达式，对应的次数界为n的系数表达式唯一。证明：利用范德蒙行列式

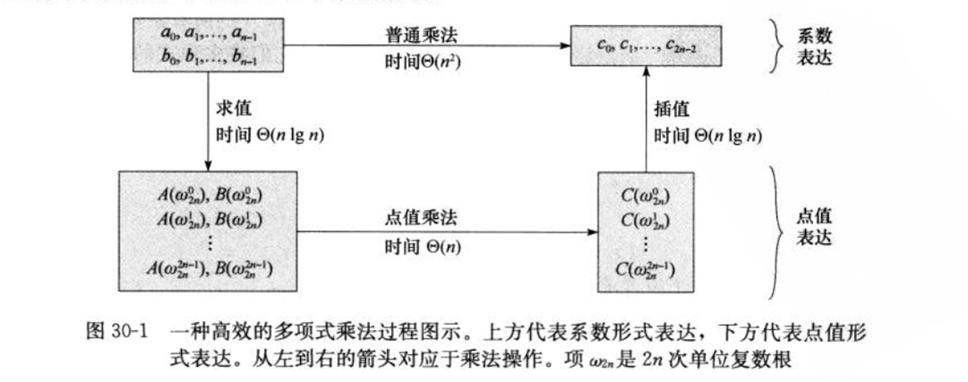
普通插值运算的时间复杂度为O(n²),此处我们使用了精心挑选的一些数据，使用单位复数根，可以在O(nlgn)的时间内完成插值和求值的运算。

30.2

定义：

单位复数根：满足wⁿ=1的复数w，利用负指数的定义，这些根是e^(2πi/n)×k。均匀的分布在以复平面空间为圆心的单位半径的圆周上。

主n次单位根：e^(2πi/n)，记作w_n，其他的n次单位复数根都是w_n的幂次。

 

引理：

消去引理：对于常数d>0，有(w_dn)^dk=(w_n)^k。证明：直接由定义得到

折半引理：对于任意偶数n>0有w_n^n/2=w₂=-1。证明：消去引理

求和引理：对于任意整数n≥1和不能被n整除的非负整数k，有：Σ_j=0^n-1(w_n^k)^j=0。证明：用实数里面我们熟知的等比数列求和法，交换分子多项式w系数的内外阶数

 

DFT（离散傅里叶变化）：

把n个单位复数根作为x向量带入多项式A(x)中求解y向量，其中y向量就是系数向量a的DFT，记作y=DFT_n(a)

 

FFT（快速傅里叶变化）：

利用复数单位根的特殊性质，在o(nlogn)的时间内计算出DFT_n(a)，此处假设n是2的整数次幂（其他情况也能有相同的时间复杂度，但具体操作此处不做要求）。

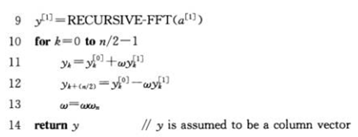
旋转因子：w^k_n

_p