题干在最后
首先承认这道题用了我很多的时间,作为一个动态规划入门者兼vj新手,这道题对我来讲是比较有难度的。
感想就是,设置判断条件时,一定要考虑全面,不要怕代码长;
然后就是,对于动态规划,不应只把他当作一种套路甚至是解体模版;这样的话,你就总是想“拿条件,套公式”,对于dp,这种思想是危险而又行不同的。
我觉得更应该把dp当作一种思想,解决、看待这类问题的一种角度,如果说对于dp题有套路,这个套路只能是dp的思想,而不应该包含代码之类的东西。
在做这道题的同时我就犯了上述错误,在重新看了一遍北大的《算法基础》关于递归的部分后,我基本独立的写出来了自己的ac代码。
网上有很多这道题的解析,但我觉得对入门者都不够友好,而且写的很杂乱,如果你也在入门dp,希望我的分享能对你有帮助。
入门者的dp问题分析:
在做dp问题时,可以先用递归的思想去考虑问题,先分解出整个求解过程中,其中一个完整的递归过程,然后考虑边界条件;
对于这道题,我把从某平板的一端落下,再左右移动到所在平板的左or右端作为一个“完整的递归过程”,如图:
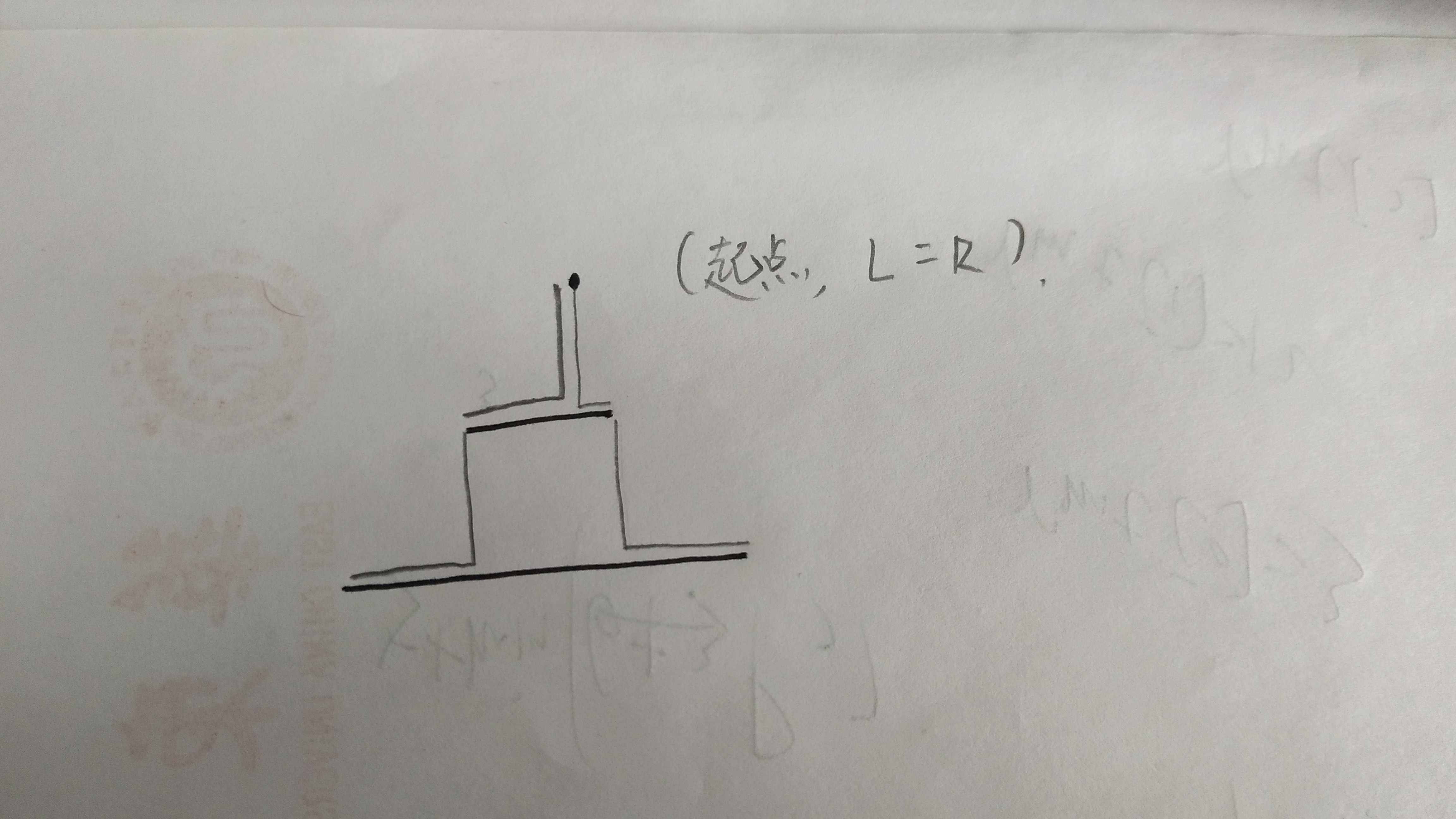
其中四条铅笔线都可以看作一个完整的递归过程,如果你还不明白的话:
铅笔线的起点到底部的最小路程,就等于铅笔线这条曲线的长度,加上终点到底部的最短路程;
对于小老鼠一开始的下落,这个递归过程也是适用的。
这里的递归,就是“归”到了“求一个点到底部的最短距离”这个问题上,也就是上面这句话的高亮部分。
左右端点下落情况非常相似,我们要分开求,最终比较的就是,小老鼠一开始下落时,从板子左边掉下去和从右边掉下去那个路程更短。
边界条件:如果点下方没有板子了,那就不再递归,而是返回点的高度(也就是点所在板子的高度)。
然后问题是,如何判断端点下面有没有板子呢?
这里,点的下方可能有板子,也可能没有板子,也可能有许多板子,很自然能能想到的办法是,我们将板子按高度排序,判断我们点所在的板子下方的那块板子,是不是在端点下方;这个判断就不难了,只需判断我们(小老鼠)所在板子的端点与下面那块板子的左右端点的关系就能得出结论。
再然后,当用递归的函数直接求解dp问题时,中间过程往往会出现,某一个问题重复多次求解的现象(不理解的同学可以看看北大《算法基础》慕课第四章第一节,讲的非常好),浪费了时间与空间资源,这时我们的策略是,把每一个求解过的问题都存起来,下一次要求这个问题时就直接使用结果了。
因此,根据我们所找出的递归过程的特点,我们从下往上求,这样上面的就可以用下面的板子端点的结果了;
一直求到最高点,那么最终结果就是左侧下落,和右侧下落,结果中的最小值了。
其中注意结构体排序的'>' '<'的结构体内的定义,这种方法非常简洁,应当记住。
代码如下:(代码放上去排版有点诡异,不过并不影响阅读)
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define maxn 1000+10
#define inf 100000000
int x,y,np,mh,lmt[maxn],rmt[maxn];
struct flat{
int l,r,h;
friend bool operator < (flat a,flat b){
return a.h<b.h;
}
}f[maxn];
int qiu_lmt(int b){ //从b板左端点落下的最短路程,结果存于lmt[b]
if(b==0){
lmt[b]=f[b].h;
// cout<<lmt[b]<<endl;
return 0;
}
int x=-1;
for(int i=b-1;i>=0;i--){
if(f[i].l<=f[b].l && f[i].r>=f[b].l) //左端点下面有板子吗
{x=i;break;}
}
if(x==-1) {
if(f[b].h<=mh)
{lmt[b]=f[b].h;
// cout<<lmt[b]<<endl;
}
else {
lmt[b]=inf;
// cout<<lmt[b]<<endl;
return 0;}
}
else if(f[b].h-f[x].h<=mh){
lmt[b]=f[b].h-f[x].h+min(f[b].l-f[x].l+lmt[x],f[x].r-f[b].l+rmt[x]);
// cout<<lmt[b]<<endl;
return 0;
}
else {
lmt[b]=inf;
// cout<<lmt[b]<<endl;
return 0;
}
}
int qiu_rmt(int b){ //从b板右端点落下的最短路程,结果存于rmt[b]
if(b==0){
rmt[b]=f[b].h;
// cout<<rmt[b]<<endl;
return 0;
}
int x=-1;
for(int i=b-1;i>=0;i--){
if(f[i].l<=f[b].r && f[i].r>=f[b].r) //右端点下面有板子吗
{ x=i;break; }
}
if(x==-1) {
if(f[b].h<=mh){rmt[b]=f[b].h;
// cout<<rmt[b]<<endl;
}else {
rmt[b]=inf;
// cout<<rmt[b]<<endl;
return 0;}
}
else if(f[b].h-f[x].h<=mh){
rmt[b]=f[b].h-f[x].h+min(f[b].r-f[x].l+lmt[x],f[x].r-f[b].r+rmt[x]);
// cout<<rmt[b]<<endl;return 0;
}
else {
rmt[b]=inf;
// cout<<rmt[b]<<endl;
return 0;
}
}
int mintime(){
for(int i=0;i<=np;i++){
qiu_lmt(i); //从下至上,求出每个端点到底部的最短距离
qiu_rmt(i); //结果与这俩函数先后次序无关
}
return rmt[np]>=lmt[np]?lmt[np]:rmt[np]; //求最小值
}
int main(){
freopen("in.txt","r",stdin);
int n;
while(scanf("%d",&n)==1){
while(n--){
scanf("%d%d%d%d",&np,&x,&y,&mh);
f[0].l=f[0].r=x;
f[0].h=y;
for(int i=1;i<=np;i++){
scanf("%d%d%d",&f[i].l,&f[i].r,&f[i].h);
}
sort(f,f+np+1); //升序
// cout<<f[0].h<<' '<<f[1].h<<' '<<f[2].h<<' '<<f[3].l<<' '<<f[3].r<<' '<<f[0].l<<' '<<f[0].r<<endl;
cout<<mintime()<<endl;
}
}
return 0;
}
题意:"Help Jimmy" 是在下图所示的场景上完成的游戏。
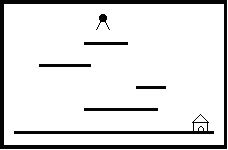
场景中包括多个长度和高度各不相同的平台。地面是最低的平台,高度为零,长度无限。
Jimmy老鼠在时刻0从高于所有平台的某处开始下落,它的下落速度始终为1米/秒。当Jimmy落到某个平台上时,游戏者选择让它向左还是向右跑,它跑动的速度也是1米/秒。当Jimmy跑到平台的边缘时,开始继续下落。Jimmy每次下落的高度不能超过MAX米,不然就会摔死,游戏也会结束。
设计一个程序,计算Jimmy到底地面时可能的最早时间。