反演变换学习笔记

定义:

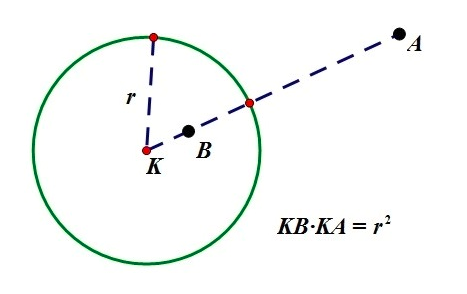
给定平面上一个反演中心(O)，给定反演半径(r)，对于平面上任意一个点(A),都可以找到一个点(A')，使得(OA*OA'=r^2)，称(A')为(A)关于(O)的反演点，以(O)为圆心(r)为半径的圆称为反演圆。(下图中圆K为反演圆，A和B互为反演点)

性质

• 过反演中心的直线反演后就是自身
• 不过反演中心的直线反演后时过反演中心的圆

• 不过反演中心的圆(A)反演后也是一个圆(A')， 当(A)与圆(O)相交时，(A′)也与圆(O)相交；当(A)与圆(O)外（内）切时，(A′)与圆(O)内（外）切；当(A)与圆(O)相离（内含）时，(A′)与圆(O)内含（相离）。

• 直线(A)与圆(O)相切，过不在圆上的一点(K)反演后圆(A')和圆(O')相切

模板

Point PtP(Point a,Point p,double r){//点到点
    Point v1=a-p;
    v1.stdd();
    double len=r*r/dist(a,p);
    return p+v1*len;
}
Circle CtC(Circle C,Point p,double r){//圆到圆
    Circle res;
    double t = dist(C.o,p);
    double x = r*r / (t - C.r);
    double y = r*r / (t + C.r);
    res.r = (x - y) / 2.0;
    double s = (x + y) / 2.0;
    res.o = p + (C.o - p) * (s / t);
    return res;
}
Circle LtC(Point a,Point b,Point p,double r){//直线到过反演点的圆
    double d=distLP(a,b,p);
    d=r*r/d;
    Circle c;
    c.r=d/2;
    Point v1;
    if(xmult(a,b,p)>0)
        v1=(a-b).Rotate(PI/2);
    else
        v1=(b-a).Rotate(PI/2);
    v1.stdd();
    c.o=p+v1*c.r;
    return c;
}