1.信息熵公式: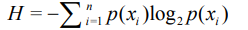
p(x)为某个特征的概率,介于0到1之间
2.基尼不纯度公式:
p(i)为某个特征的概率,介于0到1之间
3.假设某集合只有一个分类,该分类有相反的两个特征,那么
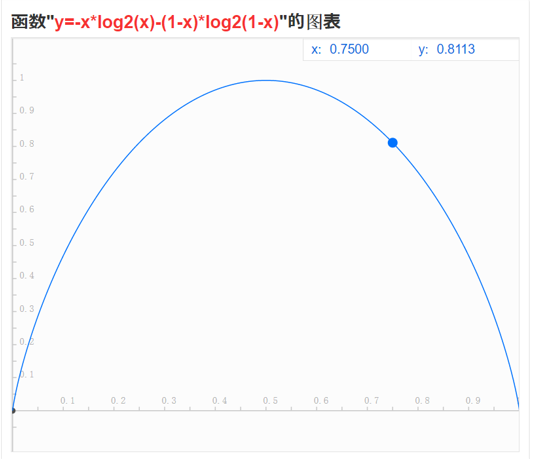
信息熵公式可以简化为-xlog2x-(1-x)log2(1-x),对应图像:
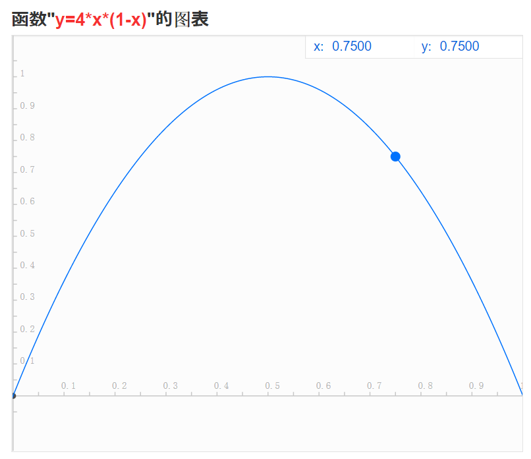
基尼不纯度公式可以简化为x(1-x),对应图像(为了方便对比乘以了4倍):
4.总结
1.可以看出两者的函数图非常接近,信息熵的两侧弧度稍微比基尼不纯度大一点。
2.在特征概率为0.5时信息量最大,特征概率为0或1时信息量为零。
3. 两者都可用于衡量系统混乱程度,y值越大,混乱程度越高,信息量也越大。