旅行者问题
【问题描述】
lahub是一个旅行者的粉丝,他想成为一个真正的旅行者,所以他计划开始一段旅行。lahub想去参观n个目的地(都在一条直道上)。lahub在起点开始他的旅行。第i个目的地和起点的距离为ai千米(ai为非负整数)。不存在两个目的地和起点的距离相同。
从第i个目的地走到第j个目的地所走的路程为 |ai-aj|千米。我们把参观n个目的地的顺序称作一次“旅行”。lahub可以参观他想要参观的任意顺序,但是每个目的地有且只能被参观一次(参观顺序为n的排列)。
lahub把所有可能的“旅行”都写在一张纸上,并且记下每个“旅行”所要走的路程。他对所有“旅行”的路程之和的平均值感兴趣。但是他觉得计算太枯燥了,所以就向你寻求帮助。
【输入格式】
第一行一个正整数n。
第二行n个非负整数a1,a2,....,an(1≤ai≤10^7)。
【输出格式】
两个整数,答案用最简分数形式输出,第一个为分子,第二个为分母。
【输入样例】
3
2 3 5
【输出样例】
22 3
【样例提示】
样例有6种可能的旅行:
[2, 3, 5]: 该“旅行”的路程:|2 – 0| + |3 – 2| + |5 – 3| = 5;
[2, 5, 3]: |2 – 0| + |5 – 2| + |3 – 5| = 7;
[3, 2, 5]: |3 – 0| + |2 – 3| + |5 – 2| = 7;
[3, 5, 2]: |3 – 0| + |5 – 3| + |2 – 5| = 8;
[5, 2, 3]: |5 – 0| + |2 – 5| + |3 – 2| = 9;
[5, 3, 2]: |5 – 0| + |3 – 5| + |2 – 3| = 8.
答案为 1/6 * (5+7+7+8+9+8)=44/6=22/3
【数据范围】
30% n<=10
50% n<=1000
100% n<=100000
分析:
这道题的不免会让人想起用DFS搜下去。打出来个全排列出来。为了全排列可能还用预处理两点之间的位置。不过。做这些事情。恩。还是给WA了。
而这道题再进一步思考呢?会让人想到。如果,只是对每条边进行一个处理呢?思考--->每条边(两个点之间的距离)对最终的答案的影响。那么如果我们走了这条边,我们接下来会有多少种路可以走呢,也就是接下来有多少种组合呢? 假设我们选择了Ai 与 Aj 这条路,接下来就会有(n-2)!种方案。那么Ai与Aj这条路就会走(n-2)!次。而这条路又有(n-1)种选择。因为我们可以选择在什么时候再走。这个时候方案数就又多了。是 (n-2)!*(n-1) ==(n-1)!。但是我们光枚举了两点之间的距离,没有枚举从起点开始的路径。而从头开始的路径的位置是固定的。假设我们从0到Ai。那么走完之后就有(n-1)!种方案。/-乘法原理-/。这样每次的情况又枚举完了。乘上权值就是我们最后的总和。
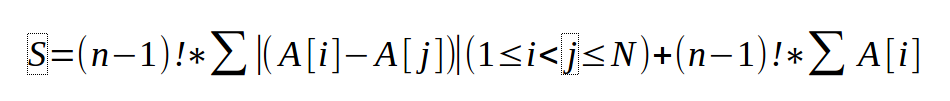
最关键的就是我们如何去枚举整个sum(abs(A[i]-A[j]);首先,我们可以确定的是。我们就只用计算从i到j 并且 (i>j)这样计算,总路程就×2就好(走过去,走回来)。
我们可以用递推来实现整个计算。我们可以发现一个规律:
假设a1 > a2 > a3 > a4,
以Ai为结尾的Ai-Aj的和为Si,
那么:
S2 = a1 - a2
S3 = a1 - a3 + a2 - a3 = (a1 - a2 + a2 - a3) + a2 - a3 = S2 + 2 *(a2 - a3)
S4 = a1 - a4 + a2 - a4 + a3 - a4 = (a1 - a3 + a3 - a4) + (a2 - a3 + a3 - a4) + (a3 - a4)
= S3 + 3 * (a3 - a4)
我们发现这里的S是可以递推的。
最后在计算结果的时候 分子是总和。而分母是总方案数n! 分数相约之后。分母就只剩一个n。那么我们就只需要计算gcd再同时除以gcd。
放出代码:
#include<cstdio>
#include<algorithm>
using namespace std;
int line[1000001];
int n;
long long int gcd(long long int a,long long int b)
{
return a%b==0 ? b : gcd(b,a%b);
}
int cmp(int a,int b)
{
return a>b;
}
int main()
{
freopen("tourist.in","r",stdin);
freopen("tourist.out","w",stdout);
long long int sum=0;
scanf("%d",&n);
for(int i=1;i<=n;++i)
{
scanf("%d",&line[i]);
sum+=line[i];
}
sort(line+1,line+1+n,cmp);
long long int k=0,ans=0;
for(int i=2;i<=n;++i)
{
k=k+(i-1)*(line[i-1]-line[i]);
ans+=k;
}
sum+=ans*2;
long long int c=gcd(sum,n);
printf("%I64d %I64d",sum/c,n/c);
fclose(stdin);
fclose(stdout);
return 0;
}