如果本文帮到了你,帮忙点个赞;
如果本文帮到了你,帮忙点个赞;
如果本文帮到了你,帮忙点个赞;
HPF 一阶RC高通滤波器详解(仿真+matlab+C语言实现)
LPF 一阶RC低通滤波器详解(仿真+matlab+C语言实现)
1 预备知识
低通滤波器(LPF)可以滤除频率高于截止频率的信号,类似的还有高通滤波器,带通滤波器,带阻滤波器。一阶RC低通滤波器的电路如下图所示;

参考了Wiki了,然后推导了一遍;首先输入输出的关系如下;
所以电容的的充电时间为 因此满足以下条件;
所以由①,②可得:
将方程进行离散化,如果输入和输出输入按照 的时间采样,那么可以将输入和输出序列化,则
序列化为:
序列化为:
因此可以将③式转化为:
因此最终滤波输出的序列 如下所示;

同样进行简化之后可以得到;
后面可以根据这个公式进行程序设计;
另外,截止频率满足;
2 simulink 仿真
这里直接根据公式③构建一搞Subsystem;
Subsystem
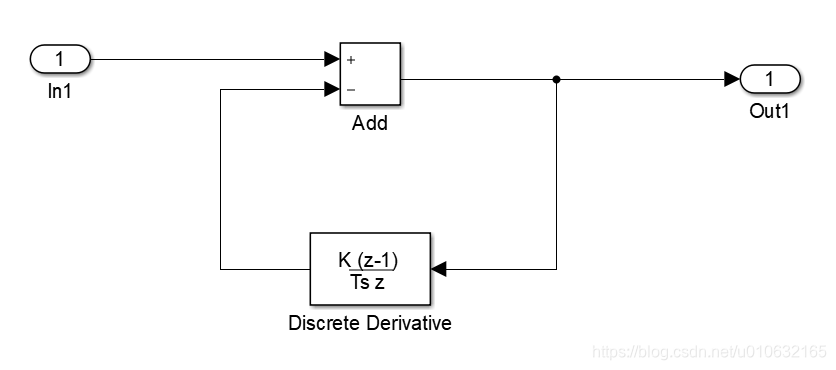
整体的仿真图如下:
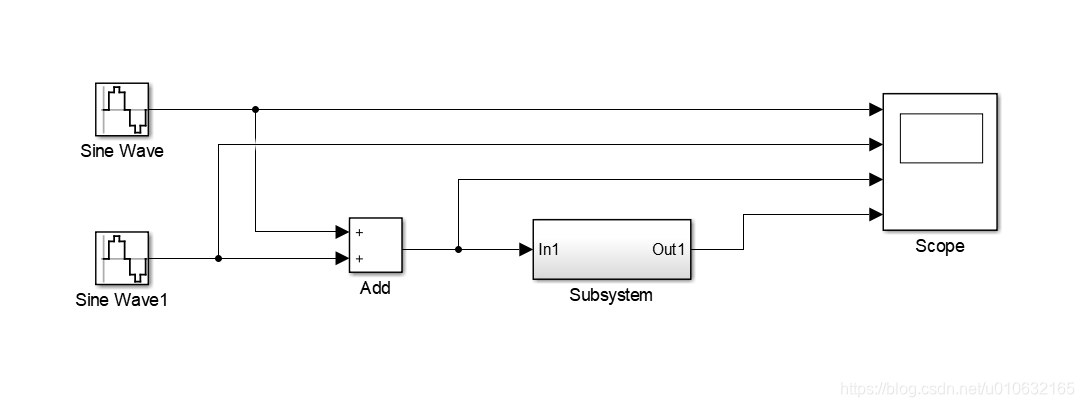
其中Sine Wave频率设置为2*pi*50

其中Sine Wave1频率设置为2*pi

所以这里需要使得2*pi*50的信号衰减,所以根据,截止频率的计算公式,可以改变增益的值,具体如下所示;

3 simulink 运行结果
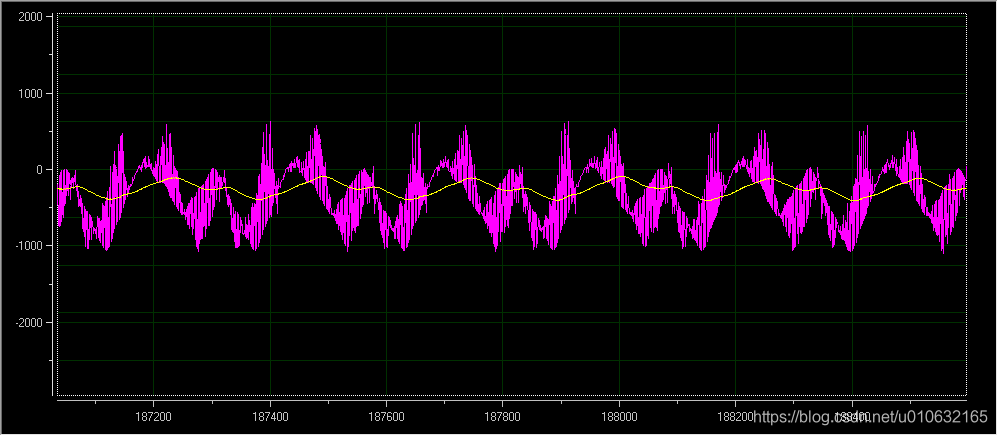
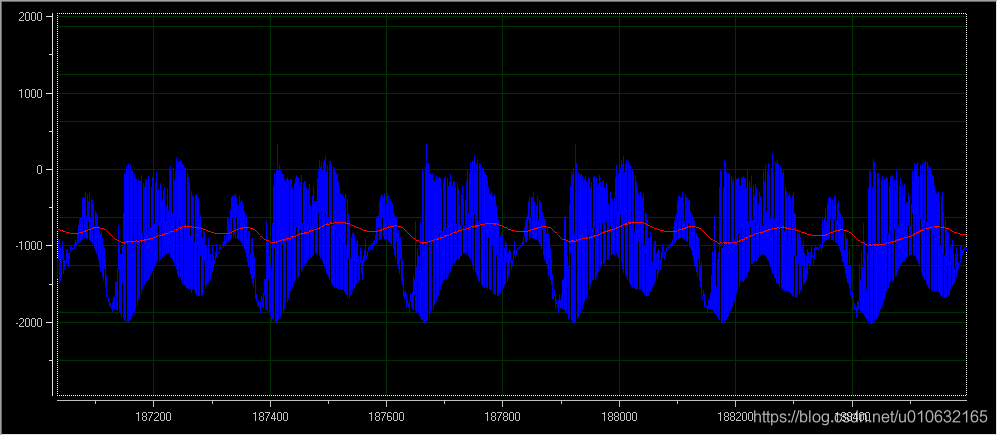
最终的仿真的运行结果如下图所示;
Gain Value为0.005
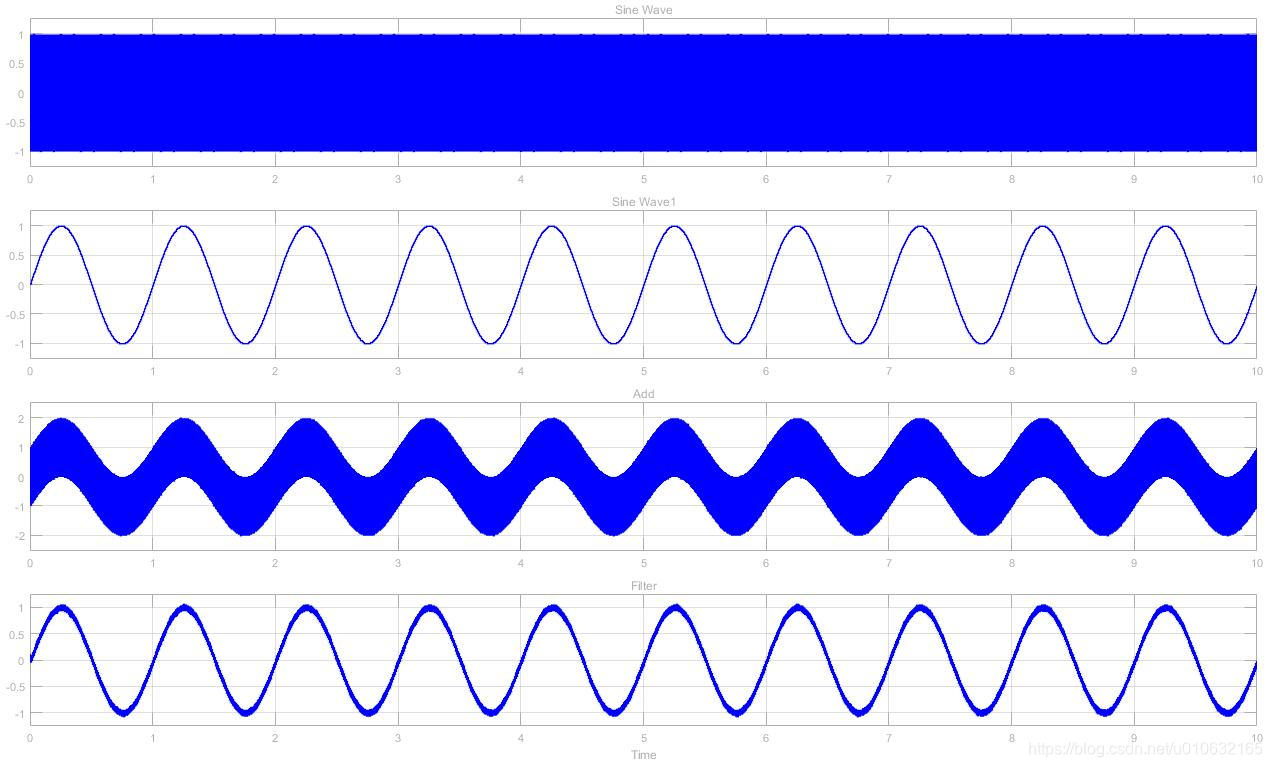
Gain Value为0.0318
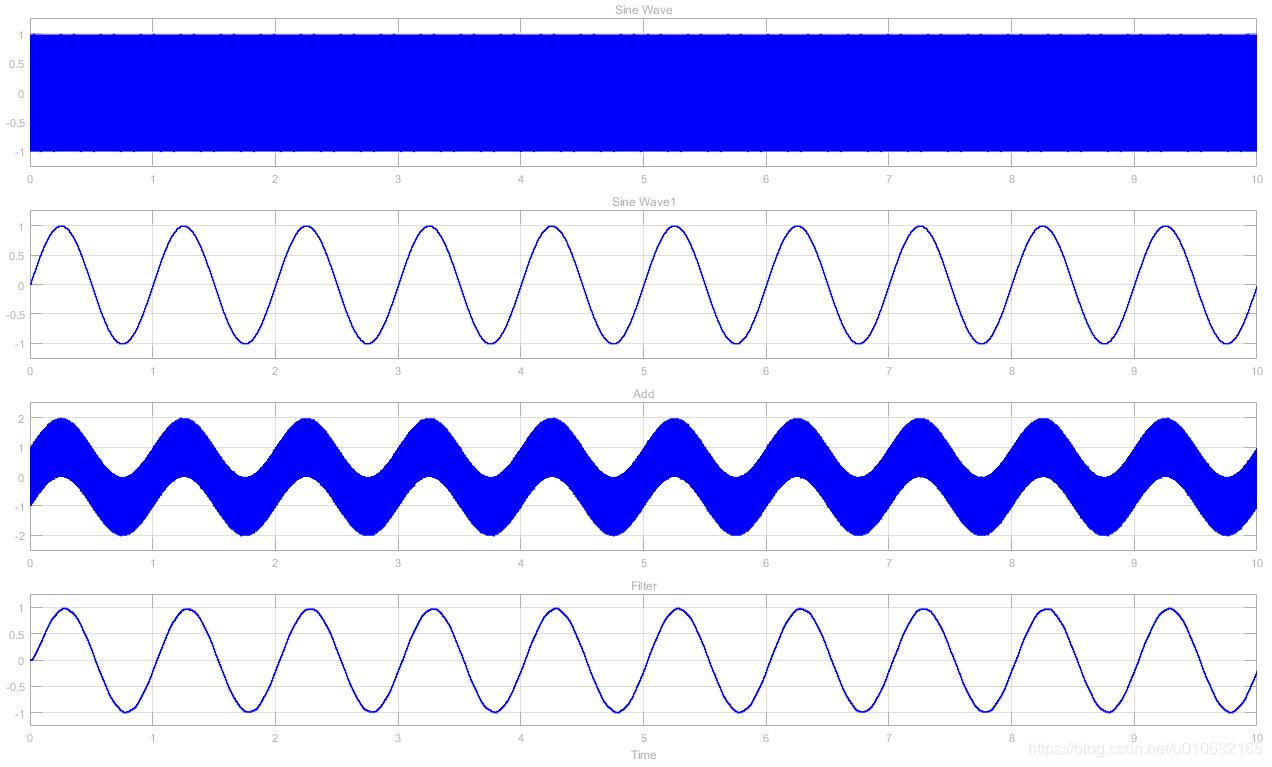
4 matlab实现
根据公式
实现数字一阶RC低通滤波器,具体matlab程序如下;
Serial = 0:0.1:100;
Fs = 1;
Phase = 0;
Amp = 1;
% 高频信号
N0 = 2*pi*Fs*Serial - Phase;
X0 = Amp*sin(N);
subplot(4,1,1);
plot(X0);
% 低频信号
Fs = 0.02;
N1 = 2*pi*Fs*Serial - Phase;
X1 = Amp*sin(N1);
subplot(4,1,2);
plot(X1);
% 高频低频叠加的信号
X2=X0+X1;
subplot(4,1,3);
plot(X2);
%Xi-Yi=RC*(Yi - Yi-1)/DetalT
len = length(X2);
X3=X2;
p=0.05;
% 一阶RC滤波得到X3
for i=2:len
X3(i) = p*X2(i)+(1-p)*X3(i-1);
end
subplot(4,1,4);
plot(X3);
5 matlab运行结果
运行结果如下所示;
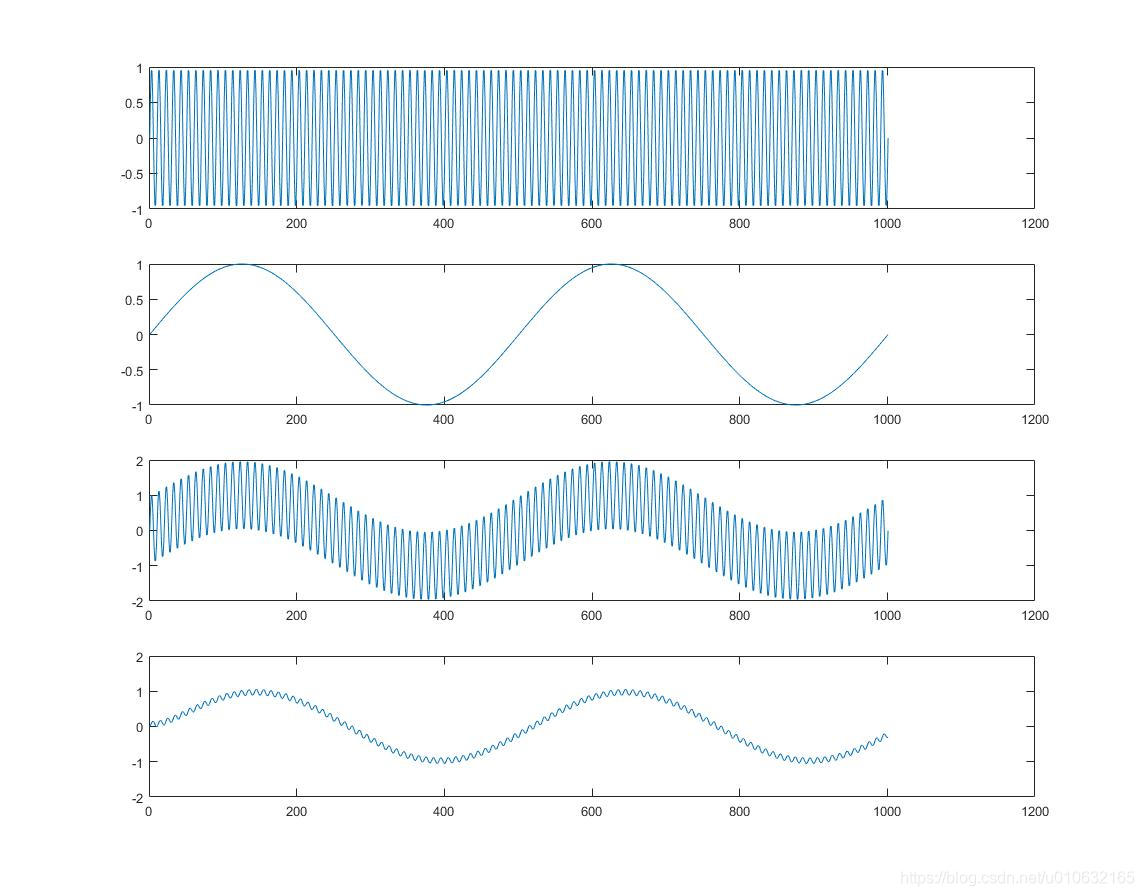
6 C语言实现
low_filter.h
typedef struct
{
int16_t Input;
int16_t Output[2];
int32_t FilterTf;
int32_t FilterTs;
int32_t Kr;
int32_t Ky;
} low_filter;
void low_filter_init(low_filter *v);
int16_t low_filter_calc(low_filter *v);
其中;
FilterTs为采样时间;FilterTf为RC时间常数
具体参考下图;

low_filter.c
void low_filter_init(low_filter *v){
v->Kr = v->FilterTs*1024/(v->FilterTs + v->FilterTf);
v->Ky = v->FilterTf*1024/(v->FilterTs + v->FilterTf);
}
int16_t low_filter_calc(low_filter *v){
int32_t tmp = 0;
tmp = ((int32_t)v->Kr*v->Input + v->Ky*v->Output[1])/1024;
if(tmp>32767){
tmp = 32767;
}
if( tmp < -32768){
tmp = -32768;
}
v->Output[0] = (int16_t)tmp;
v->Output[1] = v->Output[0];
return v->Output[0];
}
7 C语言运行结果
实际测试结果