概念
A tree is a nonlinear data structure, compared to arrays, linked lists, stacks and queues which are linear data structures. A tree can be empty with no nodes or a tree is a structure consisting of one node called the root and zero or one or more subtrees.
树是一个非线性的数据结构,相比较而言,数组,链表,栈和队列等等就是线性的数据结构。树可以为空,不包含任何节点,或者树可以称为由一个根节点和零个或者多个子树构成的。
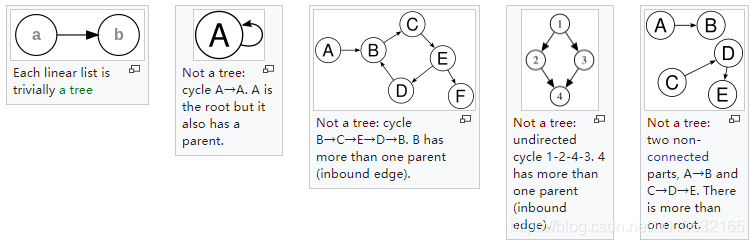
判断是否是一颗树的条件:
- 有且只有一个根节点;
- 有若干个互不相交的子树;
- 根节点(root)没有父节点;
- 一个节点有且只有一个父节点(根节点除外);
- 节点可以有多个子节点;
和树相关的一些术语,查阅了网上的一些资料,做了一下整理;
| Terminology(术语) | Explaining(解释) |
|---|---|
| Root(根) | 树中的顶级节点 |
| Child(子节点) | Root的每一个子树的根叫做Root的子节点(Child) |
| Parent(父节点) | Root是每一个子树的根的父节点(Parent) |
| Siblings(兄弟节点) | 一些具有相同父节点的节点称为兄弟节点 |
| Descendant(后代) | 对任意节点x,从根节点到节点x的所有节点都是x的祖先 |
| Ancestor(祖先) | 对任意节点x,从节点x到叶子节点的所有节点都是x的后代 |
| Leaf(叶子节点) | 没有子节点的节点 |
| Degree(度) | 子节点的个数(最大子节点的度称为树的度) |
| Edge(边) | 父节点和子节点相连的一个路径 |
| Depth(深度) | 节点的深度定义为:当前节点和根之间的边数。 |
| Height of node(节点的高) | 节点的高度是该节点与后代节点之间最长路径上的边数,所以叶子节点高度为0 |
| Height of tree(树的高) | 树的高度是其根节点的高度 |
| Forest (森林) | 多颗互不相交的树组成的集合 |
树的分类
按照个人的理解进行分类;
- 一般树:任意一个节点的子节点的个数都不受限制;
- 二叉树:任意一个节点的子节点的个数最多只有两个;
- 一般二叉树
- 满二叉树:在不增加树的层数的前提下,无法再多添加一个节点的二叉树
- 完全二叉树:如果只是删除了满二叉树的最底层最右边的连续若干个节点,则这样形成的二叉树叫完全二叉树;
- 森林:n个互不相交的树的集合;
树的数据结构
typedef struct TreeNode *PtreNode; //前向声明
struct TreeNode {
ElementType element;
PtreNode FirstChild;
PtreNode NextSibling;
}
总结
大部分的知识点主要参考了wiki上的解释,这里对于二叉树的分类都是点到即止,其实需要自己结合实践写代码实现一下,深入了解知识点和应用场景,以加深理解,如有错误的地方,希望指正。