【题解】（LGJ原创）蝴蝶旅客

题目描述

歌姬什么的，不干了啦！星尘要旅游！

于是星尘换上了蝴蝶套装在一片为 (p) 层每层n行m列的矩阵中开始了她的旅行，她从 ((1,1,1)) 出发，到 ((x,y,z)) 去。这片空间里有一些是不能通过的，因为这些空间内没有以太之尘，星尘飞不起来。现在告诉你哪里有以太之尘，请你依照 (x) 轴正 (（x+1）) 、(y) 轴正 (（y+1）)、(z) 轴正 (（z+1）)、(x) 轴负 (（x-1）)、(y) 轴负 (（y-1）)、(z) 轴负 (（z-1）)的顺序找到到达终点的所有路径，

对于每一条路径，不能走回头路，因为走过的路也没有以太之尘。记住，每条路径之间不会互相干扰，这一条走过某个位置不影响另一条路径走过这个位置。如果不能到达输出 (-1)。

输入格式

第一行六个整数表示 (p) 层每层 (n) 行 (m) 列和终点坐标 (x、y、z)
接下来有 (p) 个矩阵，每个矩阵有 (n) 行 (m) 列，(1) 表示可以通过。

输出格式

输出从起点到终点的所有路径，不存在输出 (-1)

样例输入

3 3 3 3 3 1

1 1 1
0 0 1
0 0 1

1 0 0
0 0 0
0 0 1

1 1 1
0 0 1
0 0 1

样例输出

(1,1,1)->(1,2,1)->(1,3,1)->(2,3,1)->(3,3,1)
(1,1,1)->(1,1,2)->(1,1,3)->(1,2,3)->(1,3,3)->(2,3,3)->(3,3,3)->(3,3,2)->(3,3,1)

数据范围

(n,m,ple 10)

题目大意

LGJ出的毒瘤搜索……但是这个……三维搜索……有（yi）点复杂啊……

分析

如果要输出路径的话就必须用深搜勒~ 但是，“在写这道题被 (TLE) 狂虐中我明白了，越是优化剪枝（其实并没有什么可剪的）抓耳挠腮，越会发现 (dfs) 的力量是有限的，除非超越 (dfs)。……所以……我用 (bfs) 辣！JOJO！[哔——]”

注意到如果根本无法到达终点的话，(dfs) 就会像无头苍蝇一样到处搜索，时间复杂度大大提高，所以，可以考虑先用 (bfs) 搜索一遍判断是否可以到达终点，如果不能直接输出 (-1) 结束程序，这样便使得 (dfs) 不会因为无法到达终点而时间超限。

确定算法之后就来到了这道题最另人头秃的地方了：确定 (x、y、z) 轴。
将样例画出来之后如下图所示：
（黑色、蓝色、红色分别为不同的层）

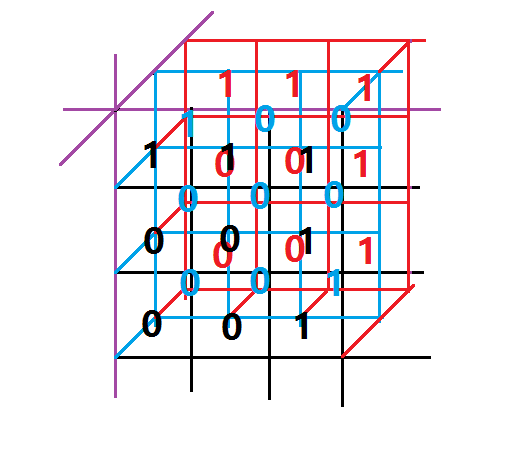
题目中的两条路径分别为：

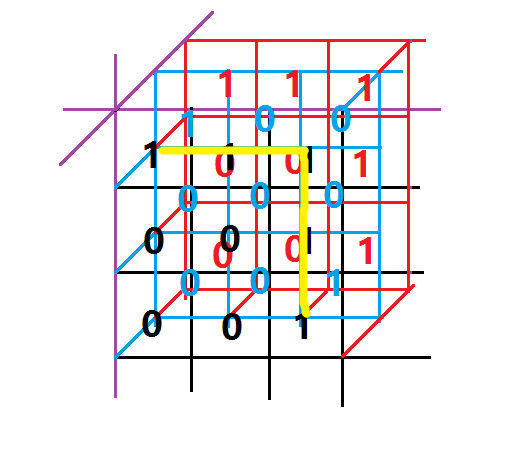
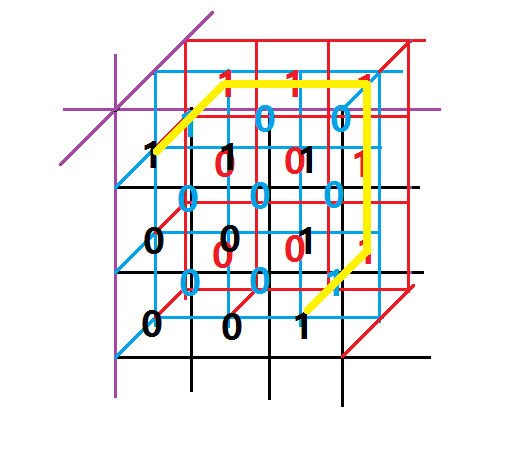
所以，题目中的坐标 ((x,y,z)) 指的是第 (x) 层 (y) 行 (z) 列的点，在搜索或输入时一定要注意！

Code

#include <bits/stdc++.h>
using namespace std;
int a[11][11][11],v[11][11][11];
struct node{
    int x,y,z;
}d[1010];//bfs的队列 
int dx[6]={1,0,0,-1,0,0},dy[6]={0,1,0,0,-1,0},dz[6]={0,0,1,0,0,-1};//坐标移动数组 
int px[1010],py[1010],pz[1010];//输出(put_out)数组 
int m,n,p,zx,zy,zz;
bool bfs()//判断是否能够到达终点 
{
    int head=1,tail=2;
    while(head<=tail){
        if(d[head].x==zx&&d[head].y==zy&&d[head].z==zz)
            return true;
        for(int i=0;i<=5;i++){
            int tx=d[head].x+dx[i],ty=d[head].y+dy[i],tz=d[head].z+dz[i];
            if(!v[tz][tx][ty]&&a[tz][tx][ty]){//【注意】在这里我的坐标是(z,x,y)！ 
                v[tz][tx][ty]=1;//第z层的第x行第y列的点 
                d[tail].x=tx;
                d[tail].y=ty;
                d[tail].z=tz;
                tail++;
            }
        }
        head++;
    }
    return false;
}
void put_out(int x)
{
    for(int i=0;i<x;i++)
        printf("(%d,%d,%d)->",px[i],py[i],pz[i]);
    printf("(%d,%d,%d)
",px[x],py[x],pz[x]);
    return;
}
void dfs(int x,int y,int z,int cnt)
{
    if(x<1||y<1||z<1||x>n||y>m||z>p) return;//这里x、y、z对应的n、m、p和输入时的顺序有所不同
    if(x==zx&&y==zy&&z==zz){//x指层数，y、z才是横纵坐标哦
        put_out(cnt);
        return;
    }
    for(int i=0;i<6;i++){
        int tx=x+dx[i],ty=y+dy[i],tz=z+dz[i];
        if(a[tz][tx][ty]){
            a[tz][tx][ty]=0;
            cnt++;
            px[cnt]=tx;
            py[cnt]=ty;
            pz[cnt]=tz;
            dfs(tx,ty,tz,cnt);
            cnt--;
            a[tz][tx][ty]=1;
        }
    }
}
int main()
{
    scanf("%d%d%d%d%d%d",&p,&n,&m,&zx,&zy,&zz);
    for(int i=1;i<=p;i++)//【注意！】a(i,j,k)在这里记录的是第i层j行k列的点 
        for(int j=1;j<=n;j++)//如果在这里的输入改为a[j][k][i]，上面的搜索中就可以用x,y,z了 
            for(int k=1;k<=m;k++)
                scanf("%d",&a[i][j][k]);
    d[1].x=d[1].y=d[1].z=1;
    memset(v,0,sizeof(0));
    v[1][1][1]=0;
    if(!bfs()){//如果不能到达直接输出-1 
        printf("-1");
        return 0;
    }
    px[0]=py[0]=pz[0]=1;
    a[1][1][1]=0;
    dfs(1,1,1,0);
    return 0;
}

说实话是一道很好的搜索题目，同时考察了 (dfs) 和 (bfs)。

LGJ NB!!!（破音）

最后，完结撒fa~