2017/3/1
215. Kth Largest Element in an Array

Find the kth largest element in an unsorted array. Note that it is the kth largest element in the sorted order, not the kth distinct element. For example, Given [3,2,1,5,6,4] and k = 2, return 5. Note: You may assume k is always valid, 1 ≤ k ≤ array's length.
自己的代码:

/** * 先利用Arrays的sort()函数对给定的数组进行排序, * 得到的数组是升序排列的,然后获得数组的长度,重新申请一个新的数组, * 将之前的数组从最后一个开始,一次存入新数组的第一个位置开始, * 这样新的数组就成了降序排列,这是返回数组当中的第k个位置的数值即可 * @param nums * @param k * @return */ public class Solution { public int findKthLargest(int[] nums, int k) { Arrays.sort(nums); int n=nums.length; int[] res=new int[n]; for(int i=nums.length-1,j=0;i>=0;i--,j++) { res[j]=nums[i]; } return res[k-1]; } }
另一种解法是利用PriorityQueue,关于priorityQueue的使用详情,博客如下http://www.cnblogs.com/CarpenterLee/p/5488070.html,具体代码如下:

class Solution { /** * @return */ public int findKthLargest(int[] nums, int k) { PriorityQueue<Integer> largek = new PriorityQueue<Integer>(); for (int i : nums) { largek.add(i); if (largek.size() > k) { largek.poll(); } } return largek.poll(); } };
最优解:O(N lg N) running time + O(1) memory

public int findKthLargest(int[] nums, int k) { final int N = nums.length; Arrays.sort(nums); return nums[N - k]; }
---------------------------------------------------------------------------------------------------------------------------------
2017/3/2
150. Evaluate Reverse Polish Notation

Evaluate the value of an arithmetic expression in Reverse Polish Notation. Valid operators are +, -, *, /. Each operand may be an integer or another expression. Some examples: ["2", "1", "+", "3", "*"] -> ((2 + 1) * 3) -> 9 ["4", "13", "5", "/", "+"] -> (4 + (13 / 5)) -> 6
关于Stack的具体介绍见博客:http://www.cnblogs.com/skywang12345/p/3308852.html
自己的代码:

public class Solution { /** * Author: wanghaibo * Complexity Time: O(n); Space: O(n) * Explaination: 利用Stack实现,首先遍历tokens数组, * 如果字符串不是操作符是数字,则进栈,如果是操作符,则将两个 * 数字出栈,根据操作符得到结果后重新压入栈 * @param tokens * @return */ public int evalRPN(String[] tokens) { if (tokens.length == 1) { return Integer.parseInt(tokens[0]); } Stack<String> stack = new Stack<String>(); for (String i : tokens) { if (isoperator(i) != 0) { int a = Integer.parseInt(stack.pop()); int b = Integer.parseInt(stack.pop()); String c = ""; if (i.equals("+")) { c = String.valueOf(b + a); } else if (i.equals("-")) { c = String.valueOf(b - a); } else if (i.equals("*")) { c = String.valueOf(a * b); } else if (i.equals("/")) { c = String.valueOf(b / a); } stack.push(c); } else { stack.push(i); } } return Integer.parseInt(stack.pop()); } public int isoperator(String s) { if (s.equals("+")) { return 1; } else if (s.equals("-")) { return 2; } else if (s.equals("*")) { return 3; } else if (s.equals("/")) { return 4; }else { return 0; } } }
最优解:

import java.util.Stack; public class Solution { public int evalRPN(String[] tokens) { int a,b; Stack<Integer> S = new Stack<Integer>(); for (String s : tokens) { if(s.equals("+")) { S.add(S.pop()+S.pop()); } else if(s.equals("/")) { b = S.pop(); a = S.pop(); S.add(a / b); } else if(s.equals("*")) { S.add(S.pop() * S.pop()); } else if(s.equals("-")) { b = S.pop(); a = S.pop(); S.add(a - b); } else { S.add(Integer.parseInt(s)); } } return S.pop(); } }
----------------------------------------------------------------------------------------------------------------------------------------
2017/3/5
373. Find K Pairs with Smallest Sums

You are given two integer arrays nums1 and nums2 sorted in ascending order and an integer k. Define a pair (u,v) which consists of one element from the first array and one element from the second array. Find the k pairs (u1,v1),(u2,v2) ...(uk,vk) with the smallest sums. Example 1: Given nums1 = [1,7,11], nums2 = [2,4,6], k = 3 Return: [1,2],[1,4],[1,6] The first 3 pairs are returned from the sequence: [1,2],[1,4],[1,6],[7,2],[7,4],[11,2],[7,6],[11,4],[11,6] Example 2: Given nums1 = [1,1,2], nums2 = [1,2,3], k = 2 Return: [1,1],[1,1] The first 2 pairs are returned from the sequence: [1,1],[1,1],[1,2],[2,1],[1,2],[2,2],[1,3],[1,3],[2,3] Example 3: Given nums1 = [1,2], nums2 = [3], k = 3 Return: [1,3],[2,3] All possible pairs are returned from the sequence: [1,3],[2,3]
先声明一个优先队列,重写compare()函数,实现大顶堆,然后依次入堆,构造一个大顶堆。然后声明一个LinkedListed,将大顶堆根插入双向链表中,注意k,只需要插入k个就行,如果小于k个,直接返回,代码如下:

public List<int[]> kSmallestPairs(int[] nums1, int[] nums2, int k) { List<int[]> res = new LinkedList<>(); Queue<int[]> queue = new PriorityQueue<>(k,new Comparator<int[]>(){ public int compare(int[] o1,int[] o2){ int tmp1 = o1[0]+o1[1]; int tmp2 = o2[0]+o2[1]; return tmp1 - tmp2; } }); for(int i = 0;i<nums1.length;i++){ for(int j = 0;j<nums2.length;j++){ queue.add(new int[]{nums1[i],nums2[j]}); } } while(k-->0){ int[] tmp = queue.poll(); if(tmp == null) break; res.add(tmp); } return res; }
需要了解LinkedList,具体链接http://www.cnblogs.com/chenssy/p/3514524.html,做不出来主要是因为不了解LinekedList和PriorityQueue,需要多看!!!
最优解:

Basic idea: Use min_heap to keep track on next minimum pair sum, and we only need to maintain K possible candidates in the data structure. Some observations: For every numbers in nums1, its best partner(yields min sum) always strats from nums2[0] since arrays are all sorted; And for a specific number in nums1, its next candidate sould be [this specific number] + nums2[current_associated_index + 1], unless out of boundary;) Here is a simple example demonstrate how this algorithm works. image The run time complexity is O(kLogk) since que.size <= k and we do at most k loop. public class Solution { public List<int[]> kSmallestPairs(int[] nums1, int[] nums2, int k) { PriorityQueue<int[]> que = new PriorityQueue<>((a,b)->a[0]+a[1]-b[0]-b[1]); List<int[]> res = new ArrayList<>(); if(nums1.length==0 || nums2.length==0 || k==0) return res; for(int i=0; i<nums1.length && i<k; i++) que.offer(new int[]{nums1[i], nums2[0], 0}); while(k-- > 0 && !que.isEmpty()){ int[] cur = que.poll(); res.add(new int[]{cur[0], cur[1]}); if(cur[2] == nums2.length-1) continue; que.offer(new int[]{cur[0],nums2[cur[2]+1], cur[2]+1}); } return res; } }
------------------------------------------------------------------------------------------------------------------------------------------------
2017/3/6
202. Happy Number

Write an algorithm to determine if a number is "happy". A happy number is a number defined by the following process: Starting with any positive integer, replace the number by the sum of the squares of its digits, and repeat the process until the number equals 1 (where it will stay), or it loops endlessly in a cycle which does not include 1. Those numbers for which this process ends in 1 are happy numbers. Example: 19 is a happy number 12 + 92 = 82 82 + 22 = 68 62 + 82 = 100 12 + 02 + 02 = 1
代码如下:

/** * 或得一个数每一位的平方相加之和 * @param n * @return */ public int squaresum(int n) { int sum = 0, tmp; while (n != 0) { tmp = n % 10; sum +=tmp * tmp; n /= 10; } return sum; } /** * 将中间结果存入HashSet,如果发现结果为1,则返回true,如果结果中出现了n,则代表 * 出现环,返回false,否则就将中间结果存入set中 * @param n * @return */ public boolean isHappy(int n) { if (n <= 0) return false; Set<Integer> set = new HashSet<Integer>(); set.add(n); while(true) { n = squaresum(n); if (n == 1) return true; else if (set.contains(n)) return false; else set.add(n); } }
另一种解法是用快慢指针,代码如下:

/** * 或得一个数每一位的平方相加之和 * @param n * @return */ public int squaresum(int n) { int sum = 0, tmp; while (n != 0) { tmp = n % 10; sum +=tmp * tmp; n /= 10; } return sum; } /** * 新建一个快指针和一个慢指针 * 慢指针只求一次,下一个数;块指针每次求两次,下一个数 * 如果快指针的值和慢指针的值相等,则返回false * 快指针的值等于1,则返回true * @param n * @return */ public boolean isHappy(int n) { int slow = n; int fast = n; while(true) { slow = squaresum(slow); fast = squaresum(squaresum(fast)); if (fast == 1) return true; if (slow == fast) return false; } }
---------------------------------------------------------------------------------------------------------------------------------------
2017/3/7
263. Ugly Number

Write a program to check whether a given number is an ugly number. Ugly numbers are positive numbers whose prime factors only include 2, 3, 5. For example, 6, 8 are ugly while 14 is not ugly since it includes another prime factor 7. Note that 1 is typically treated as an ugly number.
代码如下:

/** * 首先判断输入的数据是否小于等于0,如果是,则肯定不是ugly数,返回false * 判断是不是1,是的话肯定是ugly数 * 否则 * 如果能对2,3,5进行整除,则用num除以2,3,5,只要num>1时,循环进行 * 否则返回false * @param num * @return */ public boolean isUgly(int num) { if (num <= 0) { return false; } if (num == 1) { return true; } while (num > 1) { if (num % 2 == 0) { num /= 2; } else if (num % 3 == 0) { num /= 3; } else if (num % 5 == 0) { num /= 5; } else { return false; } } return true; }
最优解与以上类似,代码如下:

public boolean isUgly(int num) { if (num <= 0) {return false;} if (num == 1) {return true;} if (num % 2 == 0) { return isUgly(num/2); } if (num % 3 == 0) { return isUgly(num/3); } if (num % 5 == 0) { return isUgly(num/5); } return false; }
-------------------------------------------------------------------------------------------------------------------------------------------------
2017/3/8
264. Ugly Number II

Write a program to find the n-th ugly number. Ugly numbers are positive numbers whose prime factors only include 2, 3, 5. For example, 1, 2, 3, 4, 5, 6, 8, 9, 10, 12 is the sequence of the first 10 ugly numbers. Note that 1 is typically treated as an ugly number, and n does not exceed 1690.
代码如下:

public class Solution { /** * 首先将1加入到集合当中,设置三个指针,分别取出三个指针对应的list * 中的值,分别向相关的数,挑选最小的一个数作为下一个Ugly数,加入 * list中,只有最小的数对应的那个指针才进行+1操作 * 最后返回第n个数 * @param n * @return */ public int nthUglyNumber(int n) { ArrayList<Integer> list = new ArrayList<Integer>(); list.add(1); int p2 = 0; int p3 = 0; int p5 = 0; while (list.size() < n) { int ugly2 = list.get(p2) * 2; int ugly3 = list.get(p3) * 3; int ugly5 = list.get(p5) * 5; int min = Math.min(ugly2, Math.min(ugly3, ugly5)); list.add(min); if (min == ugly2) p2++; if (min == ugly3) p3++; if (min == ugly5) p5++; } return list.get(n-1); } }
最优解和解析如下:

The idea of this solution is from this page:http://www.geeksforgeeks.org/ugly-numbers/ The ugly-number sequence is 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, … because every number can only be divided by 2, 3, 5, one way to look at the sequence is to split the sequence to three groups as below: (1) 1×2, 2×2, 3×2, 4×2, 5×2, … (2) 1×3, 2×3, 3×3, 4×3, 5×3, … (3) 1×5, 2×5, 3×5, 4×5, 5×5, … We can find that every subsequence is the ugly-sequence itself (1, 2, 3, 4, 5, …) multiply 2, 3, 5. Then we use similar merge method as merge sort, to get every ugly number from the three subsequence. Every step we choose the smallest one, and move one step after,including nums with same value. Thanks for this author about this brilliant idea. Here is my java solution public class Solution { public int nthUglyNumber(int n) { int[] ugly = new int[n]; ugly[0] = 1; int index2 = 0, index3 = 0, index5 = 0; int factor2 = 2, factor3 = 3, factor5 = 5; for(int i=1;i<n;i++){ int min = Math.min(Math.min(factor2,factor3),factor5); ugly[i] = min; if(factor2 == min) factor2 = 2*ugly[++index2]; if(factor3 == min) factor3 = 3*ugly[++index3]; if(factor5 == min) factor5 = 5*ugly[++index5]; } return ugly[n-1]; } }
----------------------------------------------------------------------------------------------------------------------------------------------
2017/3/14
278. First Bad Version

You are a product manager and currently leading a team to develop a new product. Unfortunately, the latest version of your product fails the quality check. Since each version is developed based on the previous version, all the versions after a bad version are also bad. Suppose you have n versions [1, 2, ..., n] and you want to find out the first bad one, which causes all the following ones to be bad. You are given an API bool isBadVersion(version) which will return whether version is bad. Implement a function to find the first bad version. You should minimize the number of calls to the API.
利用二分查找,最优代码如下:

public class Solution extends VersionControl { public int firstBadVersion(int n) { int lo = 1, hi = n; while (lo <= hi) { int mid = lo + (hi - lo) / 2; if (isBadVersion(mid)) { hi = mid - 1; } else { lo = mid + 1; } } return lo; } }
-----------------------------------------------------------------------------------------------------------------------------------------------
2017/3/16
74. Search a 2D Matrix

Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties: Integers in each row are sorted from left to right. The first integer of each row is greater than the last integer of the previous row. For example, Consider the following matrix: [ [1, 3, 5, 7], [10, 11, 16, 20], [23, 30, 34, 50] ] Given target = 3, return true.
解法一如下:

/** * 遍历每一行,对每一行进行二分查找,假设有m行n列,则算法的时间复杂度为mlog(n) * @param matrix * @param target * @return */ public boolean searchMatrix(int[][] matrix, int target) { boolean flag = false; if (matrix.length == 0 || matrix == null || matrix[0] == null || matrix[0].length ==0) { return false; } for (int i = 0; i < matrix.length; i++) { int lo = 0; int n = matrix[i].length; int hi = n - 1; while (lo <= hi) { int mid = lo + (hi - lo) / 2; if (matrix[i][mid] == target) { flag = true; break; } if (matrix[i][mid] > target) { hi = mid - 1; } if (matrix[i][mid] < target) { lo = mid + 1; } } } return flag; }
解法二如下:

/** * 从左下角开始查找,如果target小于这个数,则行数减一,如果大于这个数,则列数加一 * 时间复杂度为O(m)+O(n),m为行数,n为列数 * @param matrix * @param target * @return */ public boolean searchMatrix(int[][] matrix, int target) { boolean flag = false; if (matrix.length == 0 || matrix == null || matrix[0] == null || matrix[0].length == 0) { return false; } int m = matrix.length; int n = matrix[0].length; int i = m - 1; int j = 0; while (i >= 0 && j < n) { if (matrix[i][j] < target) { j++; } else if (matrix[i][j] > target) { i--; } else { flag = true; break; } } return flag; }
解法三如下:

/** * 由于数组是有序递增的,那么可以把二维数组转换为一位数组进行操作 * 假设二维数组每一行有n列,那么一位数组中下标为x的数对应的二维数组中 * 的数的为matrix[x/n][x%n],利用二分法对一维数组进行查找即可 * 时间复杂度为O(log(m*n)) * @param matrix * @param target * @return */ public boolean searchMatrix(int[][] matrix, int target) { boolean flag = false; if (matrix.length == 0 || matrix == null || matrix[0] == null || matrix[0].length == 0) { return false; } int m = matrix.length; int n = matrix[0].length; int left = 0; int right = m * n - 1; while (left <= right) { int mid = left + (right - left) / 2; int num = matrix[mid / n][mid % n]; if (num == target) { flag = true; break; } else if (num > target) { right = mid - 1; } else if (num < target) { left = mid + 1; } } return flag; }
解法四还可以将target的值于每一行的第一个元素进行比较,找到第一个不大于target的数,并获得这一行,在这一行进行二分查找,这种解法的时间复杂度是O(logm)+O(logn),算是时间复杂度最好的解法。具体的代码如下:

public class Solution { public boolean searchMatrix(int[][] matrix, int target) { if (matrix == null || matrix.length == 0 || matrix[0] == null || matrix[0].length == 0) { return false; } int low = 0; int high = matrix.length - 1; int mid = 0; while (low + 1 < high) { mid = low + ((high - low) >> 1); if (matrix[mid][0] == target) { return true; } else if (matrix[mid][0] > target) { high = mid; } else { low = mid; } } int index = matrix[high][0] <= target ? high : low; low = 0; high = matrix[0].length - 1; while (low + 1 < high) { mid = low + ((high - low) >> 1); if (matrix[index][mid] == target) { return true; } else if (matrix[index][mid] > target) { high = mid; } else { low = mid; } } if (matrix[index][low] == target || matrix[index][high] == target) { return true; } return false; } }
-------------------------------------------------
240. Search a 2D Matrix II

Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties: Integers in each row are sorted in ascending from left to right. Integers in each column are sorted in ascending from top to bottom. For example, Consider the following matrix: [ [1, 4, 7, 11, 15], [2, 5, 8, 12, 19], [3, 6, 9, 16, 22], [10, 13, 14, 17, 24], [18, 21, 23, 26, 30] ] Given target = 5, return true. Given target = 20, return false.
和上一题差不多,解法一如下

/** * 遍历每一行,对每一行进行二分查找,假设有m行n列,则算法的时间复杂度为mlog(n) * @param matrix * @param target * @return */ public boolean searchMatrix(int[][] matrix, int target) { boolean flag = false; if (matrix.length == 0 || matrix == null || matrix[0] == null || matrix[0].length ==0) { return false; } for (int i = 0; i < matrix.length; i++) { int lo = 0; int n = matrix[i].length; int hi = n - 1; while (lo <= hi) { int mid = lo + (hi - lo) / 2; if (matrix[i][mid] == target) { flag = true; break; } if (matrix[i][mid] > target) { hi = mid - 1; } if (matrix[i][mid] < target) { lo = mid + 1; } } } return flag; }
解法二如下:

/** * 从左下角开始查找,如果target小于这个数,则行数减一,如果大于这个数,则列数加一 * 时间复杂度为O(m)+O(n),m为行数,n为列数 * @param matrix * @param target * @return */ public boolean searchMatrix(int[][] matrix, int target) { boolean flag = false; if (matrix.length == 0 || matrix == null || matrix[0] == null || matrix[0].length == 0) { return false; } int m = matrix.length; int n = matrix[0].length; int i = m - 1; int j = 0; while (i >= 0 && j < n) { if (matrix[i][j] < target) { j++; } else if (matrix[i][j] > target) { i--; } else { flag = true; break; } } return flag; }
---------------------------------------------------------------------------------------------------------------------------------
2017/3/17
153. Find Minimum in Rotated Sorted Array

Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand. (i.e., 0 1 2 4 5 6 7 might become 4 5 6 7 0 1 2). Find the minimum element. You may assume no duplicate exists in the array.
两种解法,第一种:

/** * 利用position记录最小值的位置,如果从开始到结尾递增,则position肯定等于0, * 即第一个数。否则比较相邻的两个元素,如果左边的大于右边的,那么右边的肯定是最小的元素, * 记录下右边元素的位置,时间复杂度为O(n) * @param nums * @return */ public int findMin(int[] nums) { int position = 0; for (int i = 0; i < nums.length - 1; i++) { if(nums[i] > nums[i+1]) { position = i + 1; break; } } return nums[position]; }
第二种解法是利用二分查找:

public class Solution { public int findMin(int[] nums) { if (nums.length == 0 || nums == null) { return -1; } int low = 0; int high = nums.length - 1; if (nums[low] < nums[high]) { return nums[low]; } int mid; while (low < high) { mid = low + ((high - low) >> 1); if (nums[mid] > nums[high]) { low = mid + 1; } else { high = mid; } } return nums[low]; } }
154. Find Minimum in Rotated Sorted Array II

Follow up for "Find Minimum in Rotated Sorted Array": What if duplicates are allowed? Would this affect the run-time complexity? How and why? Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand. (i.e., 0 1 2 4 5 6 7 might become 4 5 6 7 0 1 2). Find the minimum element. The array may contain duplicates.
解法跟上一题类似,一定要注意,当区间是开区间low<high时,要注意nums[mid]一定是要与nums[right]比较的,最后的值下标是low,有重复值的时候,只需要high--就行了,具体代码如下:

public class Solution { public int findMin(int[] nums) { int low = 0; int high = nums.length - 1; if (nums[low] < nums[high]) { return nums[low]; } int mid; while (low < high) { mid = low + ((high - low) >> 1); if (nums[mid] > nums[high]) { low = mid + 1; } else if (nums[mid] < nums[high]) { high = mid; } else { high--; } } return nums[low]; } }
-------------------------------------------------------------------------------------------------------------------------------------
2017/3/30
406. Queue Reconstruction by Height

Suppose you have a random list of people standing in a queue. Each person is described by a pair of integers (h, k), where h is the height of the person and k is the number of people in front of this person who have a height greater than or equal to h. Write an algorithm to reconstruct the queue. Note: The number of people is less than 1,100. Example Input: [[7,0], [4,4], [7,1], [5,0], [6,1], [5,2]] Output: [[5,0], [7,0], [5,2], [6,1], [4,4], [7,1]]
这是第一次做,没做出来,主要是Arrays.sort()方法的排序不熟悉,也不知道LinkedList插入相同下边元素时候,元素直接后移,就是对插入时候的机制不太了解,这个得回头看一下,具体的解法和详细的解释如下:

public class Solution { /** * 复杂度O(nlogn) * 首先按照身高进行降序排序,身高相同的按照k升序排序 * [[7,0], [4,4], [7,1], [5,0], [6,1], [5,2]] 排序后变为[[7,0], [7,1], [6,1], [5,0], [5,2], [4,4]] * 然后将元素插入到一个LinkedList中,LinkedList每个元素都保存了前后元素的应用,插入和删除快。 * 插入的位置就是离res开始位置偏移了元素第二个元素的位置 * people: [7,0],插入到离开始位置偏移了0个距离的位置。 res: [[7,0]] * people: [7,1],插入到离开始位置偏移了1个距离的位置,即插入到[7,0]的后面。 res: [[7,0], [7,1]] * people: [6,1],插入到离开始位置偏移了1个距离的位置,即插入到[7,0]的后面。 res: [[7,0], [6,1], [7,1]] * people: [5,0],插入到离开始位置偏移了0个距离的位置,即插入到[7,0]的前面。 res: [[5,0], [7,0], [6,1], [7,1]] * people: [5,2],插入到离开始位置偏移了2个距离的位置,即插入到[7,0]的后面。 res: [[5,0], [7,0], [5,2], [6,1], [7,1]] * people: [4,4],插入到离开始位置偏移了4个距离的位置,即插入到[6,1]的后面。 res: [[5,0], [7,0], [5,2], [6,1], [4,4], [7,1]] * @param people * @return res */ public int[][] reconstructQueue(int[][] people) { if (people.length == 0 || people == null || people[0].length == 0) { return new int[0][0]; } Arrays.sort(people, new Comparator<int[]>() { public int compare(int[] o1, int[] o2) { return o1[0] != o2[0] ? -o1[0] + o2[0] : o1[1] - o2[1]; } }); List<int[]> res = new LinkedList<>(); for (int[] ans : people) { res.add(ans[1], ans); } return res.toArray(new int[people.length][]); } }
---------------------------------------------------------------------------------------------------------------------------------
2017/4/2
33. Search in Rotated Sorted Array

Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand. (i.e., 0 1 2 4 5 6 7 might become 4 5 6 7 0 1 2). You are given a target value to search. If found in the array return its index, otherwise return -1. You may assume no duplicate exists in the array.
这个题目解得时候,首先查找mid下标元素的值,判断nums[mid]是否等于target,如果是,返回1;如果不是的话就与low位置的值相比较,判断nums[low]<nums[mid],如果是,那么这个范围内的数字是单调递增的,如果不是,那么这个范围内的数字不是单调的。如果是单调递增的,那么判断这个nums[low]<=target<=nums[mid],是的话那么让high=mid,否则的话low=mid+1,;如果不是单调递增的话,那么判断nums[mid]=<target<=nums[high],如果是的话,令low=mid,否则的话让high=mid-1。由于区间是low+1<high,所以最后要对结果进行验证,判断low和high哪一个符合要求,具体代码如下:

public class Solution { public int search(int[] nums, int target) { if (nums.length == 0 || nums == null) { return -1; } int low = 0; int high = nums.length - 1; while(low + 1 < high) { int mid = low + ((high - low) >> 1); if (nums[mid] == target) { return mid; } if (nums[mid] > nums[low]) {//前半部分是升序 if (target >= nums[low] && target <= nums[mid]) {//待查找的元素再升序子序列中 high = mid; } else { low = mid + 1; } } else if (nums[mid] < nums[low]){//前半部分不是升序 if (target >= nums[mid] && target <= nums[high]) { low = mid; } else { high = mid - 1; } } } if (nums[low] == target) { return low; } if (nums[high] == target) { return high; } return -1; } }
---------------------------
81. Search in Rotated Sorted Array II

Follow up for "Search in Rotated Sorted Array": What if duplicates are allowed? Would this affect the run-time complexity? How and why? Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand. (i.e., 0 1 2 4 5 6 7 might become 4 5 6 7 0 1 2). Write a function to determine if a given target is in the array. The array may contain duplicates.
旋转数组中存在重复元素的时候,这个时候与上面基本相似,就是加一个判断如果nums[mid]=nums[low]的话,就是让low++,具体代码如下:

public class Solution { public boolean search(int[] nums, int target) { if (nums.length == 0 || nums == null) { return false; } int low = 0; int high = nums.length - 1; int mid; while (low + 1 < high) { mid = low + ((high - low) >> 1); if (nums[mid] == target) { return true; } if (nums[mid] > nums[low]) { if (nums[low] <= target && target <= nums[mid]) { high = mid; } else { low = mid + 1; } } else if (nums[mid] < nums[low]) { if (nums[mid] <= target && target <= nums[high]) { low = mid; } else { high = mid - 1; } } else { low++; } } if (nums[low] == target || nums[high] == target) { return true; } return false; } }
----------------------------
34. Search for a Range

Given an array of integers sorted in ascending order, find the starting and ending position of a given target value. Your algorithm's runtime complexity must be in the order of O(log n). If the target is not found in the array, return [-1, -1]. For example, Given [5, 7, 7, 8, 8, 10] and target value 8, return [3, 4].
先判断该元素是否在数组中,如果不在返回[-1,-1],否则,先查找下限位置,在查找上限位置,查找下限时直接判断nums[mid]<target是否成立,是的话low=mid+1,查找上限时判断nums[mid]>target是否成立,如果成立high=mid-1,代码如下:

public class Solution { public int[] searchRange(int[] nums, int target) { int[] res = {-1, -1}; if (nums == null || nums.length == 0) { return res; } int mid = binarySearch(nums, target); if (mid < 0) { return res; } int start = mid; while (start >= 0 && nums[start] == target) { start--; } start++; res[0] = start; int end = mid; while (end < nums.length && nums[end] == target) { end++; } end--; res[1] = end; return res; } public int binarySearch(int[] nums, int target) { int idx = -1; int low = 0; int high =nums.length - 1; int mid; while (low <= high) { mid = low + ((high - low) >> 1); if (nums[mid] == target) { idx = mid; break; } else if (nums[mid] > target) { high = mid - 1; } else { low = mid + 1; } } return idx; } }
------------------------------
35. Search Insert Position

Given a sorted array and a target value, return the index if the target is found. If not, return the index where it would be if it were inserted in order. You may assume no duplicates in the array. Here are few examples. [1,3,5,6], 5 → 2 [1,3,5,6], 2 → 1 [1,3,5,6], 7 → 4 [1,3,5,6], 0 → 0
题目非常简单,可以采用闭区间,那么查找到直接返回查找到的mid,否则,返回low即可

public class Solution { public int searchInsert(int[] nums, int target) { if (nums.length == 0 || nums == null) { return 0; } int low = 0; int high = nums.length - 1; int mid; while (low <= high) { mid = low + ((high - low) >> 1); if (nums[mid] == target) { return mid; } else if (nums[mid] > target) { high = mid - 1; } else { low = mid + 1; } } return low; } }
-----------------------------
162. Find Peak Element

A peak element is an element that is greater than its neighbors. Given an input array where num[i] ≠ num[i+1], find a peak element and return its index. The array may contain multiple peaks, in that case return the index to any one of the peaks is fine. You may imagine that num[-1] = num[n] = -∞. For example, in array [1, 2, 3, 1], 3 is a peak element and your function should return the index number 2.
首先如果是单调递减,即nums[i]>nums[i+1],那么就往左边寻找峰值或者i自身就是峰值;如果是单调递增,即nums[i]<nums[i+1],那么就去i右边寻找峰值我们很容易在纸上画出来某个点的四种情况(如下图所示):
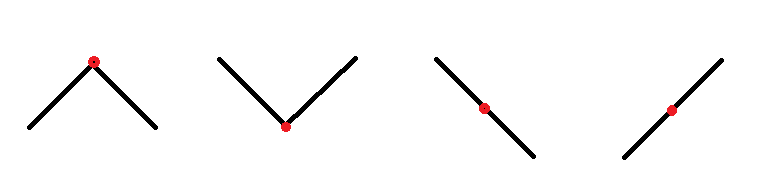
第一种情况:当前点就是峰值,直接返回当前值。
第二种情况:当前点是谷点,不论往那边走都可以找到峰值。
第三种情况:当前点处于下降的中间,往左边走可以到达峰值。
第四种情况:当前点处于上升的中间,往右边走可以达到峰值。
代码如下,由于采用的是开区间low<high,所以在对low和high进行操作的时候要使low=low+1,high=high,即支队low进行加一操作:

public class Solution { public int findPeakElement(int[] nums) { int n = nums.length; if (n == 1) { return 0; } int low = 0; int high = n - 1; int mid; while (low < high) { mid = low + ((high - low) >> 1); if (nums[mid] > nums[mid + 1]) { high = mid; } else { low = mid + 1; } } return low; } }
-------------------------------------------------------------------------------------------------------------------------------
2017/4/6
69. Sqrt(x)

Implement int sqrt(int x). Compute and return the square root of x.
具体的分析可以看一下二分查找总结的博客,代码如下:

public class Solution { public int mySqrt(int x) { if (x == 0 || x == 1) { return x; } else { int start = 0; int end = x; int mid; while (true) { mid = (start + end) / 2; if (mid == x / mid || end - start <= 1) { return mid; } else if (mid < x / mid) { start = mid; } else { end = mid; } } } } }
---------------------------------
50. Pow(x, n)
Implement pow(x, n).
具体代码如下,分析可以看一下总结:

public class Solution { public double myPow(double x, int n) { if (n == 0) { return 1; } else if (n == 1) { return x; } else { if (n > 0) { return pow(x, n); } else { return 1 / pow(x, -n); } } } public double pow(double x, int n) { if (n == 1) { return x; } else { double half = pow(x, n>>>1); if (n % 2 == 0) { return half * half; } else { return half * half * x; } } } }
-------------------------------------------------------------------------------------------------------------------------------------
2017/04/24
70. Climbing Stairs

You are climbing a stair case. It takes n steps to reach to the top. Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top? Note: Given n will be a positive integer.
解析和代码如下:

public class Solution { /** * 当n=1时,方法数为1; * 当n=2时,方法数为2; * 当n=3时,(由于我们只能选择上1层或者2层)我们先选择开始走1层这个方案,剩下两层, * 那么方法数就是n=2的方法数,然后再选择开始走2层这个方案,剩下一层,那么方法数就是n=1的方法数, * 因此n=3时的总方法数就是n=1时的方法数加上n=2时的方法数; * n=4时,先走1层的话,剩下3层,方法数为n=3,先走2层的话,剩下2层,方法数为n=2, * 因此n=4时的总方法数为n=2时的方法数加n=3时的方法数。 * 由此,可发现规律,即是斐波那契数列。 * 设 f (n) 表示爬 n 阶楼梯的不同方法数,为了爬到第 n 阶楼梯,有两个选择:从第 n - 1 阶前进 1 步; * 从第 n - 2 阶前进 2 步;因此,有 f (n) = f (n - 1) + f (n - 2)。 **/ public int climbStairs(int n) { if (n <= 0) { return 0; } int[] dp = new int[n + 1]; dp[0] = 1; dp[1] = 1; for (int i = 2; i<= n; i++) { dp[i] = dp[i - 1] + dp[i - 2]; } return dp[n]; } }
上面的解决方案空间复杂度是O(N),其中大部分空间都是浪费的,因为n的值只与n-1和n-2相关,其中1到n-3的值不需要一直保存着,
可以通过滚动数组的技巧将空间复杂度减少到O(1),代码如下:

public class Solution { public int climbStairs(int n) { if (n <= 2) { return n; } int num0 = 1; int num1 = 1; int res = 0; for (int i = 2; i <= n; i++) { res = num0 + num1; num0 = num1; num1 = res; } return res; } }
-------------------------------------------------------------------------------------------------------------------------------------
523. Continuous Subarray Sum

Given a list of non-negative numbers and a target integer k, write a function to check if the array has a continuous subarray of size at least 2 that sums up to the multiple of k, that is, sums up to n*k where n is also an integer. Example 1: Input: [23, 2, 4, 6, 7], k=6 Output: True Explanation: Because [2, 4] is a continuous subarray of size 2 and sums up to 6. Example 2: Input: [23, 2, 6, 4, 7], k=6 Output: True Explanation: Because [23, 2, 6, 4, 7] is an continuous subarray of size 5 and sums up to 42.
解析和代码如下:

public class Solution { /** * 题目的边界情况比较多,需要注意以下几点: * 子数组长度至少为2; * k可能为0; * n可能为0; * 遍历整个数组,依次加当前数组元素并将相加和与k取余 * 求余结果只有0~k-1这k中情况,将求余结果存入HashTable中 * 如果遍历到当前位置求余结果已经在HashTable中 * 表明从上一求余结果相同的位置到当前位置的子数组相加和是k的倍数 * 否则将求余结果存入HashTable。这里同样需要注意上面提到的边界情况 * 代码中hash[0] = -1这行即为了便于边界情况的处理 **/ public boolean checkSubarraySum(int[] nums, int k) { if (nums == null || nums.length < 2) { return false; } Map<Integer, Integer> map = new HashMap<>(); map.put(0, -1); int sum = 0; for (int i = 0; i < nums.length; i++) { sum += nums[i]; Integer pre = map.get(k == 0 ? sum : sum % k); if (pre != null) { if (i - pre > 1) { return true; } } else { map.put(k == 0 ? sum : sum % k, i); } } return false; } }
-----------------------------------------------------------------------------------------------------------------------------------------
2017/06/29
20. Valid Parentheses

Given a string containing just the characters '(', ')', '{', '}', '[' and ']', determine if the input string is valid.
The brackets must close in the correct order, "()" and "()[]{}" are all valid but "(]" and "([)]" are not.
思路:

用一个Stack来存储括号, 主要考察对栈数据结构的操作。算法的时间复杂度是O(n),空间复杂度也是O(n)。
遍历传入的String s,如果遇到左括号就入栈;如果遇到右括号,检查栈如果为空,证明不能匹配,如果栈不空,pop出栈顶的元素,看是否与当前的右括号匹配。
如果匹配,继续向下进行新一轮的循环,如果不匹配,返回false.
注意:
全部字符都检查完了以后,判断栈是否为空,空则正确都匹配,不空则证明有没匹配的。
检查字符是用==,检查String是用.isEqual(),因为String是引用类型,值相等但是地址可能不等。
具体代码如下:

public class Solution { public boolean isValid(String s) { if (s.length() == 0 || s.length() == 1) { return false; } Stack<Character> stack = new Stack<Character>(); for (int i = 0; i < s.length(); i++) { char cur = s.charAt(i); if (cur == '(' || cur == '[' || cur == '{') { stack.push(cur); } else { switch (cur) { case ')' : if (stack.isEmpty() || stack.pop() != '(') { return false; } break; case ']' : if (stack.isEmpty() || stack.pop() != '[') { return false; } break; case '}' : if (stack.isEmpty() || stack.pop() != '{') { return false; } break; default : break; } } } return stack.isEmpty(); } }
还有一种比较简洁的做法是,先将字符串转化为字符数组,然后遍历数组,当字符是'(','{','[' 时,将 ')','}',']'入栈,否则先判断栈是否为空,如果为空的话,返回false,不为空的话
比较这个字符与stack.pop()的字符是否相等,不是的话返回false,最后要记的判断一下栈是否为空,空的话则正确匹配,否则的话证明有没匹配的。
具体代码如下:

public class Solution { public boolean isValid(String s) { Stack<Character> stack = new Stack<Character>(); for (char cur : s.toCharArray()) { if (cur == '(') { stack.push(')'); } else if (cur == '[') { stack.push(']'); } else if (cur == '{') { stack.push('}'); } else if (stack.isEmpty() || stack.pop() != cur) { return false; } } return stack.isEmpty(); } }
-------------------------------------------------------------------------------------------------------------------------------------------
2017/08/17
2. Add Two Numbers

You are given two non-empty linked lists representing two non-negative integers. The digits are stored in reverse order and each of their nodes contain a single digit. Add the two numbers and return it as a linked list. You may assume the two numbers do not contain any leading zero, except the number 0 itself. Input: (2 -> 4 -> 3) + (5 -> 6 -> 4) Output: 7 -> 0 -> 8
具体思路是创建一个新的链表来存储新的值,每一个节点存储相应节点值的和取余10,注意点是最后可能需要进位,
所以循环的时候要判断carry是否等于0,如果不等于表时有进位,还需要创建新的节点,具体代码如下:

/** * Definition for singly-linked list. * public class ListNode { * int val; * ListNode next; * ListNode(int x) { val = x; } * } */ public class Solution { public ListNode addTwoNumbers(ListNode l1, ListNode l2) { if (l1 == null) { return l2; } if (l2 == null) { return l1; } //创建新的链表 ListNode head = new ListNode(0); ListNode p = head; //存储相加的结果 int carry = 0; //任何一个链表不为空,或者carry != 0,这表示最后有进位 //例如最后为5+5=10,最后carry=1,两个链表都为空了,这是需要 //进位,创建新的节点 while (l1 != null || l2 != null || carry != 0) { //如果为空的话不需要将carry+0,直接不操作 if (l1 != null) { carry += l1.val; l1 = l1.next; } if (l2 != null) { carry += l2.val; l2 = l2.next; } //创建新节点 p.next = new ListNode(carry % 10); p = p.next; carry /= 10; } return head.next; } }
--------------------------------------------------------------------------------------------------------------------------------------------
2017/08/18
445. Add Two Numbers II

You are given two non-empty linked lists representing two non-negative integers. The most significant digit comes first and each of their nodes contain a single digit. Add the two numbers and return it as a linked list. You may assume the two numbers do not contain any leading zero, except the number 0 itself. Follow up: What if you cannot modify the input lists? In other words, reversing the lists is not allowed. Example: Input: (7 -> 2 -> 4 -> 3) + (5 -> 6 -> 4) Output: 7 -> 8 -> 0 -> 7
有两种解法,首先第一种是跟上一题类似,所以要先将链表反转,然后在利用上一道题的思路进行相加,
最后将结果进行反转后返回,具体代码如下:

/** * Definition for singly-linked list. * public class ListNode { * int val; * ListNode next; * ListNode(int x) { val = x; } * } */ public class Solution { public ListNode addTwoNumbers(ListNode l1, ListNode l2) { if (l1 == null) { return l2; } if (l2 == null) { return l1; } l1 = recursive(l1); l2 = recursive(l2); ListNode head = new ListNode(0); ListNode phead = head; int tmp = 0; while (l1 != null || l2 != null || tmp != 0) { if (l1 != null) { tmp += l1.val; l1 = l1.next; } if (l2 != null) { tmp += l2.val; l2 = l2.next; } phead.next = new ListNode(tmp % 10); phead = phead.next; tmp /= 10; } return recursive(head.next); } public ListNode recursive(ListNode head) { if (head == null || head.next == null) { return head; } ListNode pre = head; ListNode p = head.next; ListNode next = null; while (p != null) { next = p.next; p.next = pre; pre = p; p = next; } head.next = null; return pre; } }
还有一种是不需要反转链表,利用栈进行计算,首先将两个链表中的元素都入栈,然后出栈进行相加。所以要声明一个节点head,
然后进行循环,每次将head节点的值重新赋为carry%10,然后重新声明一个节点p,指向head,然后head = p,这样下一次循环
的时候就可以再指向head节点了,p节点的值是carry/10,因为假如最后需要进位的话,p就是进位的节点,不需要进位的话p节点的
值就是0,最后返回的时候判断一下就行了,不能将0也返回。具体代码如下:

/** * Definition for singly-linked list. * public class ListNode { * int val; * ListNode next; * ListNode(int x) { val = x; } * } */ class Solution { public ListNode addTwoNumbers(ListNode l1, ListNode l2) { if (l1 == null) { return l2; } if (l2 == null) { return l1; } Stack<Integer> s1 = new Stack<Integer>(); Stack<Integer> s2 = new Stack<Integer>(); while (l1 != null) { s1.push(l1.val); l1 = l1.next; } while (l2 != null) { s2.push(l2.val); l2 = l2.next; } ListNode head = new ListNode(0); int carry = 0; while (!s1.isEmpty() || !s2.isEmpty()) { if (!s1.isEmpty()) { carry += s1.pop(); } if (!s2.isEmpty()) { carry += s2.pop(); } head.val = carry % 10; ListNode p = new ListNode(carry / 10); p.next = head; head = p; carry /= 10; } return head.val == 0 ? head.next : head; } }
----------------------
328. Odd Even Linked List

Given a singly linked list, group all odd nodes together followed by the even nodes. Please note here we are talking about the node number and not the value in the nodes. You should try to do it in place. The program should run in O(1) space complexity and O(nodes) time complexity. Example: Given 1->2->3->4->5->NULL, return 1->3->5->2->4->NULL. Note: The relative order inside both the even and odd groups should remain as it was in the input. The first node is considered odd, the second node even and so on ...
保存偶节点的第一个节点,然后将奇数节点的next指向奇数节点next.next节点,也就是下一个奇数节点,偶数节点同理
最后将奇数节点的next指向偶数节点的第一个节点,注意循环的条件,even!=null&&even.next!=null,也就是当前的偶数节点
和奇数节点不为空,如果为空的话.next就没有意义了,具体代码如下:

/** * Definition for singly-linked list. * public class ListNode { * int val; * ListNode next; * ListNode(int x) { val = x; } * } */ class Solution { public ListNode oddEvenList(ListNode head) { if (head == null || head.next == null) { return head; } ListNode odd = head; ListNode even = head.next; ListNode peven = even; while (even != null && even.next != null) { odd.next = odd.next.next; even.next = even.next.next; odd = odd.next; even = even.next; } odd.next = peven; return head; } }
-------------------------------------------------------------------------------------------------------------
2017/08/19
lintcode 372.在O(1)时间复杂度删除链表节点

给定一个单链表中的一个等待被删除的节点(非表头或表尾)。请在在O(1)时间复杂度删除该链表节点。
样例
Linked list is 1->2->3->4, and given node 3, delete the node in place 1->2->4
一般情况下删除链表节点需要知道该节点的前一个节点,但是这样的话时间复杂度就变为O(n)了,所以看题目知道该节点非表头或者表尾,
所以直接获取该节点的下一个节点,将该节点的值赋为下一个节点的值,该节点的next指针赋为下一个节点的next,这样就能在O(1)的
时间内实现删除节点,当删除的节点是前n-1个节点时都可以这样做,当是最后一个时,必须获取前一个节点,这是时间复杂度是O(n),
但是总的时间复杂度是(O(1)*(n-1) + O(n)*1)/n = O(1),具体代码如下:

/** * Definition for ListNode. * public class ListNode { * int val; * ListNode next; * ListNode(int val) { * this.val = val; * this.next = null; * } * } */ public class Solution { /** * @param node: the node in the list should be deleted * @return: nothing */ public void deleteNode(ListNode node) { // write your code here //如果删除节点为前面的n-1个节点, //则时间复杂度为O(1), //只有删除节点为最后一个时, //时间复杂度才为O(n), //所以平均的时间复杂度为:(O(1) * (n-1) + O(n))/n = O(1); //仍然为O(1) ListNode next = node.next; node.val = next.val; node.next = next.next; } }
---------------------------------
138. Copy List with Random Pointer

A linked list is given such that each node contains an additional random pointer which could point to any node in the list or null. Return a deep copy of the list.
题目对时间复杂度没有要求,第一种解法,就是创建一个map,key是旧的节点,value是新的节点,首先遍历旧节点,
同时利用旧节点的label创建新的节点,然后给新节点的random和next赋值,所以要再遍历一遍旧节点,得到新的节点,然后新节点
的next的值为map当中当前旧的节点cur的cur.next在map中所对应的值,也就是map.get(cur).next = map.get(cur.next),同理新节点
的random也是这样做,map.get(cur).random = map.get(cur.random),这样时间复杂度和空间复杂度都是O(n),代码如下:

/** * Definition for singly-linked list with a random pointer. * class RandomListNode { * int label; * RandomListNode next, random; * RandomListNode(int x) { this.label = x; } * }; */ public class Solution { public RandomListNode copyRandomList(RandomListNode head) { if (head == null) { return head; } HashMap<RandomListNode, RandomListNode> map = new HashMap<RandomListNode, RandomListNode>(); RandomListNode p = head; while (p != null) { map.put(p, new RandomListNode(p.label)); p = p.next; } p = head; while (p != null) { map.get(p).next = map.get(p.next); map.get(p).random = map.get(p.random); p = p.next; } return map.get(head); } }
另一种解法是创建一个新的链表,将新节点插入到旧结点后面,这样的话next的值就不用特意去赋值了,需要赋random的值,
这是直接遍历一遍旧的链表将旧节点的random值赋值给新节点就行,最后将旧节点和新节点拆开,这样的话时间复杂度是O(n),
空间复杂度变成了O(1),具体代码如下:

/** * Definition for singly-linked list with a random pointer. * class RandomListNode { * int label; * RandomListNode next, random; * RandomListNode(int x) { this.label = x; } * }; */ public class Solution { public RandomListNode copyRandomList(RandomListNode head) { if (head == null) { return head; } //首先创建一个新的链表,将复制的节点插入到旧节点的后面 RandomListNode cur = head; RandomListNode next = null; while (cur != null) { next = cur.next; RandomListNode copy = new RandomListNode(cur.label); cur.next = copy; copy.next = next; cur = next; } //将random指针赋值给新的节点 cur = head; while (cur != null) { if (cur.random != null) { //新的节点的random指向旧节点random所指向节点的下一个节点 cur.next.random = cur.random.next; } cur = cur.next.next; } //将链表拆开,将新的链表拆出来 cur = head; RandomListNode phead = new RandomListNode(0); RandomListNode p = phead; RandomListNode oldnext = null; RandomListNode newnext = null; while (cur != null) { //拆开新的节点 newnext = cur.next; p.next = newnext; p = newnext; //拆开旧的节点 oldnext = cur.next.next; cur.next = oldnext; cur = oldnext; } return phead.next; } }
--------------------------------
lintcode 511交换链表当中两个节点

给你一个链表以及两个权值v1和v2,交换链表中权值为v1和v2的这两个节点。保证链表中节点权值各不相同,如果没有找到对应节点,那么什么也不用做。 注意事项 你需要交换两个节点而不是改变节点的权值 样例 给出链表 1->2->3->4->null ,以及 v1 = 2 , v2 = 4 返回结果 1->4->3->2->null。
首先找到这两个节点,以及这两个节点的前面的节点,然后进行交换就行,需要注意的是当两个节点相邻时,需要特殊处理,
还有v1和v2的节点前后顺序不一定,有可能v2所对应节点在v1前面,这个需要判断,代码如下:

public class Solution { /* * @param head: a ListNode * @param v1: An integer * @param v2: An integer * @return: a new head of singly-linked list */ public ListNode swapNodes(ListNode head, int v1, int v2) { // write your code here if (head == null || head.next == null || v1 == v2) { return head; } ListNode node1 = search(head, v1); ListNode node2 = search(head, v2); if (node1 == null || node2 == null) { return head; } ListNode phead = new ListNode(0); phead.next = head; ListNode pre = phead; ListNode pre1 = null; ListNode pre2 = null; while (pre != null) { if (pre.next == node1) { pre1 = pre; } if (pre.next == node2) { pre2 = pre; } pre = pre.next; } //v1在v2的前面 if (pre2 == node1) { node1.next = node2.next; pre1.next = node2; node2.next = node1; } else if (pre1 == node2) {//v2在v1的前面 node2.next = node1.next; pre2.next = node1; node1.next = node2; } else { ListNode next2 = node2.next; node2.next = node1.next; node1.next = next2; pre1.next = node2; pre2.next = node1; } return phead.next; } public ListNode search(ListNode head, int v) { ListNode p = head; ListNode cur = null; while (p != null) { if (p.val == v) { cur = p; break; } p = p.next; } return cur; } };
----------------------------------------------------------------------------------------------------------------
2017/08/21
155. Min Stack

Design a stack that supports push, pop, top, and retrieving the minimum element in constant time. push(x) -- Push element x onto stack. pop() -- Removes the element on top of the stack. top() -- Get the top element. getMin() -- Retrieve the minimum element in the stack. Example: MinStack minStack = new MinStack(); minStack.push(-2); minStack.push(0); minStack.push(-3); minStack.getMin(); --> Returns -3. minStack.pop(); minStack.top(); --> Returns 0. minStack.getMin(); --> Returns -2.
这道题的关键就是获得当前栈的最小值,如果是单纯的在每次入栈的时候比较一下,然后记录下当前最小值的话,那么当出栈
的是当前的最小值的话,就无法获取剩余数据里面的最小值了,所以在入栈的时候,如果入栈的元素比当前最小值小,那么
首先将当前最小值入栈,然后改变最小值的值,然后再将新的最小值入栈,这样最小值下面就是第二小的值,当最小值出栈时,
剩余元素的最小值就是出栈元素的下一个元素,具体代码如下:

class MinStack { //min用于保存当前的最小值 int min = Integer.MAX_VALUE; Stack<Integer> stack; /** initialize your data structure here. */ public MinStack() { stack = new Stack<Integer>(); } public void push(int x) { //如果当前入栈的值小于当前的最小值, //那么首先将当前的最小值,也就是第二小的值入栈,然后令min=当前最小值 //然后再将当前最小的值入栈 //如果没有min的话,在出栈的时候如果弹出的是当前的最小值,那么就没法得到 //剩余的数据里面哪一个是最小的,所以如果是最小,先将第二小的入栈,再将最小入栈 //那么当最小的出栈时,就能获得剩余的数据中最小的数了 if (x <= min) { stack.push(min); min = x; } stack.push(x); } public void pop() { //首先是执行stack.pop(),所以无论怎么样,都执行了一次pop操作, //如果当前pop的值是最小值,那么它的下一个值一定是第二小的, //当最小值出栈后,剩余数据中的最小值一定是它的下一个,直接令min=stack.pop() if (stack.pop() == min) { min = stack.pop(); } //如果min改变过,那么在栈为空的时候要将min改变回来 if (stack.isEmpty()) { min = Integer.MAX_VALUE; } } public int top() { return stack.peek(); } public int getMin() { return min; } } /** * Your MinStack object will be instantiated and called as such: * MinStack obj = new MinStack(); * obj.push(x); * obj.pop(); * int param_3 = obj.top(); * int param_4 = obj.getMin(); */
--------------------------------
225. Implement Stack using Queues

Implement the following operations of a stack using queues. push(x) -- Push element x onto stack. pop() -- Removes the element on top of the stack. top() -- Get the top element. empty() -- Return whether the stack is empty. Notes: You must use only standard operations of a queue -- which means only push to back, peek/pop from front, size, and is empty operations are valid. Depending on your language, queue may not be supported natively. You may simulate a queue by using a list or deque (double-ended queue), as long as you use only standard operations of a queue. You may assume that all operations are valid (for example, no pop or top operations will be called on an empty stack).
创建一个队列,每次插入新值之后,都将新值前面的所有数据反转,这样新插入的值就位于头部了,具体的做法是每次都push进
pop的元素,直到最后一个元素,其余的操作就好做了,具体代码如下:

class MyStack { Queue<Integer> queue; /** Initialize your data structure here. */ public MyStack() { queue = new LinkedList<Integer>(); } /** Push element x onto stack. */ public void push(int x) { queue.offer(x); //反转已经加入的元素,这样最新加入的元素就跑到队列头上去了,这样就能模拟栈了 for (int i = 0; i < queue.size() - 1; i++) { queue.offer(queue.poll()); } } /** Removes the element on top of the stack and returns that element. */ public int pop() { return queue.poll(); } /** Get the top element. */ public int top() { return queue.peek(); } /** Returns whether the stack is empty. */ public boolean empty() { return queue.isEmpty(); } } /** * Your MyStack object will be instantiated and called as such: * MyStack obj = new MyStack(); * obj.push(x); * int param_2 = obj.pop(); * int param_3 = obj.top(); * boolean param_4 = obj.empty(); */
----------------------------------
232. Implement Queue using Stacks

Implement the following operations of a queue using stacks. push(x) -- Push element x to the back of queue. pop() -- Removes the element from in front of queue. peek() -- Get the front element. empty() -- Return whether the queue is empty. Notes: You must use only standard operations of a stack -- which means only push to top, peek/pop from top, size, and is empty operations are valid. Depending on your language, stack may not be supported natively. You may simulate a stack by using a list or deque (double-ended queue), as long as you use only standard operations of a stack. You may assume that all operations are valid (for example, no pop or peek operations will be called on an empty queue).
创建两个栈,每次执行push操作时,先将stack1中的元素pop并push到stack2中,然后再将新的元素push到stack2中,
然后再将stack2中所有的元素都pop并push到stack1中,这样的话最新的元素总是在最底下,
最开始插入的元素总是在栈顶,这样就能模拟队列了,具体代码如下:

class MyQueue { Stack<Integer> stack1; /** Initialize your data structure here. */ public MyQueue() { stack1 = new Stack<Integer>(); } /** Push element x to the back of queue. */ public void push(int x) { Stack<Integer> stack2 = new Stack<Integer>(); while (!stack1.isEmpty()) { stack2.push(stack1.pop()); } stack2.push(x); while (!stack2.isEmpty()) { stack1.push(stack2.pop()); } } /** Removes the element from in front of queue and returns that element. */ public int pop() { return stack1.pop(); } /** Get the front element. */ public int peek() { return stack1.peek(); } /** Returns whether the queue is empty. */ public boolean empty() { return stack1.isEmpty(); } } /** * Your MyQueue object will be instantiated and called as such: * MyQueue obj = new MyQueue(); * obj.push(x); * int param_2 = obj.pop(); * int param_3 = obj.peek(); * boolean param_4 = obj.empty(); */
-------------------------------------------------------------------------------------------------------------
2017/09/05
71. Simplify Path

Given an absolute path for a file (Unix-style), simplify it. For example, path = "/home/", => "/home" path = "/a/./b/../../c/", => "/c" click to show corner cases. Corner Cases: Did you consider the case where path = "/../"? In this case, you should return "/". Another corner case is the path might contain multiple slashes '/' together, such as "/home//foo/". In this case, you should ignore redundant slashes and return "/home/foo".
具体思路和代码如下:

class Solution { /** *首先对字符串根据'/'进行分割 *这样分割的结果是:. .. 正常字符串 空字符 *如果遇到的是空字符或者是.,那么什么也不做 *如果遇到的是..,那么需要返回上一级目录,如果栈不为空,那么栈中的元素出栈,否则的话直接不操作,因为没有上级目录了 *如果遇到的是正常字符,那么直接入栈 *最后判断栈是否为空,如果为空,说明在根目录下,返回/ *否则拼接字符串,注意最先出栈的元素位于后面,中间加上/分隔开,返回结果 */ public String simplifyPath(String path) { if (path.length() == 0 || path == null) { return path; } Stack<String> stack = new Stack<String>(); String[] array = path.split("/"); String res = ""; for (int i = 0; i < array.length; i++) { if (array[i].equals("") || array[i].equals(".")) { } else if (array[i].equals("..")) { if (!stack.isEmpty()) { stack.pop(); } } else { stack.push(array[i]); } } if (stack.isEmpty()) { return "/"; } while (!stack.isEmpty()) { res = "/" + stack.pop() + res; } return res; } }
------------------------------------
42. Trapping Rain Water
Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.
For example,
Given [0,1,0,2,1,0,1,3,2,1,2,1], return 6.

The above elevation map is represented by array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rain water (blue section) are being trapped. Thanks Marcosfor contributing this image!
解题思路:
思路一:开辟两个数组空间,逐个遍历数组,找出该位置左边的最大值与右边的最大值,分别放到两个数组中。然后对整个数组进行遍历,位置装水后的值不能超过该位置左右最高值中的最小数。该算法需三次遍历数组,但是时间复杂度为O(n);空间需开辟两个数组空间,空间复杂度为O(n)。具体代码如下:

class Solution { public int trap(int[] height) { if (height == null || height.length == 0) { return 0; } int res = 0; int length = height.length; int[] leftMax = new int[length]; int[] rightMax = new int[length]; int tmp = 0; //找到当前位置左边的最大值 for (int i = 0; i < length; i++) { leftMax[i] = tmp; tmp = Math.max(tmp, height[i]); } tmp = 0; //找到当前位置右边的最大值 for (int i = length - 1; i >= 0; i--) { rightMax[i] = tmp; tmp = Math.max(tmp, height[i]); } //遍历数组,找到当前位置左右最大的值中的最小值,然后计算与当前位置的差值,即为当前位置所能装的水的高度 for (int i = 0; i < length; i++) { tmp = Math.min(leftMax[i], rightMax[i]); if (tmp >= height[i]) { res += tmp - height[i]; } } return res; } }
思路二:
设置两个指示变量,分别存放当前指向的两个位置。找出左位置的左边的最高值和右位置的右边的最高值。对于两者中的最小值,表明当前位置加上水过后的值不超出该值,那么相减即可,反之,对另一个相减。该算法只需要一次遍历数组,所以效率更高,时间复杂度为O(n);空间方面不需要开辟数组空间,所以为常数空间。具体代码如下:

class Solution { public int trap(int[] height) { if (height == null || height.length == 0) { return 0; } int length = height.length; int left = 0; int right = length - 1; int leftMax = 0; int rightMax = 0; int res = 0; //创建双指针,初始时分别指向两头 //找出左位置左边的最高值和右位置右边的最高值 //对于两个中的最小值,当前位置加上水之后不超过这个最小值 //所以利用这个最小值减去当前高度即可 //如果是左边的小,则left++,如果右边的小,则right++ //只需遍历一遍数组,时间复杂度O(n),空间复杂度为O(1) while (left < right) { leftMax = Math.max(leftMax, height[left]); rightMax = Math.max(rightMax, height[right]); if (leftMax < rightMax) { res += leftMax - height[left]; left++; } else { res += rightMax - height[right]; right--; } } return res; } }
---------------------------------------------------------------------------------------
2017/09/11
84. Largest Rectangle in Histogram
Given n non-negative integers representing the histogram's bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

The largest rectangle is shown in the shaded area, which has area = 10 unit.
For example,
Given heights = [2,1,5,6,2,3],
return 10.
解题思路:

假设当前位置值为cur,其左边第一个比cur小得下标为l, 右边第一个比cur小的元素下标为r, 那么这中间的最大值就是(r-l+1)*heights[cur] 现在假设数组是升序的,那么r=cur,只需寻找左边 元素的下标l就行了,具体的思路如下: 1、如果已知height数组是升序的,应该怎么做? 比如1,2,5,7,8 那么就是(1*5) vs. (2*4) vs. (5*3) vs. (7*2) vs. (8*1) 也就是max(height[i]*(size-i)) 2、使用栈的目的就是构造这样的升序序列,按照以上方法求解。 但是height本身不一定是升序的,应该怎样构建栈? 比如2,1,5,6,2,3 (1)2进栈。s={2}, result = 0 (2)1比2小,不满足升序条件,因此将2弹出,并记录当前结果为2*1=2。 将2替换为1重新进栈。s={1,1}, result = 2 (3)5比1大,满足升序条件,进栈。s={1,1,5},result = 2 (4)6比5大,满足升序条件,进栈。s={1,1,5,6},result = 2 (5)2比6小,不满足升序条件,因此将6弹出,并记录当前结果为6*1=6。s={1,1,5},result = 6 2比5小,不满足升序条件,因此将5弹出,并记录当前结果为5*2=10(因为已经弹出的5,6是升序的)。s={1,1},result = 10 2比1大,将弹出的5,6替换为2重新进栈。s={1,1,2,2,2},result = 10 (6)3比2大,满足升序条件,进栈。s={1,1,2,2,2,3},result = 10 栈构建完成,满足升序条件,因此按照升序处理办法得到上述的max(height[i]*(size-i))=max{3*1, 2*2, 2*3, 2*4, 1*5, 1*6}=8<10 综上所述,result=10
代码如下:

class Solution { public int largestRectangleArea(int[] heights) { if (heights == null || heights.length == 0) { return 0; } Stack<Integer> stack = new Stack<Integer>(); int res = 0; for (int i = 0; i < heights.length; i++) { if (stack.isEmpty() || stack.peek() < heights[i]) { stack.push(heights[i]); } else { int count = 0; while (!stack.isEmpty() && heights[i] < stack.peek()) { count++; res = Math.max(res, stack.pop() * count); } while (count-- >= 0) { stack.push(heights[i]); } } } int count = 1; while (!stack.isEmpty()) { res = Math.max(res, stack.pop() * count); count++; } return res; } }
-------------------------------------------------------------------------
2017/09/12
85. Maximal Rectangle

Given a 2D binary matrix filled with 0's and 1's, find the largest rectangle containing only 1's and return its area. For example, given the following matrix: 1 0 1 0 0 1 0 1 1 1 1 1 1 1 1 1 0 0 1 0 Return 6.
假设把矩阵沿着某一行分开,然后把分开的行作为底面,将自底面往上的矩阵看成一个直方图(histogram)。直方图的中每个项的高度就是从底面行开始往上1的数量。根据Largest Rectangle in Histogram就可以求出当前行作为矩阵下边缘的一个最大矩阵。接下来如果对每一行都做一次Largest Rectangle in Histogram,从其中选出最大的矩阵,那么它就是整个矩阵中面积最大的子矩阵。
如何计算某一行为底面时直方图的高度呢?如果重新计算,那么每次需要的计算数量就是当前行数乘以列数。然而会发现一些动态规划的踪迹,如果知道上一行直方图的高度,就只需要看新加进来的行(底面)上对应的列元素是不是0,如果是,则高度是0,否则则是上一行直方图的高度加1。利用历史信息,就可以在线行时间内完成对高度的更新。由于Largest Rectangle in Histogram的算法复杂度是O(n)。所以完成对一行为底边的矩阵求解复杂度是O(n+n)=O(n)。接下来对每一行都做一次,那么算法总时间复杂度是O(m*n)。
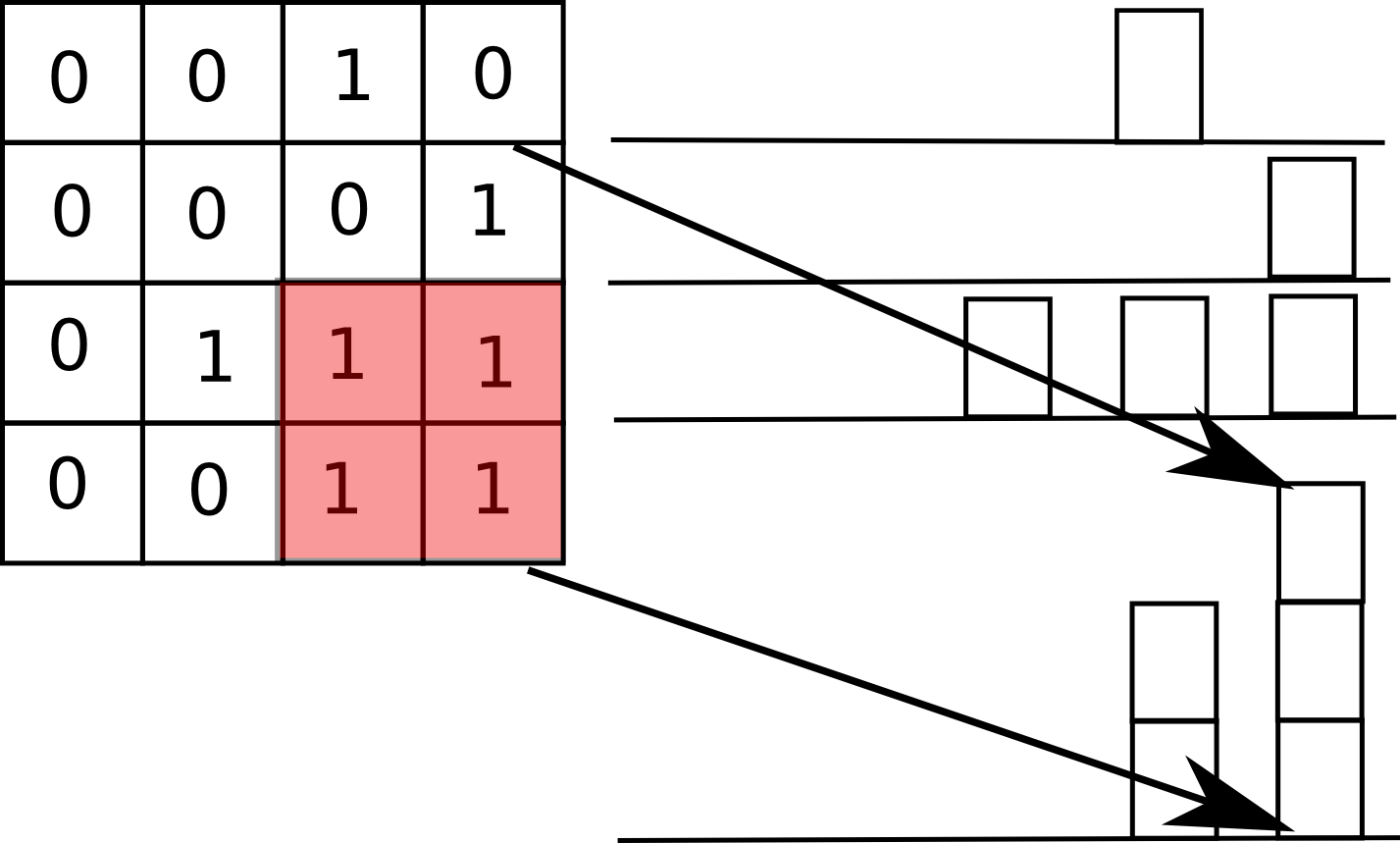
上面的矩阵就成这样了:
时间复杂度:O(mn)
空间复杂度:O(n)
具体代码如下:

class Solution { public int maximalRectangle(char[][] matrix) { if (matrix.length == 0 || matrix[0].length == 0) { return 0; } int res = 0; int row = matrix.length; int col = matrix[0].length; //tmp数组存储以该行为底,上面每列有多少个1 int[] tmp = new int[col]; for (int i = 0; i < row; i++) { for (int j = 0; j < col; j++) { tmp[j] = matrix[i][j] == '0' ? 0 : tmp[j] + 1; } res = Math.max(res, largestRectangleArea(tmp)); } return res; } public int largestRectangleArea(int[] heights) { if (heights == null || heights.length == 0) { return 0; } Stack<Integer> stack = new Stack<Integer>(); int res = 0; for (int i = 0; i < heights.length; i++) { if (stack.isEmpty() || stack.peek() < heights[i]) { stack.push(heights[i]); } else { int count = 0; while (!stack.isEmpty() && heights[i] < stack.peek()) { count++; res = Math.max(res, stack.pop() * count); } while (count-- >= 0) { stack.push(heights[i]); } } } int count = 1; while (!stack.isEmpty()) { res = Math.max(res, stack.pop() * count); count++; } return res; } }
-------------------------------------------------

