堆排序

堆排序

堆

（二叉）堆是一种具有特殊性质的二叉树。要么所有结点都大于它的左右孩子结点，要么所有结点都小于它的左右孩子结点。前者被称为大根堆，后者被称为小根堆。如图：

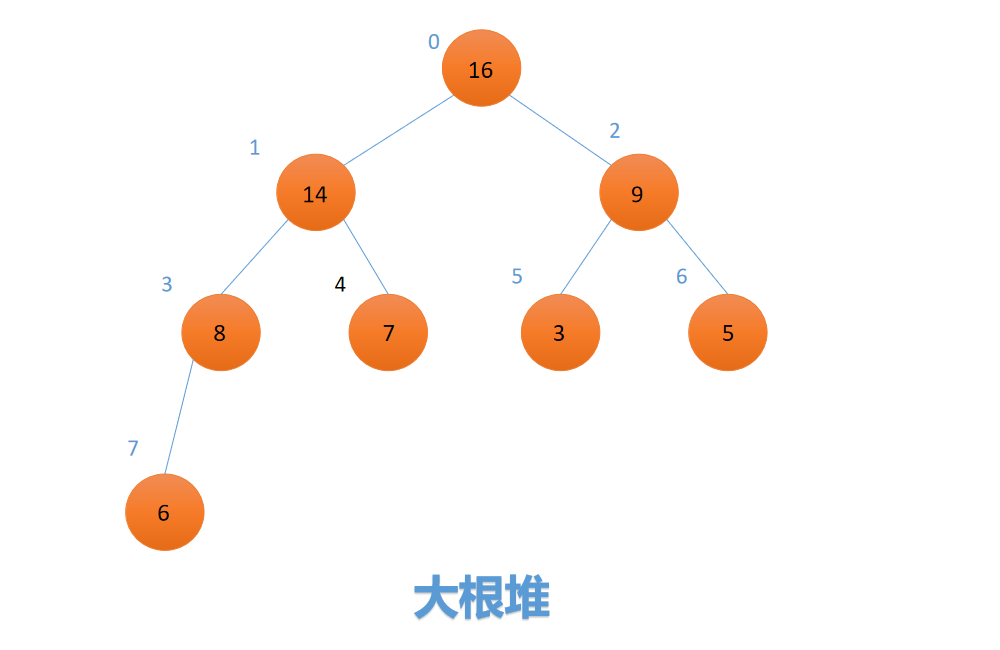
从上到下，左到右编号序号后，我们可以用一个数组来表示这种结构（箭头指向的是孩子结点），即：

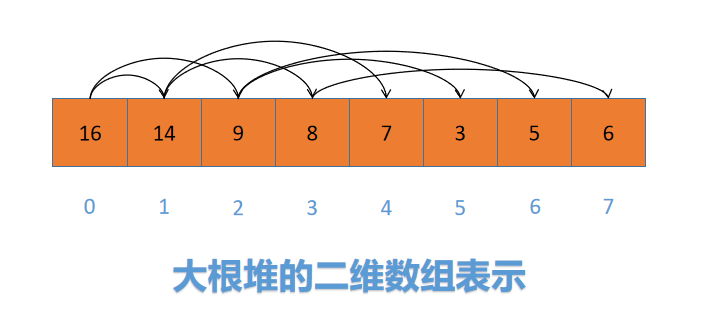
如果从0开始编号的话，可以发现，如果一个结点的下标为[i]，则它的左孩子和右孩子的下标分别为：[2i+1]和 [2i+2]。

把该数组记为 A 则大根堆的性质可以归纳为：

[A[i]geq max(A[2i+1],A[2i+2]) ]

容易得出，小根堆的性质是：

[A[i]leq min(A[2i+1],A[2i+2]) ]

维护堆的性质

现在考虑这样的一种情况。比如说，我把刚刚的那个大根堆的根16换成4，这就违背了大根堆的性质，它就不是一个大根堆了，像这样：

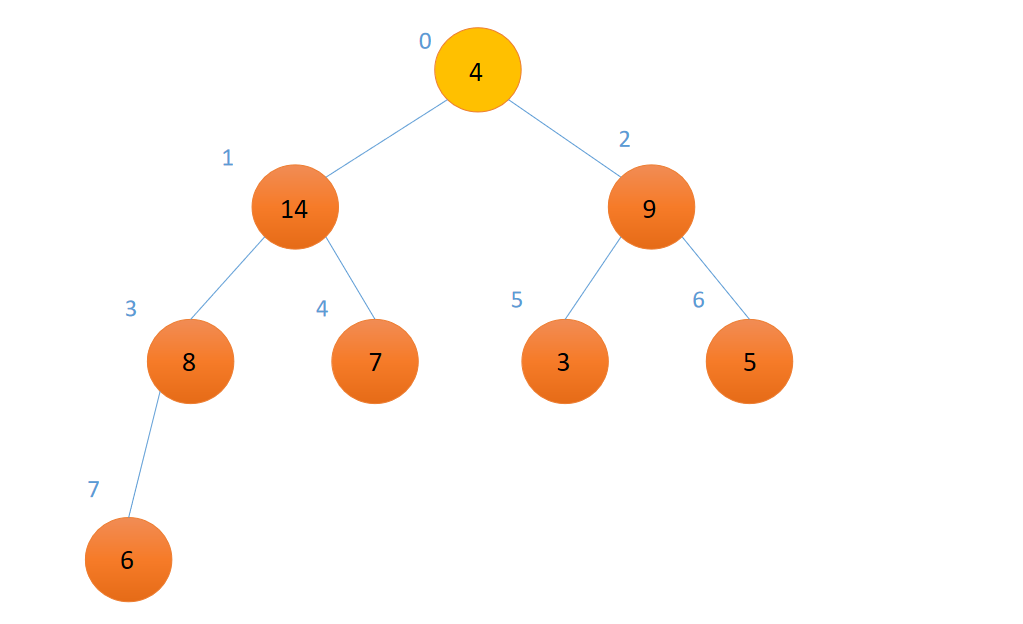
而我们要让它（以4为根结点的树）保持大根堆的性质，所以，我们要让这个4这个节点，在堆里面逐级下降。具体来讲是，比较当前结点和它的孩子结点的值，若孩子结点的值比它要大，则和最大的孩子结点做交换，否则不交换。交换之后，由于比较小的那个结点往下走了，所以可能会导致下面的子树违背了大根堆的性质，所以要对子树递归的进行这个操作，直到那个以指定的结点为根的子树满足大根堆的性质。

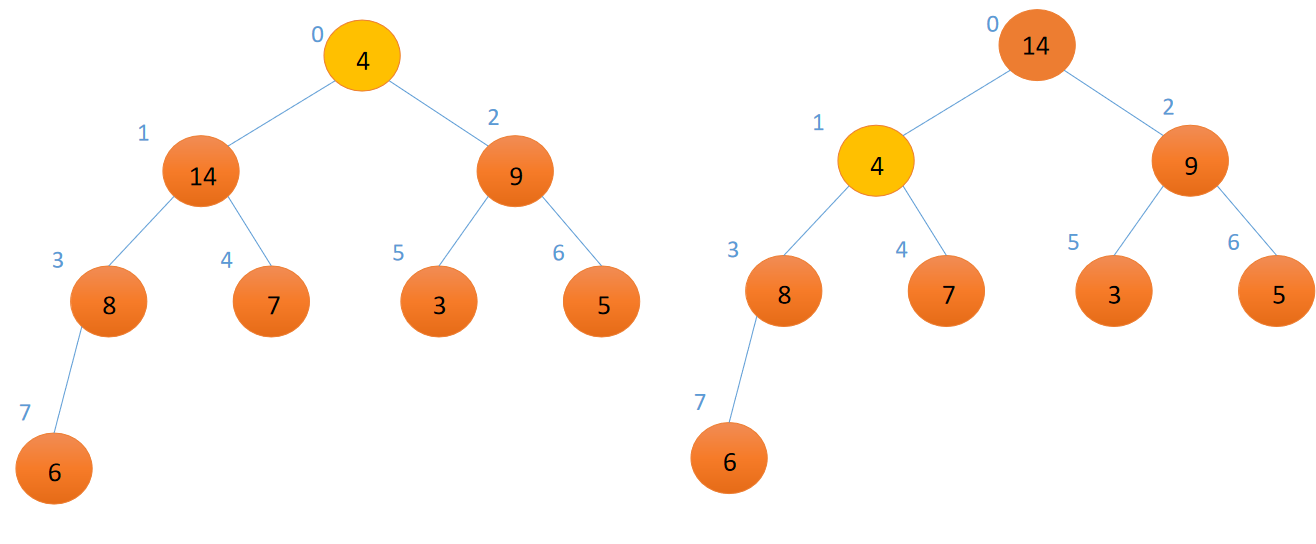
显然，我们很容易看到，经过调整之后，这个树依然是一个大根堆。但实际上，并不是所有情况都是如此的，因为这里替换的是大根堆堆顶的一个元素，并且从它开始进行调整。如果原本就不是一个大根堆，那经过一次调整后的结果就不一定是大根堆。

把这过程写成一个函数就是：

//维护最大堆的性质
void max_heapify(int *A, int i, int size) {
	int L = i * 2 + 1;  //左孩子下标(默认下标从0开始）
	int R = i * 2 + 2; //右孩子下标
	int largest = i;   //记住i和i的左右孩子三者中最大的那个的下标
	if (L < size && A[L] > A[largest]) {
		largest = L;
	}
	if (R < size && A[R] > A[largest]) {
		largest = R;
	}
	//如果违背了最大堆的性质，则交换
	if (largest != i) {
		swap(A[largest], A[i]);
		//递归进行调整
		max_heapify(A, largest, size);
	}
}

建堆

我们怎么从把原本杂乱无章的数据建成一个堆呢？

上面可以看到，如果某个结点为根的子树都满足大根堆的性质的话，那么从这个根开始调整，就可以让整棵树都满足大根堆的性质。那我们就可以从最后一个非叶子结点（因为叶子结点本身就是一个堆）开始调整，自底向上，从右往左地把一棵树构建成一个大根堆。像这样：

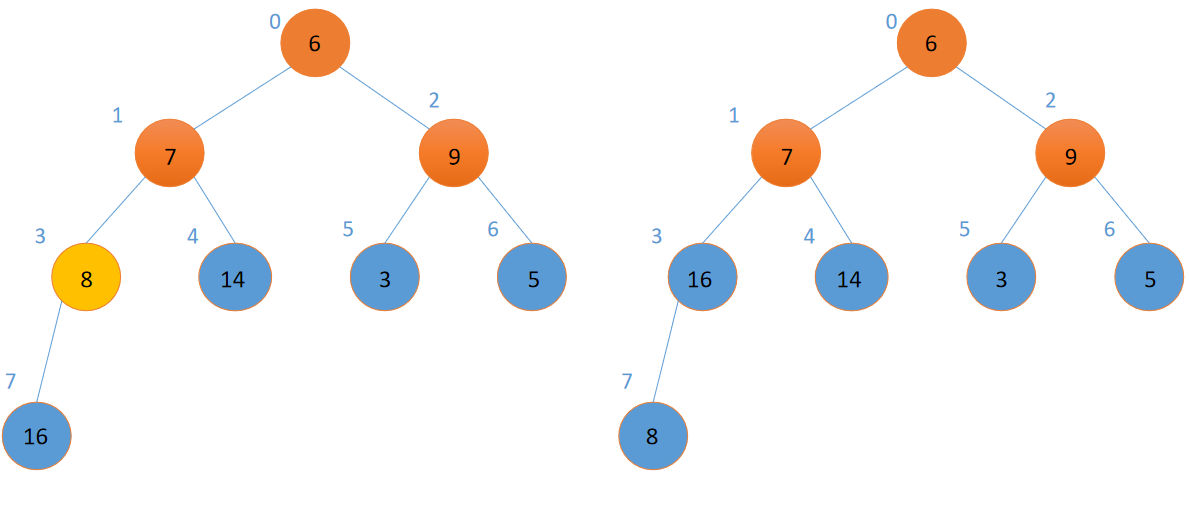
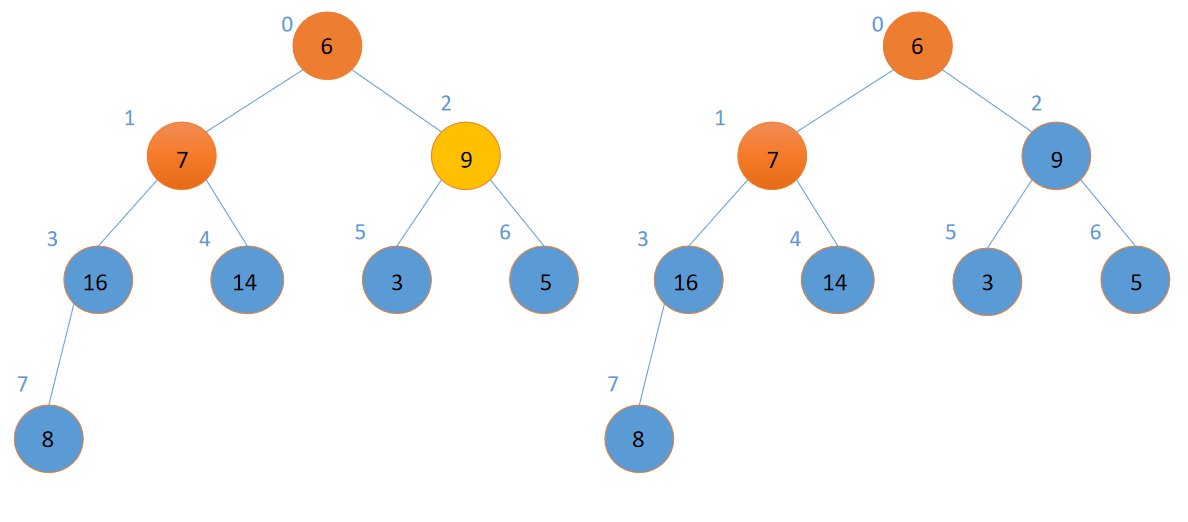
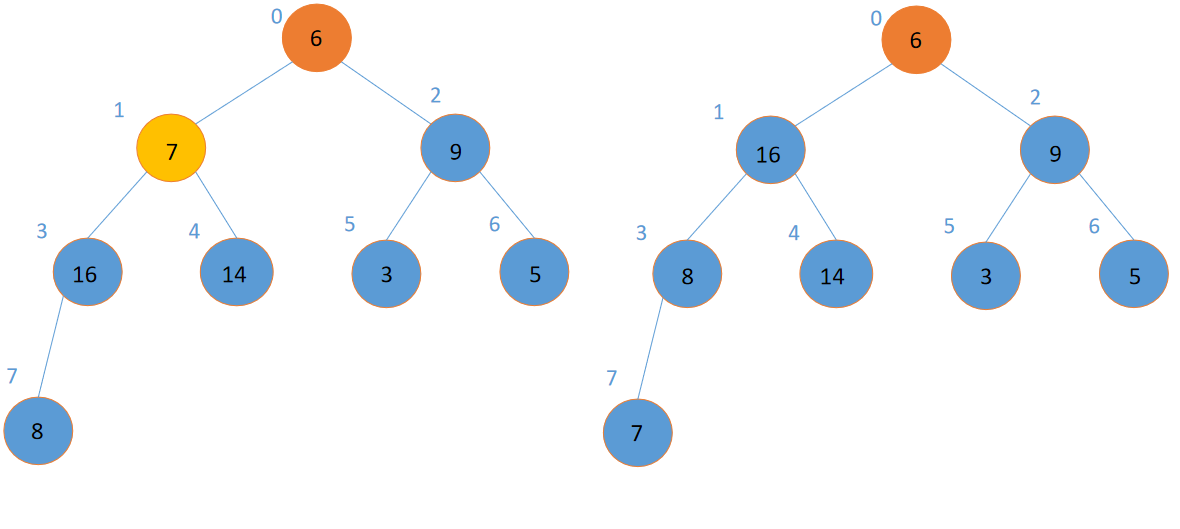
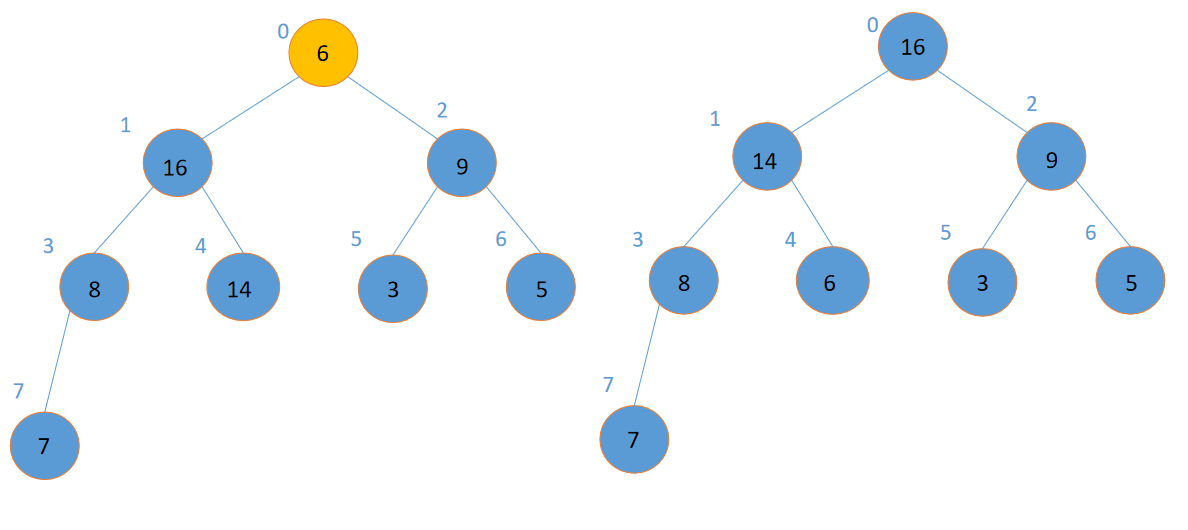
至此，一个大根堆就建成了！

把这个过程写成函数就是：

//建立大根堆
void build_max_heap(int *A, int size) {
	for (int i = (size - 1) / 2; i >= 0; i--) {
		max_heapify(A, i, size);
	}
}

堆排序

对一批无规则的数据，我们要先对他进行建堆的操作。

然后，我们可以每次都取大根堆堆顶的元素出来，把它和最后一个元素交换，然后调整堆。一直重复这样的操作，就可以把进行排序操作。

这个排序的过程像这样。

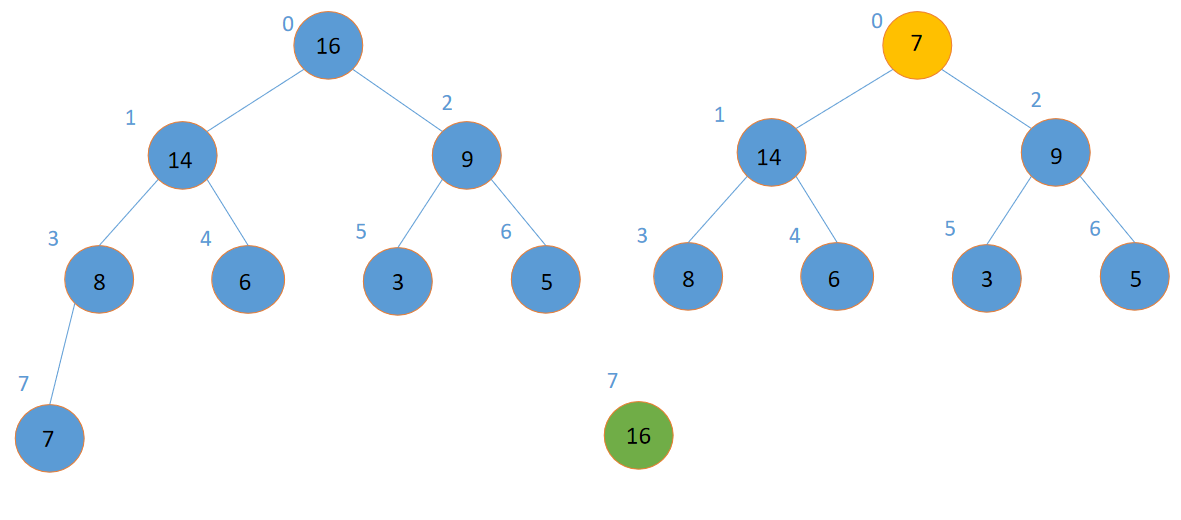
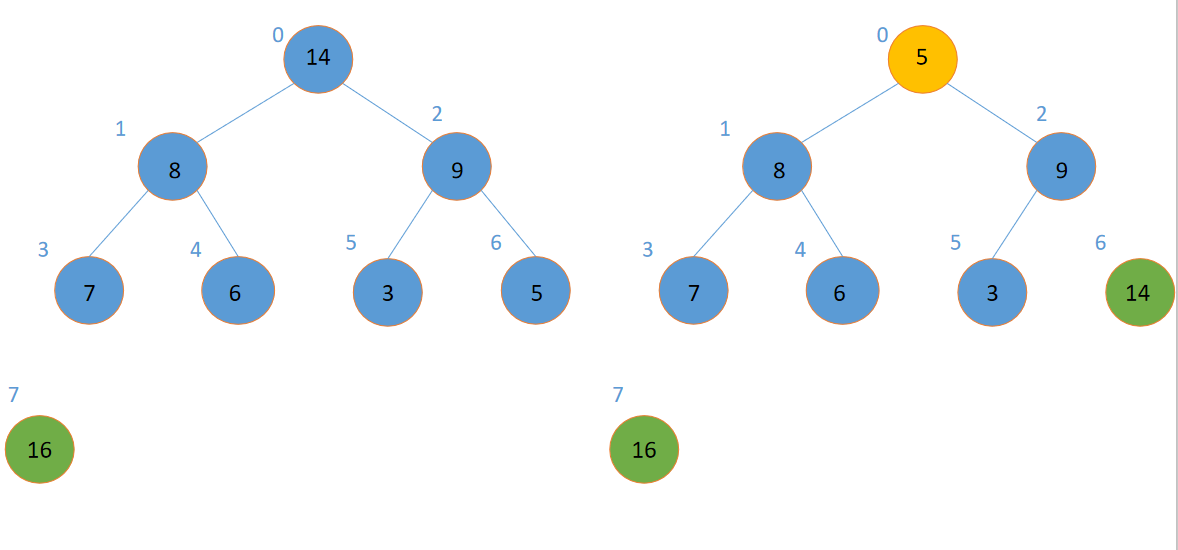
重复以上操作，我们就可以得到一个排好序的数组

这个过程写成函数：

void heap_sort(int *A, int size) {
	build_max_heap(A, size); //先建堆
	for (int i = size - 1; i > 0; i--) {
		swap(A[0], A[i]);   //交换堆顶和堆尾的元素
		max_heapify(A, 0, i);  //调整堆
	}
}

全部代码

#include<iostream>
#include<cstdlib>
#include<ctime>
using namespace std;

void swap(int &a, int &b) {
	int t = a;
	a = b;
	b = t;
}

//维护最大堆的性质
void max_heapify(int *A, int i, int size) {
	int L = i * 2 + 1;  //左孩子下标(默认下标从0开始）
	int R = i * 2 + 2; //右孩子下标
	int largest = i;   //记住i和i的左右孩子三者中最大的那个的下标
	if (L < size && A[L] > A[largest]) {
		largest = L;
	}
	if (R < size && A[R] > A[largest]) {
		largest = R;
	}
	//如果违背了最大堆的性质，则交换
	if (largest != i) {
		swap(A[largest], A[i]);
		//递归进行调整
		max_heapify(A, largest, size);
	}
}

//建立大顶堆
void build_max_heap(int *A, int size) {
	for (int i = (size - 1) / 2; i >= 0; i--) {
		max_heapify(A, i, size);
	}
}

void heap_sort(int *A, int size) {
	build_max_heap(A, size); //先建堆
	for (int i = size - 1; i > 0; i--) {
		swap(A[0], A[i]);   //交换堆顶和堆尾的元素
		max_heapify(A, 0, i);  //调整堆
	}
}


int main() {
	srand(time(NULL));
	int a[10];
	for (int i = 0; i < 10; i++) {
		a[i] = rand() % 10;
		cout << a[i] << " ";
	}
	cout << endl;
	heap_sort(a, 10);
	for (int i = 0; i < 10; i++) {
		cout << a[i] << " ";
	}
	cout << endl;
	system("pause");
}

参考资料：《算法导论》Thomas H. Cormen Charles E.Leiserson && Ronald L.Rivest Clifford Stein 著