编程除了使程序在所有可能的情况下都正确工作,还需要考虑程序的运行效率,上一节主要介绍了关于读写的优化,本节将对运算的优化进行分析。读写优化
编写高效程序需要做到以下两点:
- 选择一组合适的算法和数据结构
- 编写编译器能够有效优化以转换成高效可执行代码的源代码
第一点合适的算法和数据结构往往是大家写程序时会首先考虑到的,而第二点常被忽略。这里我们就代码优化而言,主要讨论如何编写能够被编译器有效优化的源代码,其中理解优化编译器的能力和局限性是很重要的。
除了读写与运算的区别,本节与上一节最大的不同的是:本次的优化示例会影响程序的可读性。
但这也是编程中时常会遇到的情况,在没有更好的优化手段,但又对程序有迫切的性能需求时,采取空间换时间,或降低代码可读性换取运行效率的方法并非不可取。
当你编写一个小工具临时处理某种事务(也许以后并不重用),或者想验证自己的某个想法是否可行时(比如测试某个算法是否正确),若是编写了一个可读性不错但运行很慢的程序,往往会浪费很多不必要的时间。这时候你就可以不需要那么在乎代码的可读性,而是去多关注当前程序的运行性能来更早获得想要的结果。
以下我们将举例对常见的矩阵运算进行代码优化。
目标函数:图像平滑处理
平滑操作要求:
- 修改图像矩阵的每个像素点的值,
新值 = 以该像素点为中心点所相邻的九个像素的平均值 - 图像矩阵的四个角点,只需要求角上四个像素的平均值
- 图像矩阵的四条边,只需要求当前点相邻的六个像素平均值
原理图:
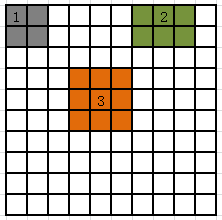
1、2、3处分别代表角点、边缘点以及内部点的相邻像素
我们用以下结构体表示一张图像的像素点:
typedef struct {
unsigned short red; /* R value */
unsigned short green; /* G value */
unsigned short blue; /* B value */
} pixel;
red、green、blue分别表示一张彩色图像的红绿蓝三个通道。
原平滑函数如下:
static void accumulate_sum(pixel_sum *sum, pixel p)
{
sum->red += (int) p.red;
sum->green += (int) p.green;
sum->blue += (int) p.blue;
sum->num++;
return;
}
static void assign_sum_to_pixel(pixel *current_pixel, pixel_sum sum)
{
current_pixel->red = (unsigned short) (sum.red/sum.num);
current_pixel->green = (unsigned short) (sum.green/sum.num);
current_pixel->blue = (unsigned short) (sum.blue/sum.num);
return;
}
static pixel avg(int dim, int i, int j, pixel *src)
{
int ii, jj;
pixel_sum sum;
pixel current_pixel;
initialize_pixel_sum(&sum);
for(ii = max(i-1, 0); ii <= min(i+1, dim-1); ii++)
for(jj = max(j-1, 0); jj <= min(j+1, dim-1); jj++)
accumulate_sum(&sum, src[RIDX(ii, jj, dim)]);
assign_sum_to_pixel(¤t_pixel, sum);
return current_pixel;
}
void naive_smooth(int dim, pixel *src, pixel *dst)
{
int i, j;
for (i = 0; i < dim; i++)
for (j = 0; j < dim; j++)
dst[RIDX(i, j, dim)] = avg(dim, i, j, src);
}
图像是标准的正方形,用一维数组表示,第(i,j)个像素表示为I[RIDX(i,j,n)],n为图像边长。
参数:
- dim:图像的边长
- src: 指向原始图像数组首地址
- dst: 指向目标图像数组首地址
优化目标:使平滑运算处理的更快
当前我们拥有一个driver.c文件,可以对原函数和我们优化的函数进行测试,得到表示程序运行性能的CPE(每元素周期数)参数。
我们的任务就是实现优化代码,与原有代码同时运行进行参数的对比,查看代码优化情况。
优化的主要方法
- 循环展开
- 并行计算
- 提前计算
- 分块运算
- 避免复杂运算
- 减少函数调用
- 提高Cache命中率
循环主体只存在一条语句,该语句主要是进行大量的均值运算,而且调用了多层的函数,这样运行时会出现多个函数栈的调用。
通过分析,本节的优化手段比上一节的矩阵读写要更直接。当前程序主要的性能瓶颈在于两个方面:
- 多层函数调用:增加了不必要的函数栈处理开销
- 大量重复运算:不同像素点在进行均值运算时,很多运算都是重复且不必要的
本节的优化就是针对这两点进行改进,
多层函数调用比较容易解决,只需要把被调用函数转移在平滑函数中实现就行(原代码降低了耦合度,但却导致了性能的下降)。
下面主要分析重复运算的问题,如图:
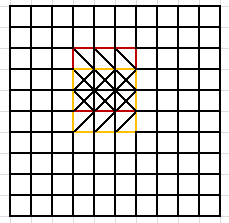
计算红色区域平均值与黄色区域平均值时,有两行是重复运算的。相应的优化策略是以1*3小矩阵为组计算和,这样每次计算均值只需要3个已知的和相加除以9,减少了一定的运算量。
相应的优化代码如下:
int rsum[4096][4096];
int gsum[4096][4096];
int bsum[4096][4096];
void smooth(int dim, pixel *src, pixel *dst)
{
int dim2 = dim * dim;
for(int i = 0; i < dim; i++){
for(int j = 0; j < dim-2; j++){
int z = i*dim;
rsum[i][j] = 0, gsum[i][j] = 0, bsum[i][j] = 0;
for(int k = j; k < j + 3; k++){
rsum[i][j] += src[z+k].red;
gsum[i][j] += src[z+k].green;
bsum[i][j] += src[z+k].blue;
}
}
}
// 四个角
dst[0].red = (src[0].red + src[1].red + src[dim].red + src[dim+1].red) / 4;
dst[0].green = (src[0].green + src[1].green + src[dim].green + src[dim+1].green) / 4;
dst[0].blue = (src[0].blue + src[1].blue + src[dim].blue + src[dim+1].blue) / 4;
dst[dim-1].red = (src[dim-2].red + src[dim-1].red + src[dim+dim-2].red + src[dim+dim-1].red) / 4;
dst[dim-1].green = (src[dim-2].green + src[dim-1].green + src[dim+dim-2].green + src[dim+dim-1].green) / 4;
dst[dim-1].blue = (src[dim-2].blue + src[dim-1].blue + src[dim+dim-2].blue + src[dim+dim-1].blue) / 4;
dst[dim2-dim].red = (src[dim2-dim-dim].red + src[dim2-dim-dim+1].red + src[dim2-dim].red + src[dim2-dim+1].red) / 4;
dst[dim2-dim].green = (src[dim2-dim-dim].green + src[dim2-dim-dim+1].green + src[dim2-dim].green + src[dim2-dim+1].green) / 4;
dst[dim2-dim].blue = (src[dim2-dim-dim].blue + src[dim2-dim-dim+1].blue + src[dim2-dim].blue + src[dim2-dim+1].blue) / 4;
dst[dim2-1].red = (src[dim2-dim-2].red + src[dim2-dim-1].red + src[dim2-2].red + src[dim2-1].red) / 4;
dst[dim2-1].green = (src[dim2-dim-2].green + src[dim2-dim-1].green + src[dim2-2].green + src[dim2-1].green) / 4;
dst[dim2-1].blue = (src[dim2-dim-2].blue + src[dim2-dim-1].blue + src[dim2-2].blue + src[dim2-1].blue) / 4;
// 四条边
for(int j = 1; j < dim-1; j++){
dst[j].red = (rsum[0][j-1]+rsum[1][j-1]) / 6;
dst[j].green = (gsum[0][j-1]+gsum[1][j-1]) / 6;
dst[j].blue = (bsum[0][j-1]+bsum[1][j-1]) / 6;
}
for(int i = 1; i < dim-1; i++){
int a = (i-1)*dim, b = (i-1)*dim+1, c = i*dim, d = i*dim+1, e = (i+1)*dim, f = (i+1)*dim+1;
dst[c].red = (src[a].red + src[b].red + src[c].red + src[d].red + src[e].red + src[f].red) / 6;
dst[c].green = (src[a].green + src[b].green + src[c].green + src[d].green + src[e].green + src[f].green) / 6;
dst[c].blue = (src[a].blue + src[b].blue + src[c].blue + src[d].blue + src[e].blue + src[f].blue) / 6;
}
for(int i = 1; i < dim-1; i++){
int a = i*dim-2, b = i*dim-1, c = (i+1)*dim-2, d = (i+1)*dim-1, e = (i+2)*dim-2, f = (i+2)*dim-1;
dst[d].red = (src[a].red + src[b].red + src[c].red + src[d].red + src[e].red + src[f].red) / 6;
dst[d].green = (src[a].green + src[b].green + src[c].green + src[d].green + src[e].green + src[f].green) / 6;
dst[d].blue = (src[a].blue + src[b].blue + src[c].blue + src[d].blue + src[e].blue + src[f].blue) / 6;
}
for(int j = 1; j < dim-1; j++){
dst[dim2-dim+j].red = (rsum[dim-1][j-1]+rsum[dim-2][j-1]) / 6;
dst[dim2-dim+j].green = (gsum[dim-1][j-1]+gsum[dim-2][j-1]) / 6;
dst[dim2-dim+j].blue = (bsum[dim-1][j-1]+bsum[dim-2][j-1]) / 6;
}
// 中间部分
for(int i = 1; i < dim-1; i++){
int k = i*dim;
for(int j = 1; j < dim-1; j++){
dst[k+j].red = (rsum[i-1][j-1]+rsum[i][j-1]+rsum[i+1][j-1]) / 9;
dst[k+j].green = (gsum[i-1][j-1]+gsum[i][j-1]+gsum[i+1][j-1]) / 9;
dst[k+j].blue = (bsum[i-1][j-1]+bsum[i][j-1]+bsum[i+1][j-1]) / 9;
}
}
}
运行效率如下:
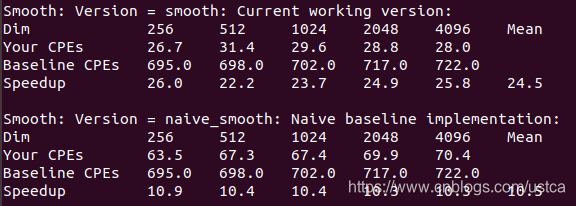
- Dim:图像大小
- Your CPEs:对应函数CPE
- Baseline CPEs:参考基线CPE
- Speedup:加速比 = Baseline CPEs / Your CPEs
原函数加速比为10.5,优化后加速比提升到24.5,虽然一定程度上损失了些代码的可读性,但提升了我们想要的运行效率。
优化在一定程度上减少了重复的运算,但并没有完全消除重复运算,如果有更好的优化方法欢迎交流。