普通树与二叉树

树

树作为一种常用的数据结构，不可不知。树采用的是链式存储，在详细介绍树之前要先了解几个基本概念：

根、节点、孩子、双亲、兄弟、分支 就不多BB了，叶子指的是没有子节点的节点，树的高度指从根到树所有叶子节点的最大长度，节点的度为其子节点的数量，节点的深度为节点到根的路径长度。

二叉树

二叉表示至多两向选择，在许多场景下都有应用。二叉树的种类实在太多，今天先宽泛地说一下几种二叉树。

严格二叉树

严格二叉树是这样的二叉树，它的每个节点或者没有孩子或者有两个孩子，即没有一个孩子的节点。

满二叉树

满二叉树要求每一层的节点数量都达到最大。

完全二叉树

在一棵完全二叉树中，除最后一层之外，每一层都有在这一层上可能的最大节点数量。最后一层的节点数量可以小于最大可能数量，但是它们必须是从左到右一个一个挨着排列的。

（实在太简单，就不上图了）

二叉树的遍历与署名

二叉树的遍历

可以大致分为前序遍历、中序遍历、后序遍历与层级遍历，前三种的区别只在于访问根节点相对左右子节点的访问顺序，层级遍历则是按照层级，一层一层逐级遍历节点。很明显，前中后序三中遍历用递归实现非常简单，有兴趣用循环实现的同学可以参考我另一篇博客递归转循环的通法。不好意思，盗个图先，嘻嘻。

二叉树的署名

数据结构的署名是这一结构及其内容的纯文本形式的编码，这一署名可以离线存储，并在需要时在内存中重构该数据结构。（说白了，持久化存储）

既然要持久化二叉树，那么其存储结构必须要唯一标识二叉树，不能产生歧义，否则存储的结构无意义。层级遍历结果首先否定，因为其完全无法提供节点层级与节点的父子关系。再来看三序遍历，单单一种遍历同样无法区分，那么两种遍历结合到一起呢？

假设所有节点存储的数据内容不同，在此前提下，前后序遍历无法唯一标识，因为无法提供节点之间的父子关系。而前中与中后则可以，有兴趣的同学可以思考一下，不深入讨论了。

这里给出鄙人实现的二叉树JAVA代码，请轻拍。

package com.structures.tree;

/**
 * Created by wx on 2017/11/2.
 * BinaryTree Node class.
 */
public class BinaryTree<T> {
    private T data;
    public BinaryTree<T> left;
    public BinaryTree<T> right;
    public BinaryTree<T> parent;

    // 子类无法继承父类的构造方法，需要的话，就显示调用;T申明过了，除了static不用再申明
    public BinaryTree(){
        T data = null;
        BinaryTree<T> left = null;
        BinaryTree<T> right = null;
        BinaryTree<T> parent = null;
    }

    // 初始节点值
    public void makeRoot(T data){
        if(this.data!=null)
            throw new TreeViolationException("The tree is not null!");
        else
            this.data = data;
    }

    //设定节点值
    public void setData(T data){
        this.data = data;
    }

    public T getData(){
        return data;
    }

    // 返回整棵树的根
    public BinaryTree<T> root(){
        BinaryTree<T> myRoot = this;
        while(myRoot.parent!=null){
            myRoot = myRoot.parent;
        }
        return myRoot;
    }

    //设定左子树
    public void attachLeft(BinaryTree<T> tree){
        if(left!=null)
            throw new TreeViolationException("Left sub tree already exists!");
        left = tree;
        tree.parent = this;
    }

    //设定右子树
    public void attachRight(BinaryTree<T> tree){
        if(right!=null)
            throw new TreeViolationException("Right sub tree already exists!");
        right = tree;
        tree.parent = this;
    }

    //删除左子树并返回之
    public BinaryTree<T> detachLeft(){
        BinaryTree<T> subTree = left;
        subTree.parent = null;
        left = null;

        return subTree;
    }

    //删除右子树并返回之
    public BinaryTree<T> detachRight(){
        BinaryTree<T> subTree = right;
        subTree.parent = null;
        right = null;

        return subTree;
    }

    //返回是否为空树
    public boolean isEmpty(){
        return (data==null && left==null && right==null);
    }

    //清空二叉树，并使之与双亲节点断开
    public void clear(){
        if(parent!=null){
            if(parent.left==this)
                parent.left = null;
            else
                parent.right = null;
        }
        parent = left = right = null;
        data = null;
    }
}

class TreeViolationException extends RuntimeException{
    TreeViolationException(String info){
        super(info);
    }
}

普通树

普通树主要是以层次的形式组织起来的，最常见的就是Unix操作系统的文件组成层次，生活中又如企业的管理层级。话不多说，上图。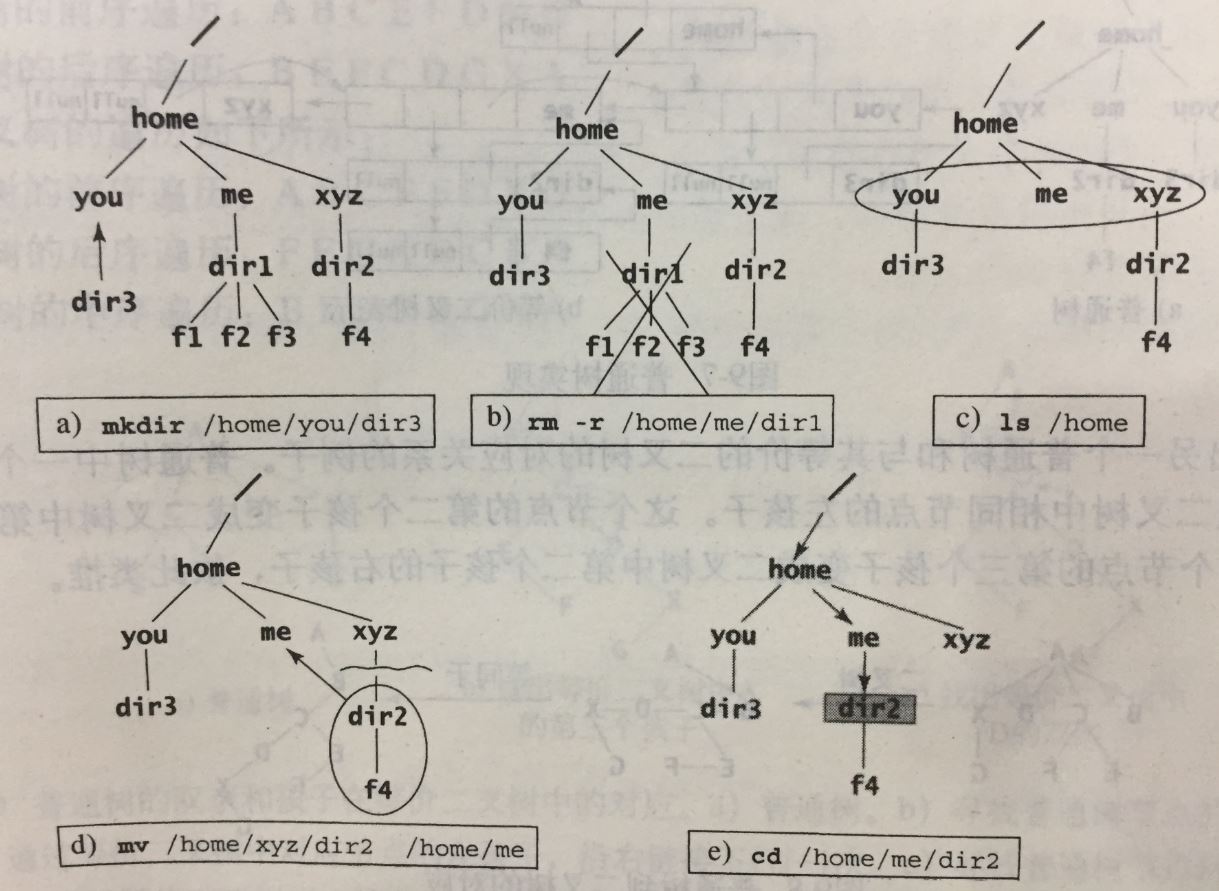

树的理解和构建都很简单，但是相对二叉树又有很多一些问题。

问题一：存储空间问题

普通树的节点的孩子数量是不确定的，那么直接构建足够引用孩子节点空间的节点是行不通的。在不知道一个节点有多少个孩子的情况下，我们对节点要进行过高评估并分配一个最大空间，这会带来严重的空间浪费。假设节点的孩子最多k个，这棵树有n个节点，这个时候浪费的空间比例为：w = (nk-(n-1)) / (nk) ≈ 1- 1/k 。k=5时，几乎有80%的浪费！

问题二：普通树的署名

二叉树可以通过前中或者中后序遍历署名，那么普通树呢？ 首先普通树就不存在所谓的中序遍历，而前后序结合又不能唯一标识一棵普通树。然后，尴尬了！

怎么解决？

普通树实际上是以二叉树的形式存储，这样的话，上面两个问题就迎刃而解了。其与之对应的二叉树之间的转化关系为：

1. 对于普通树的节点A，A的第一个孩子变为二叉树中A的左孩子
2. A的右兄弟变为二叉树中A的右孩子,以此类推

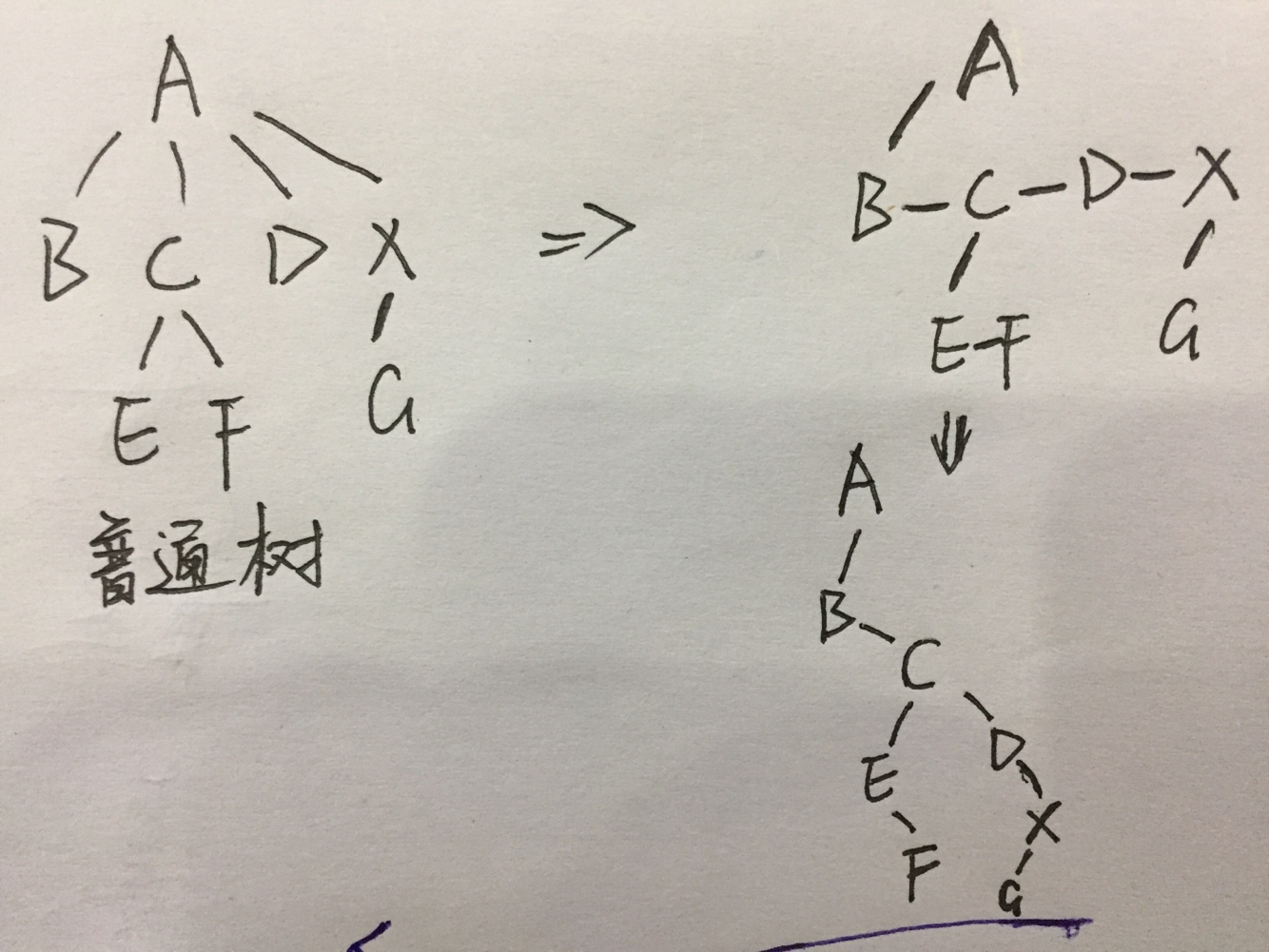
以图中树为实例，不妨写一下其遍历结果。

原来树的遍历：

• 前序遍历：ABCEFDXG
• 后序遍历：BEFCDGXA

转换后二叉树的遍历：

• 前序遍历：ABCEFDXG
• 中序遍历：FEGXDCBA
• 后序遍历：BEFCDGXA

呦，怎么普通树的前序遍历和后序遍历分别与等价二叉树的前序遍历和中序遍历结果相同啊？！

仔细分析一下，等价二叉树节点left 对应 原来子节点， 等价二叉树节点right 对应原来的 右兄弟， 等价二叉树的中序遍历的遍历顺序与原来的前序相同！

同理 等价二叉树的中序遍历 与 原来的后续遍历的遍历顺序相同。追根究底，就是这样对应转换，没有改变遍历节点的顺序规则。

普通树与等价二叉树一一对应，同时使用二叉树的署名也唯一标识了普通树，问题二解决！