引文
hello,今天写的数据结构是散列表(hash表),也算是一种基础数据结构了吧。学过计算机的人大概都能说出来这是个以空间换时间的东西,那么具体怎么实现的是今天要讨论的问题。
为什么需要它?主要还是人们希望能完成O(1)时间复杂度的查询,之前我们学习的最优秀的数据结构AVL树也是O(lg n)量级的。很多人想到了数组这种数据结构,数组可以随机访问,在知道索引的情况下,可以O(1)时间访问之。最初的思想是将关键字的值作为索引,在对应的位置上存储数字,以1、3、5、8为例,建立一个8个长度的数组,索引为1、3、5、8的位置存储true,其他为false,算是初步达到了目的。当然,后续的改进都是在此基础上进行的,基本思想没有变化。
如果只存两个数,1和10000,那岂不是要创建个10000长度的数组,但是只存两个有效数据吗?
那如果关键字是string呢?
这时候就需要一个函数,完成对关键字的转换工作,也即将原先的关键字转化为索引,根据索引存储数据。
定义
|
散列与散列函数 散列表是存储数组。散列是通过推演出对象的数值散列码,并把这个散列码映射到散列表中的位置来在散列表中存储对象的过程。将对象映射到散列表中位置的函数就叫散列函数。 |
散列冲突
有个问题必须要考虑,通过散列函数转化关键字,两个不同的关键字会不会转换结果相同?
当然会!存储数组位置是有限的,而输入变量在输入空间中是个无限可能的量,必然存在转换结果相同的情况,这种情况我们叫做散列冲突。有问题就要解决,如何解决冲突,可以先思考一下。哈哈,鄙人第一次考虑的时候猜对过其中一类办法,当然,不难。
说散列冲突之前,先说散列函数。有哪些散列函数?散列之前先将输入变量转换成整数,举个例子,先将字符串各个位置的字母编号加一起得到结果:
|
cat = 3+1+20 = 24 dog = 4+15+7 = 26 ear = 5+1+18 = 24 |
以上计算结果叫做散列码,知道散列码还不够,要将其映射到数组对应的位置上。比方说,数组大小为10。使用散列函数 h(k) = k mod 10,则以上三个单词有两个存储在4位置,发生了冲突。当然,你可以设计其他映射函数,但是肯定会有冲突的情况发生,如何解决散列冲突是最关键的。
开放寻址法
开放寻址法,在散列表内寻找另一个位置存储数据。常用的有线性探查法和二次探查法。
线性探查法设映射函数为h,表的规模为N,被映射的关键字是k。如果在表中散列位置h(k)上发生冲突,那么线性探查法依次检查位置(h(k) + i)mod N, i=1,2,...,直到某个(h(k) + i)是空位置,或者(h(k) + i)mod N = h(k)结束。 |
线性探查法有个问题,考虑最坏情况,所有存储值都在同一个位置冲突。每次寻找一个新的位置存储数据,第一次冲突寻找1次,第二次冲突2次,直到第N-1次冲突,需要寻找N-1次。
假设你的散列函数可以使得在表的各位置均匀地分布关键字。如上例中,10长度的数组中已经插入cat于第四个索引处。之后再插入一个数,各个位置的概率?发现除了4,和5之外位置为1/10,而5位置的概率为2/10。随着冲突项继续插入,这个概率会越来越大。
这种堆积效应使得插入和查找的复杂度都变为O(N)。
|
设散列函数为h,表的规模为N,要散列的关键字为k。那么,如果在散列位置h(k)发生冲突,二次探查法依次检查位置(h(k) +i2),直到某个位置是个空位置,或者已经检查过的位置。 |
相对线性探查法,二次探查确实可以一定程度避免堆积。但二次探查法最坏情况下,即所有关键字在同一个位置冲突下,数组的利用率为1/2。可以证明,对于任意素数N,一旦一个位置被检查两次,那么之后的所有位置都是被已检查过的位置。
//设在i和j结束于相同位置
(h+i2) mod N = (h+j2) mod N
→ (i+j)(i-j) mod N = 0
//因为N是素数,它必须整除因子(i+j)或(i-j),只有做了N次探查,N才能整除(i-j);同时,使得N整除(i+j)的最小(i+j)为N。
→ i+j = N → j = N - i
//故而不同的探查位置数只能是N/2。
最坏情况的搜索和插入运行时间依旧是O(N)。
封闭寻址法
封闭寻址法不把关键字存储在表中,而是把散列在相同位置的所有关键字都存储在一个“吊挂”在那个位置上的数据结构中。最常见的就是链表,在java中java.util.HashMap就采用这样的设计。盗图盗图:
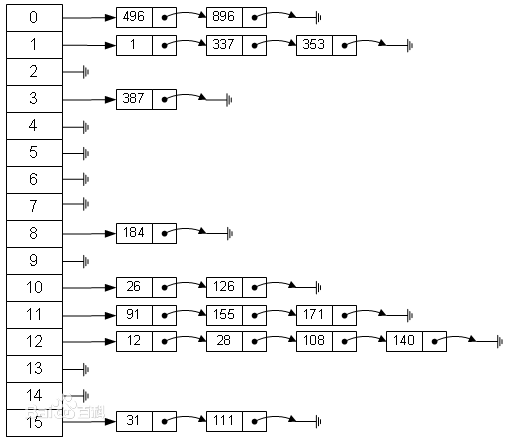
先介绍一个量,负载因子 a = n/N,n为散列表中的实际项数,N为散列表的容量。一般来说,负载因子越大,搜索的时间就越长。
同开放寻址法,最坏的插入和搜索的时间复杂度都是O(n),当然如果是对关键字完美散列的散列函数,时间复杂度都是O(1)。
java中HashMap是一种字典结构,实现了散列表的功能,存储(key,value)键值对,至少支持get(key)、put(key,value)、delete(key)方法。广义上来说,列表和二叉查找树都是字典。
HashMap的创建
// 创建默认容量为16,默认负载因子上限为0.75的hashmap HashMap<String,String> phoneBook = new HashMap<String,String>(); // 创建默认容量大于101的hashmap,但hashmap容量为2的幂,故实际容量为128 HashMap<String,String> phoneBook = new HashMap<String,String>(101); // 创建初始容量为128,负载因子上限为2.5的散列表 HashMap<String,String> phoneBook = new HashMap<String,String>(128, 2.5);
实际负载因为 a = n/N , 此处设置的上限,超过负载因子上限的时候,就会进行散列表扩展,每次扩展都为之前的2倍。
HashMap项的存储
以鄙人的1.8版本jdk为例,其成员变量:
/* ---------------- Fields -------------- */ transient Node<K,V>[] table; transient Set<Map.Entry<K,V>> entrySet; transient int size; int threshold; final float loadFactor;
transient关键字声明的成员不能被序列化和反序列化,与本文关系不大,不用在意。
size是散列表的实际存储项数
threshold是散列表项数上限,等于容量和负载因子上限的乘积:N*t,因此size最大值为threshold。
loadFactor是初始化时设定的负载因子上限值。
Node<K,V>[] table 构建一个链表数组,每一个Node<K,v>都是一个节点,Node对用户不可见,其数据结构为:
static class Node<K,V> implements Map.Entry<K,V> { final int hash; final K key; V value; Node<K,V> next;
... }
HashMap操作
源码写到东西太多了,代码就用简化版本吧,声明一下,这个不是jdk1.8源码啊,可能是老版本的。
添加项
1 public V put(K key, V value) { 2 K k = mashNull(key); 3 int hash = hash(k); 4 int i = indexFor(hash, table.length); 5 6 for(Node<K,V> e = table[i]; e!=null; e=e.next){ 7 if ((e.hash == hash)&&(eq(k, key)){ // eq判断是否相等 8 V oldValue = e.value; 9 e.value = value; 10 e.recordAccess(this); 11 return oldValue; 12 } 13 } 14 ++modCount; 15 addNode(hash, k, value, i); 16 return null; 17 }
Node的数据结构如下:
static class Node<K,V> implements Map.Entry<K,V> { final int hash; final K key; V value; Node<K,V> next; Node(int hash, K key, V value, Node<K,V> next) { this.hash = hash; this.key = key; this.value = value; this.next = next; } ... }
2行mashNull()处理为空的情况,indexFor将散列码映射到表位置上:
static int indexFor(int h, int length){ return h & (length-1); }
其作了一个位操作,按位并,length是2的幂,(length-1)与h并,就是取模,这个思考一下,很简单的。
addNode()为插入操作。
void addNode(int hash, K key, V value, int bucketIndex){ Node<K,V> e = table[bucketIndex]; table[bucketIndex] = new Node<K,V>(hash, key, value, e); if (size++ >= threshold) resize(2*table.length); }
在表中插入的位置称为桶,resize()是再散列方法,新表容量是原表的2倍。代码如下:
void resize(int newCapacity){ Node[] oldtable = table; int oldCapacity = oldtable.length; if(oldCapacity == MAXIMUM_CAPACITY){ threshould = Integer.MAX_VALUE; return; } Node[] newTable = new Node[newCapacity]; transfer(newTable); table = newTable; threshould = (int)(newCapacity*loadFactor); }
如果旧容量已经达到最大可能值而没有满足需要,那就将最大容量上限设为最大可能整数值,然后返回。如果不是的话,就创建2倍容量的新表,并对原表中的项重新散列。考虑下散列码1和9在容量8下索引都为1,但在16容量下索引分别为1和9,故需要重新散列。这个功能在方法transfer()中实现。
void transfer(Node[] newtable){ Node[] src = table; int newCapacity = newtable.length; for(int j=0; j<src.length; j++){ Node<K,V> e = src[j]; if(e!=null){ src[j] = null; do{ Node<K,V> next = e.next; int i = indexFor(e.hash, newCapacity); e.next = newtable[i]; newtable[i] = e; e = next; }while (e!=null); } } }
以上。