先说堆吧,把堆搞清楚了,堆排序自然不在话下。
堆
堆的定义:
|
堆是有如下性质的完全二叉树:任意节点x处的项的关键字大于或等于以x为根的子树中的所有节点处的项的关键字。 |
堆有两个性质:
- 结构性质——完全二叉树。
- 顺序性质——某节点处的关键字大于或等于(小于或等于)其子树节点的关键字。

要声明的是,堆这种数据结构,从根节点向下的路径是有序的,但是同一个根节点的左右孩子之间谁大谁小无所谓,也即不同路径的节点之间是没有必然的大小关系。
请读者思考,为什么堆要是完全二叉树?
如果顺序上是根大于等于子树节点,那就是大根堆,如果小于等于就是小根堆。本文以大根堆为例研究堆的性质。
堆有什么用呢?除了本节讨论的排序之外,堆还可以用来实现优先队列。
堆的操作
插入
可分为两步:
- 将待插入元素插入至最后一层最右边节点的右侧第一个位置(如果最后一层未满,满的话重新开一层)。
- 对插入节点向上调整位置。
举两个例子:

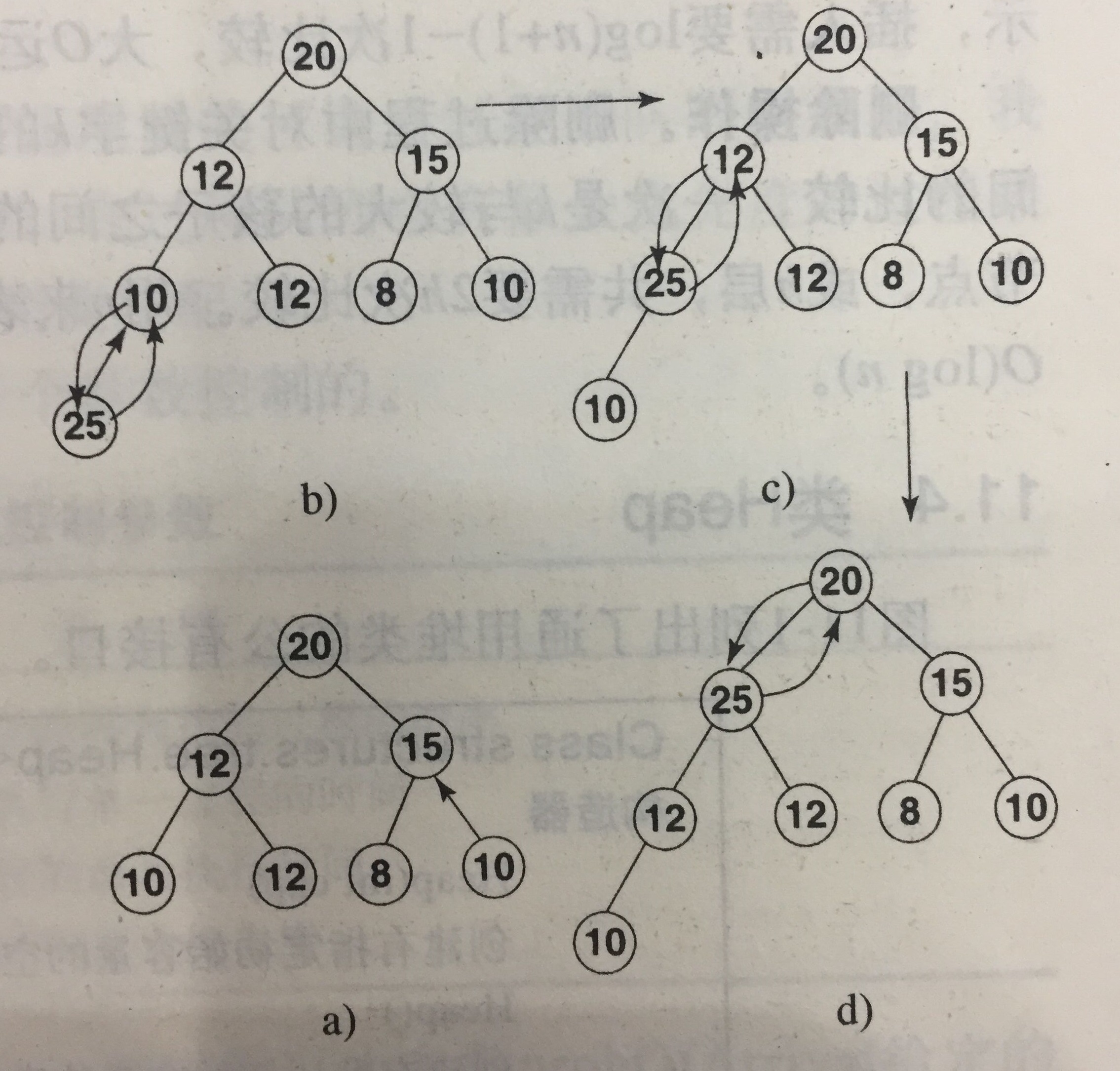
这里涉及到一个上移操作,也即将节点和双亲节点比较,如果比双亲大就交换位置,然后继续上行,否则停止上移。
为什么可以这样做,因为原来的树是满足堆的性质的,我们只需要调整插入节点的位置即可。
删除
删除堆顶元素,然后调整整个堆,使得其仍旧满足堆的性质。大致分为三步:
- 删除堆顶元素
- 将堆最后一个元素移动至堆顶
- 对堆顶向下调节位置。
看个实例图(有手机真好,不用动手画,嘿嘿):

这里涉及到一个下移操作,也即节点的左右孩子先作比较,确定较大的那个之后,再和节点比较,如果节点小于之,则交换位置并继续下行,否则停止下移操作。
同样的,除了堆顶外其余节点是堆有序的,只需调整新的堆顶元素即可。
操作时间复杂度
树高为 lg n, 所以上移和下移的路径最长为 lg n, 故而每次插入和删除操作的时间复杂度都是O(lg n)。
堆的物理结构
难道不是链表吗?天真!堆实际上是以数组为介质进行存储。堆的逻辑结构是完全二叉树,而物理结构是数组。为什么是这样?
之前我们问的问题还记得吗,堆为什么是完全二叉树?
- 一点可以想到的是,完全二叉树树高为 lg n,可以保证插入和删除操作的时间复杂度为 lg n 。
- 一点和它的物理结构数组有关,对索引 k 处的二叉树节点,其左右孩子的索引分别为(2k+1)和(2k+2),其双亲节点索引为(k-1)/2。已知索引就能对数组进行随机访问,等同于对其逻辑结构进行操作。
既然数组能同链表直接访问左右孩子和双亲,而且存储空间上又占优势,为什么不用数组呢?
大根堆实现
贴上鄙人的代码:
package com.structures.tree; /** * Created by wx on 2017/12/7. * Implement a max root heap. */ public class maxHeap<T extends Comparable<T>> { private Object[] heap; private int count; private int cursor; private static int DEFAULT_SIZE = 50; public maxHeap(int cap){ heap = new Object[cap]; count = 0; cursor = 0; } public maxHeap(){ heap = new Object[DEFAULT_SIZE]; count = 0; cursor = 0; } private int getParent(int index){ if(index<=0) throw new TreeViolationException("The node index is "+index+", has no parent node!"); return (index-1)/2; } private int getLeftChild(int index){ if(2*index+1>=heap.length) throw new TreeViolationException("The node index is "+index+", has no left child"); return 2*index+1; } private void exchange(int a, int b){ Object temp = heap[a]; heap[a] = heap[b]; heap[b] = temp; } public void add(Object item){ if(count>=heap.length-1) throw new TreeViolationException("The heap is fulled!"); else { heap[count] = item; if(count>1) siftUp(count); count++; } } private void siftUp(int index){ while(index>0){ int parentIndex = getParent(index); T a = (T)heap[index]; T b = (T)heap[parentIndex]; int compareResult = ((T)heap[index]).compareTo((T)heap[parentIndex]); if(compareResult>0) { exchange(index, parentIndex); index = parentIndex; } else break; } } public T deleteMax(){ if (isEmpty()) throw new TreeViolationException("The heap is empty!"); Object returnValue = heap[0]; heap[0] = heap[count-1]; heap[count-1] = null; count--; siftDown(0); return (T)returnValue; } private void siftDown(int index){ while(2*index + 1 < heap.length){ int leftIndex = getLeftChild(index); int maxIndex = leftIndex; if((leftIndex+1 < heap.length)&&(((T)heap[leftIndex+1]).compareTo((T)(heap[leftIndex]))>0)){ maxIndex = leftIndex+1; } if(((T)heap[index]).compareTo((T)(heap[maxIndex]))<0){ exchange(index, maxIndex); index = maxIndex; }else break; } } public void clear(){ heap = (T[]) new Object[heap.length]; } public int size(){ return count; } public boolean isEmpty(){ return count==0; } public T first(){ if(isEmpty()) throw new TreeViolationException("The heap is empty!"); cursor = 0; return (T)heap[cursor++]; } public T next(){ if(cursor>=count) throw new TreeViolationException("There is no element in next position!"); return (T)heap[cursor++]; } }
堆排序
好了,了解堆之后,如何利用堆实现排序功能?
依次插入构建堆
最初的想法是。一个一个插入元素,自动构建堆,然后每次删除堆顶元素,结果输出定为有序。
没问题! 那这样做的时间复杂度是多少?且看鄙人推导:

也就是说构建堆的时间复杂度是O(n lg n),删除堆的时间复杂度也为O(n lg n)。注意,在删除操作中,用最后一个元素替换堆顶元素的操作时间复杂度为O(1),此处忽略不计。所以总的时间复杂度为O(n lg n)。
有没有更好的办法?
有!原理是一样的,不过一次性输入整个待排序数组,也就是大家所了解的堆排序算法。其构建堆的时间复杂度为O(n),也即线性时间。
线性时间构建堆
这次是从数组元素原来位置开始调整结构,并不是从堆底向上调整,所以调整的路径长度就较短。
以何种方式构建?
在之前插入和删除元素时,我们分别上移和下移节点,那种做法的前提是其余部分已经有序,而此时情况有所不同,在调整一个节点的时候其余部分可能是无序的,所以不能完全套用原来的做法。
现在有两种思路,一种自顶向下,一种自底向上。
自顶向下
自顶向下怎么做?我想到了BFS算法,问题在于,一次调整后原位置的新节点可能需要再次调整,这种调整可能是无规律的,不知道什么时候能使得整棵树堆有序。难道一次一次迭代,直至收敛于满足堆性质处吗?好像不靠谱,或者说至少目前还没特别好的办法。
自顶向上
自底向上呢? 和DFS算法有点神似,算法思想是分治法。从堆底层开始,构建一个个小规模的堆,然后合并扩充,直至整棵树满足堆性质。
构建小规模堆的起始位置为堆内最右侧的第一个堆,以下图为例,是9,等同于对该节点进行下移操作。然后依次向左,每次操作都是堆从无到有、从小到大的过程。
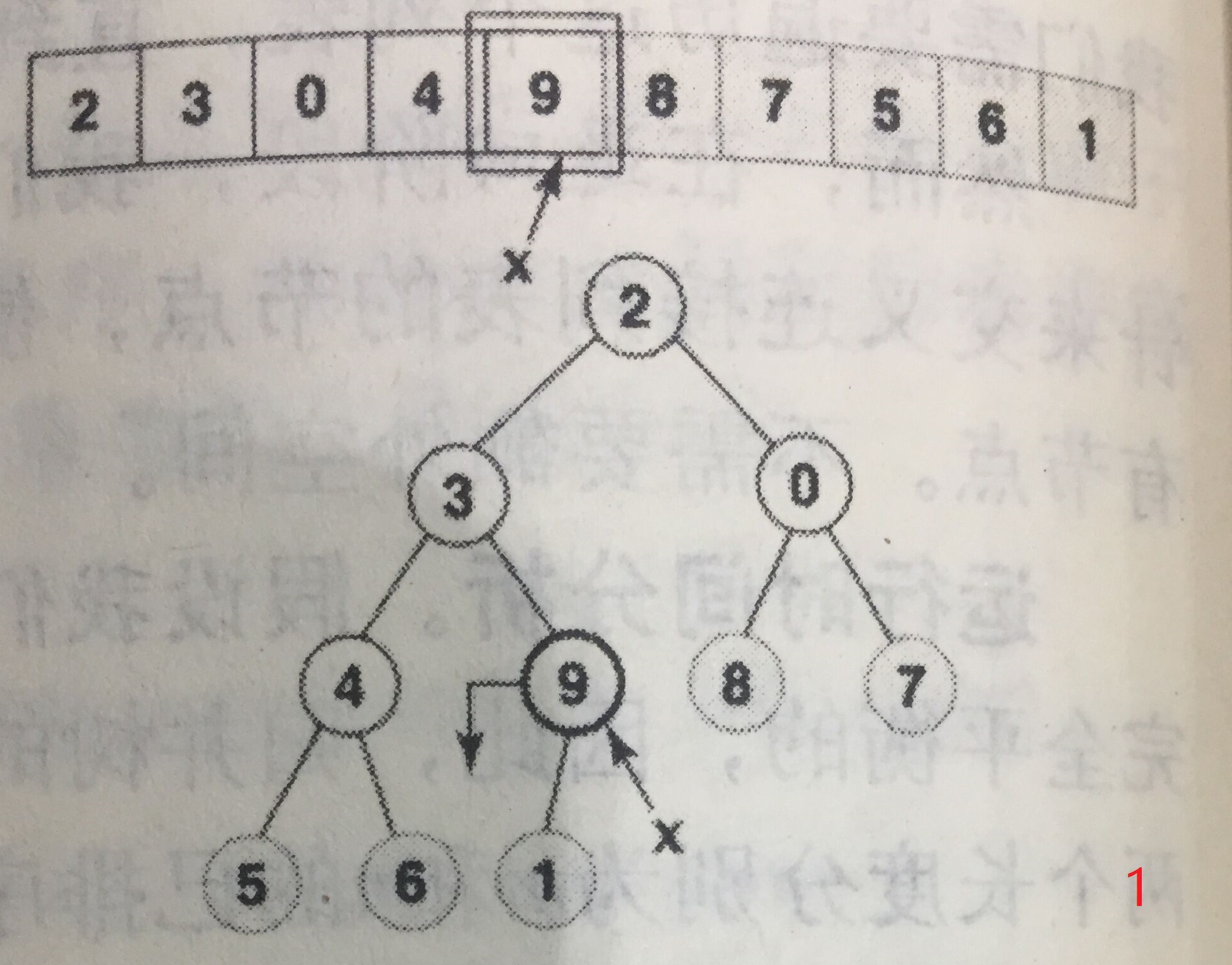
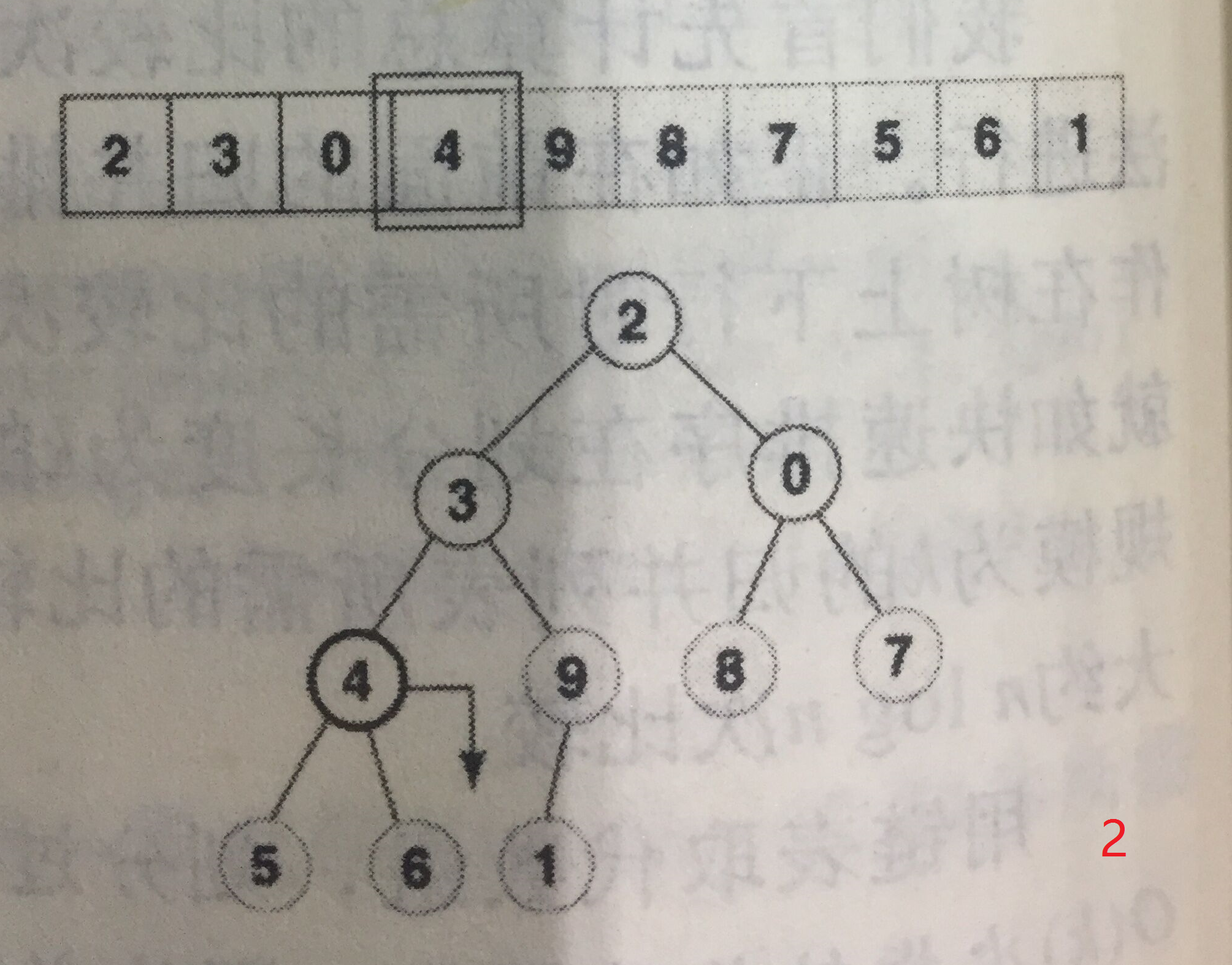
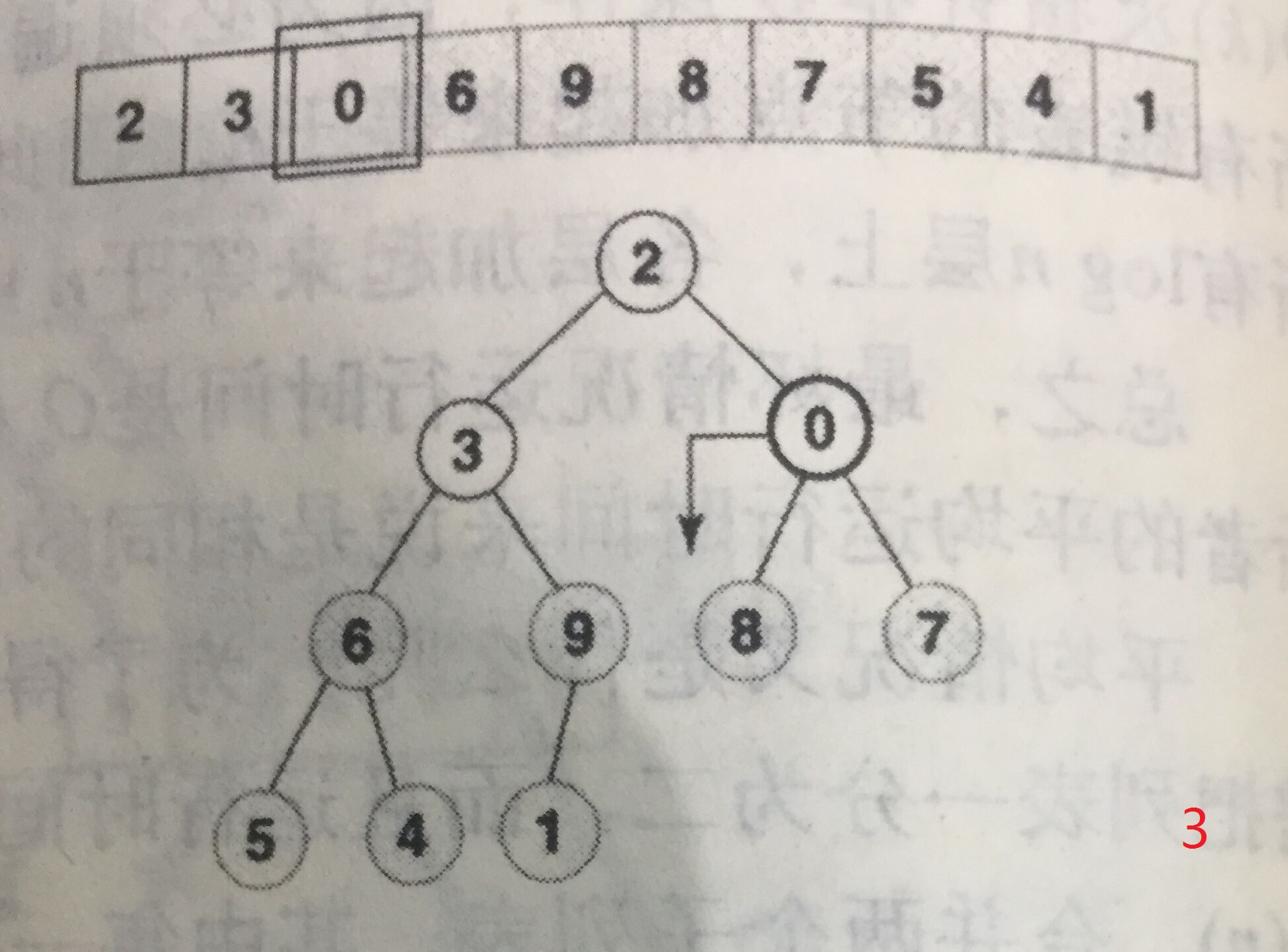
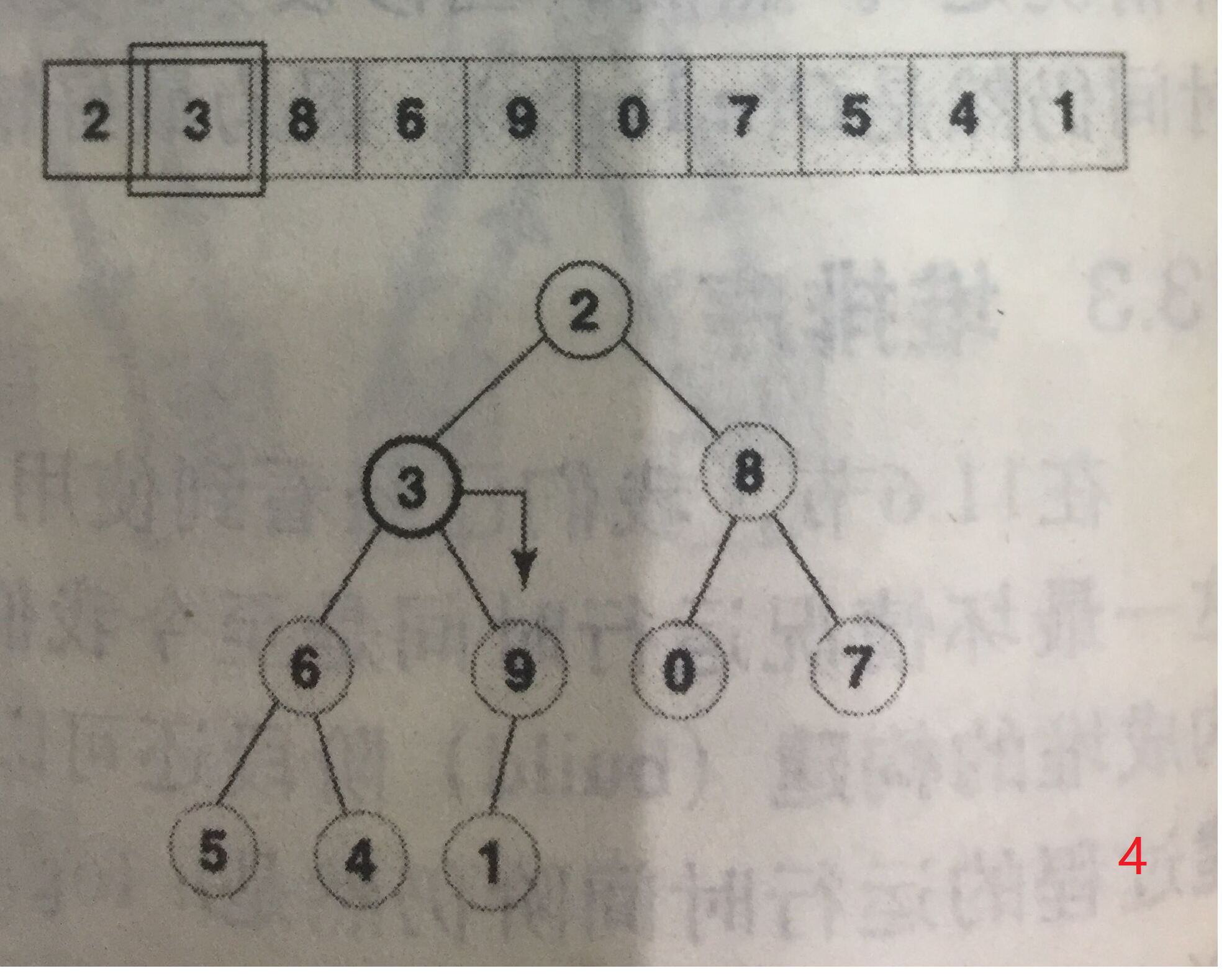
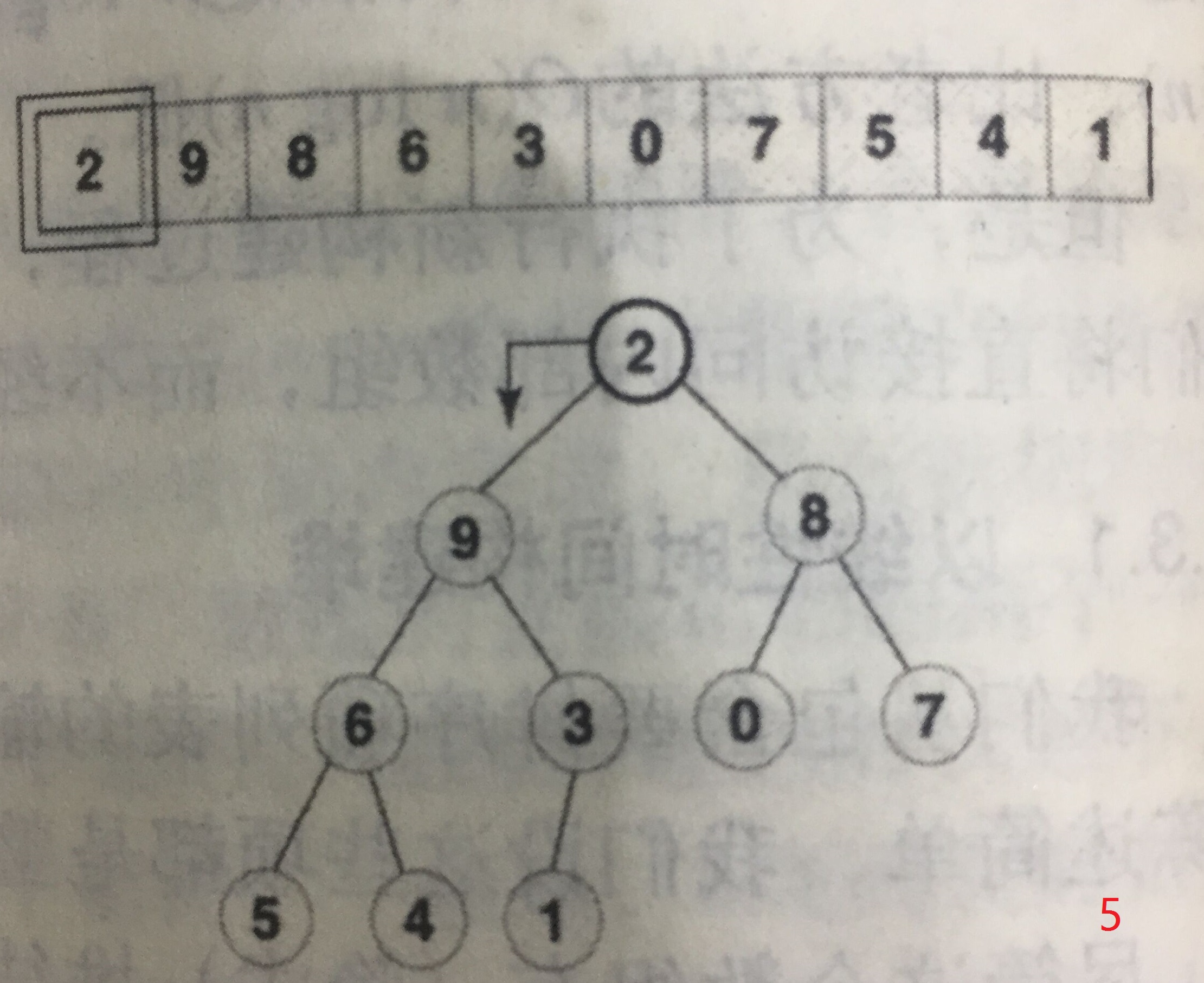
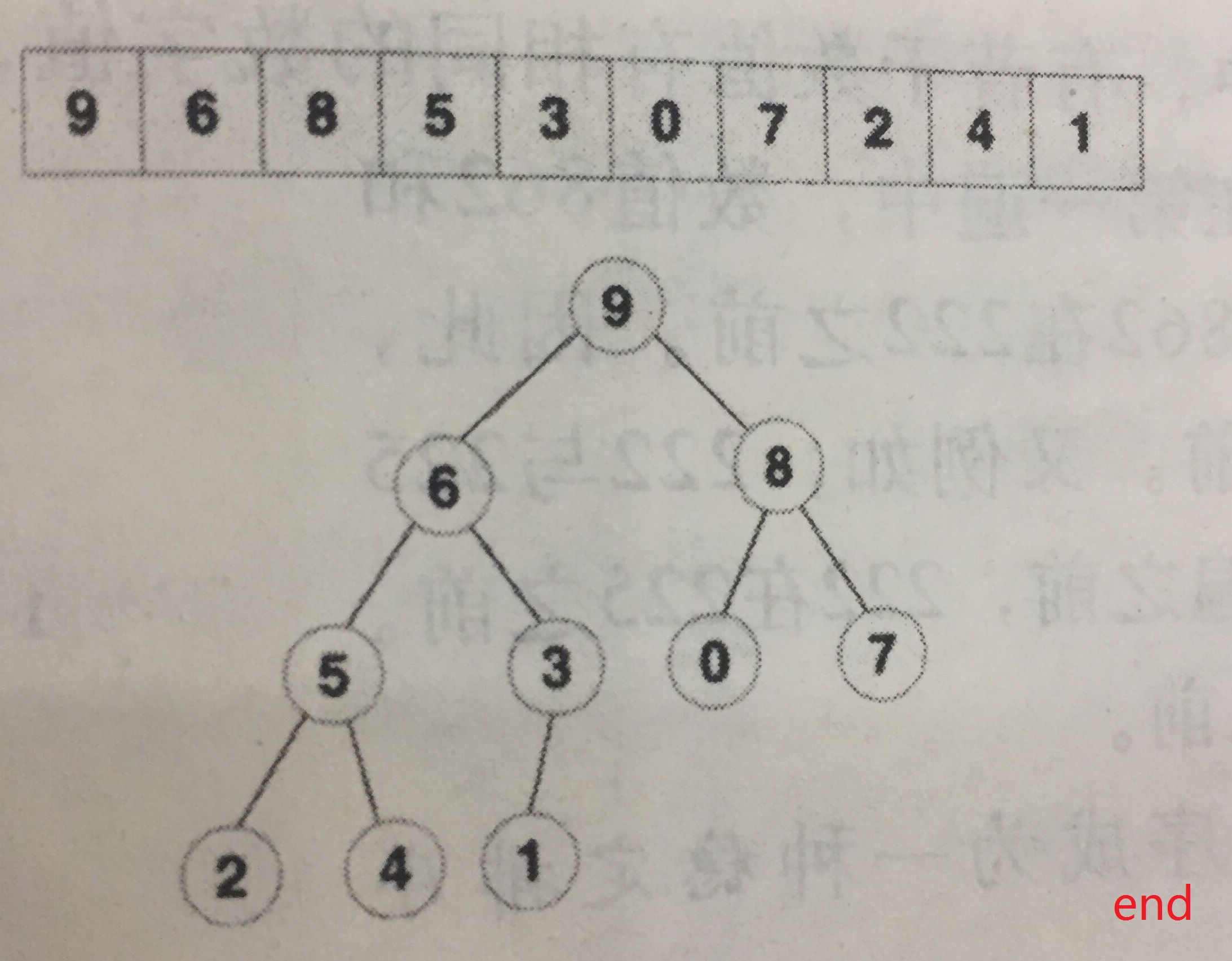
注意,每个节点下移的最大长度已经和之前依次插入时不同了,这样构建的时间复杂度见推导:
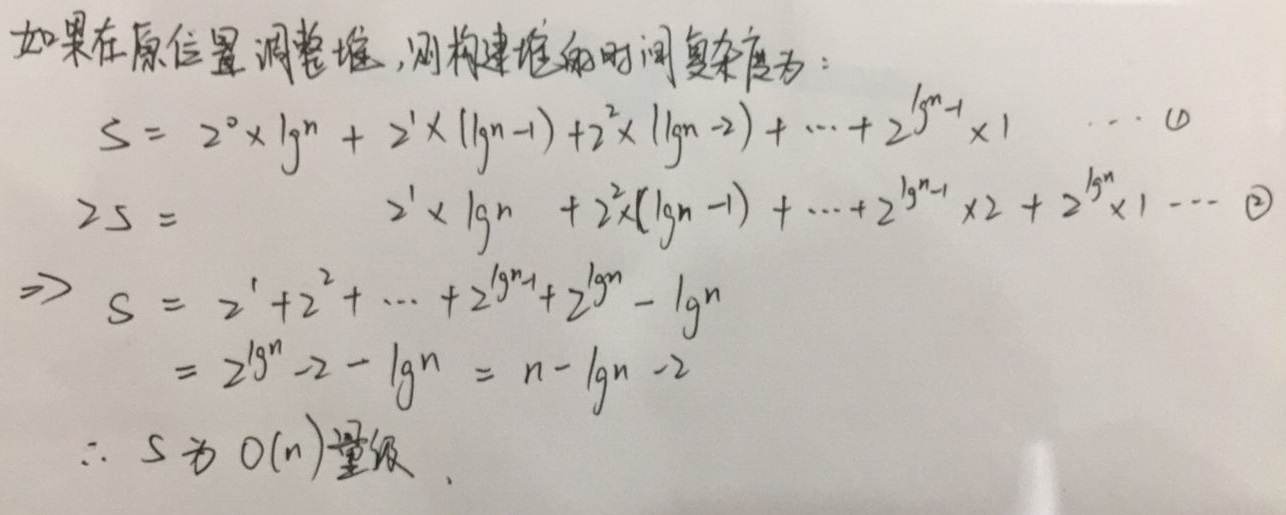
构建时间复杂度为O(n),比起一个一个插入O(n lg n)快。伪代码如下:
build_heap(A) n ← A.length; x ← (n-1)/2; while(x>=0) do v ← value at x; sift_down(v); x ← x-1; end while
输出过程同普通堆,删除堆顶元素,重新调整堆,时间复杂度为O(n lg n),所以总的时间复杂度为O(n lg n)。
堆排序实现
鄙人写了个小根堆的python版本堆排序算法,请指正:
1 class heap_sorter(object): 2 def __init__(self, data_list): 3 self.data_list = data_list 4 5 def sort(self): 6 self.build_heap() 7 self.travel() 8 9 def build_heap(self): 10 x = (len(self.data_list) - 1) / 2 11 12 while x >= 0: 13 self.sift_down(x) 14 x -= 1 15 16 def sift_down(self, index): 17 size = len(self.data_list) 18 19 while 2 * index + 1 < size: # 下行节点值 20 small_sub = 2 * index + 2 21 if (2 * index + 2 < size and self.data_list[2 * index + 2] < self.data_list[2 * index + 1]) 22 else 2 * index + 1 23 24 if self.data_list[index] > self.data_list[small_sub]: 25 temp = self.data_list[index] 26 self.data_list[index] = self.data_list[small_sub] 27 self.data_list[small_sub] = temp 28 else: 29 break 30 index = small_sub 31 32 def delete_heap(self): # 删除堆顶元素并返回 33 size = len(self.data_list) 34 35 while size > 0: 36 re_value = self.data_list[0] 37 self.data_list[0] = self.data_list[size-1] 38 self.data_list.pop() 39 self.sift_down(0) 40 size -= 1 41 42 yield re_value 43 44 # 对返回元素操作 45 def travel(self): 46 my_travel = self.delete_heap() 47 48 while len(self.data_list) > 0: 49 print my_travel.next()