哈希表

参考这篇博客，再加上自己的一些理解，总结了一下。

1. 概念

  哈希表也叫散列表，是一种查找算法，它尽量能不经过任何比较，通过一次存取就能得到所查找的数据元素。

因此需要存在一种映射关系，使每个关键字和哈希表中唯一一个存储位置相对应，这个映射关系叫做散列函数。

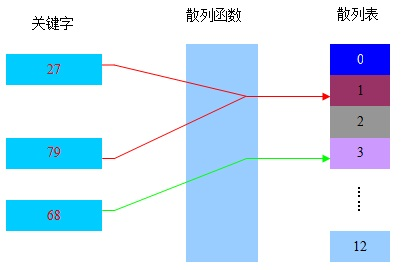
2. 常见的哈希函数

• 直接定址法

  取关键字或关键字的某个线性函数值为哈希函数，即：

    h(key) = key 或者 h(key) = a*key + b

• 数字分析法

  假设关键字是以r为基的数，并且哈希表中可能出现的关键字都是事先知道的，则可取关键字的若干数位组成哈希地址。

• 平方取中法：

  取关键字平方后的中间几位为哈希地址。通常在选定哈希函数时不一定能知道关键字的全部情况，取其中的哪几位也不一定合适，而一个数平方后的中间几位数和数的每一位都相关，由此使随机分布的关键字得到的哈希地址也是随机的。取的位数由表长决定。

• 折叠法

  将关键字分割成位数相同的几部分（最后一部分的位数可以不同），然后取这几部分的叠加和（舍去进位）作为哈希地址。

• 除留余数法

   取关键字被某个不大于散列表表长m的数p除后所得的余数为散列地址，即：

    h(key) = key MOD p ，其中p <= m

• 随机数法

  选择一个随机数，取关键字的随机函数值是它的哈希函数，即：

    h(key) = random(key)

3. 处理冲突

  讲道理，无论你的哈希函数设计得多巧妙，当关键数一多，必然会产生冲突，即两个关键字经过哈希函数后的值相同，这就需要一些冲突处理方式来解决。

• 开放地址法

  hi = (h(key) + di) MOD m， 其中i =1,2,…,k(k ≤ m-1)

其中的di又有三种取法：
  a. di = 1,2,3,…,m-1，称线性探测再散列
  b. di = 12,-12,22,-22,32,…,±k2 (k ≤m/2)，称二次探测再散列
  c. di = 伪随机数序列，称伪随机探测再散列

• 再散列法

  hi = rhi(key) i = 1,2,…,k
  rhi是指不同的散列函数

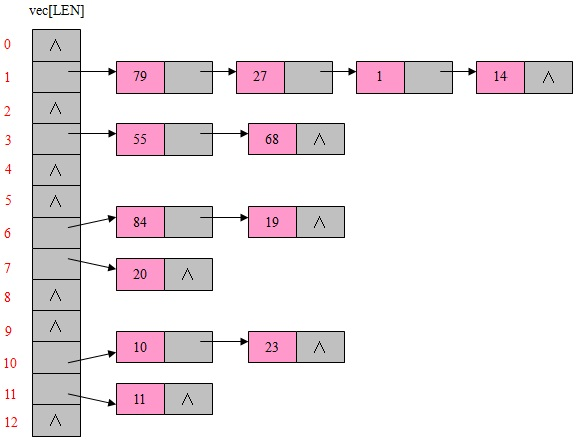
• 链地址法

  将所有关键字为同义词的数据元素存储在同一线性链表中。假设某散列函数产生的散列地址在区间[0,m-1]上，则设立一个指针型向量void *vec[m],其每个分量的初始状态都是空指针。凡散列地址为i的数据元素都插入到头指针为vec[i]的链表中。在链表中的插入位置可以在表头或表尾，也可以在表的中间，以保持同义词在同一线性链表中按关键字有序排列。

• 建立一个公共溢出区

4. 代码实现

    //例子以除留余数法和链地址法构造散列表
    #include <iostream>
    #include <fstream>
    using namespace std;
    #define LEN 13  
      
    struct hash_node {  
        int count;  
        struct hash_node *next;  
    };  
      
    int hash(int num)  
    {  
        return num % LEN;  
    }  
      
    void collision(struct hash_node *vec[], int elem, struct hash_node *new)  
    {  
        if (vec[elem] == NULL)  
            vec[elem] = new;  
        else  
        {  
            new -> next = vec[elem];  
            vec[elem] = new;  
        }  
    }  
      
      
    void create_hash(struct hash_node *vec[], int num)  
    {  
        ifstream in("data.in");  
        int i, tmp, arr[num];  
        struct hash_node *p;  
      
        for (i = 0; i < num; i++)  
            in >> arr[i];
            
        in.close();
      
        for (i = 0; i < num; i++) {  
            p = new hash_node;  
            p -> count = arr[i];  
            p -> next = NULL;  
      
            tmp = hash(arr[i]);  
            collision(vec, tmp, p);  
        }  
    }  
    
    
    
    //元素插入
    void insert_hash_node(struct hash_node *vec[], int data)  
    {  
        int tmp;  
        struct hash_node *p = new hash_node;  
        p -> count = data;  
        p -> next = NULL;  
      
        tmp = hash(data);  
        collision(vec, tmp, p);  
    }  
    
    //删除
    void delete_hash_node(struct hash_node *vec[], int data)  
    {  
        int elem;  
        struct hash_node *p, *tmp;  
      
        elem = hash(data);  
        if (vec[elem] == NULL) {  
            cout << "error";  
            return;
        }  
        else  
        {  
            tmp = vec[elem];  
            while (tmp -> count != data) {  
                if (tmp -> next == NULL) {  
                    cout << "error";  
                    return;
                }  
                p = tmp;  
                tmp = tmp -> next;  
            }  
            p -> next = tmp -> next;  
            delete tmp;
        }  
    }  
    
    
    //查找和前面类似，不赘述