深度优先搜索
设无向图G,其中的所有顶点都标记为“没访问过”。选择G中的一个顶点v作为搜索起点,将v标记为“访问过”。然后,递归地搜索与v相邻但没有访问过的顶点。当访问完从v能到达的所有顶点之后,如果G中还有没访问过的结点,则再选一个没访问过的顶点作为新的搜索起点。
算法如下:
// L[v] 表示关于顶点v的邻接表
DFSTraverse(G)
{
T = Φ ; /*边集为空*/
count = 1; /*计数器*/
for (all v in V)
mark v "new";
while(there exists a vertex v in V marked "new")
Search(v);
}
void Search(v)
{
dfn[v] = count; /*对v编号,编号可以放在结点属性中*/
count ++ ;
mark v "old";
for(each vertex w in L[v])
if(w is marked "new")
add(v,w) to T;
Search(w);
}
时间复杂度为O(max(n,e))
广度优先搜索
当到达某一顶点v时,一次考察与v相邻的全部顶点,并访问其中没有访问过的顶点。
算法如下:
BFSTraverse(G)
{
T = Φ ;
count = 1;
for(all v in V )
mark v "new";
while(there exists a vertex v in V marked "new")
BSearch(v);
}
void BSearch(v)
{
MakeNull(Q); // 空队列
bfn[v] = count;
count ++;
mark v "old";
EnQueue(v,Q);
while(!Empty(Q)) {
v = Front(Q);
DeQueue(Q);
for(each w in L[v]) {
if(w is marked "new") {
bfn[w] = count;
count ++ ;
mark w "old";
EnQueue(w,Q);
Insert((v,w),T);
}
}
}
}
无向图深度优先生成森林和广度优先生成森林
在深度(广度)优先搜索过程中,按搜索的顺序对图中的顶点进行深度(广度)优先编号,将图G=(V,E)中的E分成树边和非树边两类。这样,由树边和树边所连顶点所组成的子图S=(V,T),称其为G的深度(广度)优先生成森林。
深度(广度)优先生成森林中的每棵树,叫做G的一棵深度(广度)优先生成树;它对应G的一个连通子图,称为G的一个连通分量。因此,如果一个无向图是连通的,那么只会得到一棵深度(广度)优先生成树。
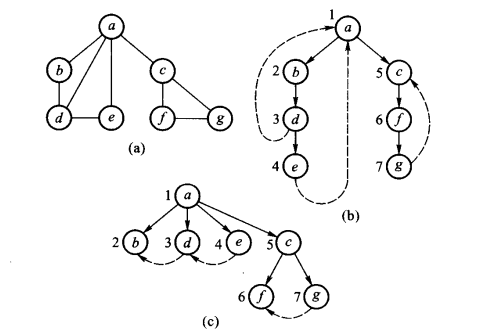
- 深度优先生成森林
分成树边和回退边。设v是当前访问过的顶点,若下一个搜索到的顶点w为new,则(v,w)为树边,若w为old且w是v的父亲,则此时(v,w)已经在T中,已经为树边了;若w是old,且dfn[v] - dnf[w] > 1,即w不是v的父亲,则(v,w)是回退边,用虚线表示。
- 广度优先生成森林
分成树边和横边。树边是编号较小的顶点指向编号较大的顶点,横边是编号较大的顶点指向编号较小的顶点,横边有虚线表示。
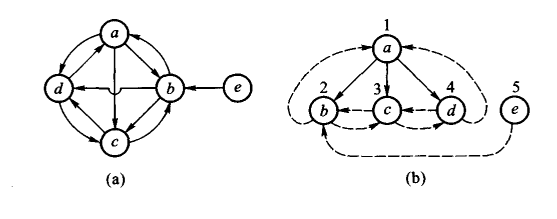
有向图深度优先生成森林和广度优先生成森林
- 深度优先搜索
所有边分成树边、向前边、回退边和横边四种。只有树边是用实线表示,它们的区别如下:
- 树边:搜索过程中, 边(v,w),dfn[v] < dfn[w],且v为old,w为new
- 向前边:和树边一样,只是v为old,w也为old
- 回退边:dfn[v] > dfn[w],且v沿着树边向上能找到w
- 横边:找不到w
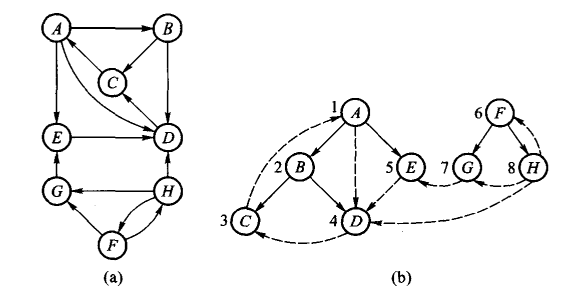
- 广度优先搜索
分成树边、回退边和横边三类。与深度的区别是,横边可能从广度优先编号小的顶点指向编号大的顶点。