1. 拓扑排序
不存在有向环路的有向图称为无环路有向图。无环有向图可用于表示偏序集。设R是有穷集合X上的偏序关系,对X的每个v,用一个以v为标号的顶点表示,由此构成顶点集V。对R中任意一个序对(a,b),a不等于b,由对应的两个顶点建立一条边(a,b),由此构成边集E,则G=(V,E)是无环路有向图。
下面介绍由广度优先搜索算法演变而得到的拓扑排序算法。
给定一个无环路有向图G=(V,E),各顶点的编号为V={1,2,...,n}。要求用label[i]对每个顶点i重新进行编号,使得若i是j的前导顶点(广度优先搜索),则label[i] < label[j]。即拓扑排序是将无环路有向图的每个顶点排成一个线性序列,使得当从顶点i到顶点j存在一条边时,则在线性序列中,将i排在j的前面。
代码如下:
//输入为邻接表
void TopoOrder(GRAPH L)
{
QUEUE Q;
vertex v,w;
int nodecount;
MakeNull(Q);
//入度为0的顶点进队
for(v=1;v<=n;v++)
if(indegree[v]=0)
EnQueue(v,Q);
nodecount = 0;
while(!Empty(Q)) {
v = Front(Q);
DeQueue(Q);
count << v;
nodecount ++;
for(邻接于v的每个顶点w) {
indegree[w] = indegree[w] - 1;//删除由v发出的边
if(indegree[w] == 0)
EnQueue(w,Q);
}
}
if(nodecount < n)
cout << "you huan lu a!";
}
2. 关键路径
2.1 概念
在引进“关键路径”这个词之前,先介绍一下与它密不可分的几个概念。如果在带权的有向图中,用顶点表示事件,边表示活动,权表示活动持续的时间。把这样的有向图称为关于边的活动网。与之相对应,若用顶点表示活动,用边表示活动的先后顺序关系,这样的有向图称为关于顶点的活动网,例如拓扑图。将这些活动网统称为AOE网。
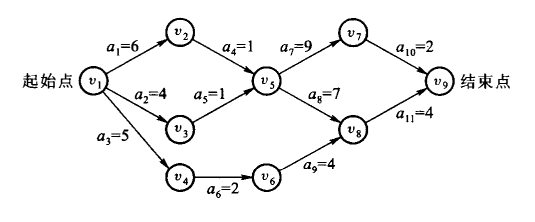
事件v5表示活动a4和a5已结结束,a7和a8可以开始。边上的数字为持续的时间。
显然,在AOE网中,由于有些活动可以同时进行,所以完成工程最小时间是从起始点到结束点最长路径的长度,把从起始点到结束点具有最大长度的路径称为关键路径。图中的a1-a4-a7-a10(长为18)就是其中一条关键路径。关键路径的长度代表完成这个工程最少需要的时间。这里需要注意,活动的时间只是指完成该活动的最少时间,实际上可能会拖延什么的。
从AOE网的起始点v1到其中某一顶点vi的最长路径的长度,称为事件vi的最早发生时间,记为VE[i]。如事件v5的最早发生时间为7。
用E(i)表示活动ai的最早开始时间。事件vi的最早发生时间决定了以vi为起点的所有边上的活动的最早开始时间。如E(7)=E(8)=事件v5的最早发生时间=7。
对于活动ai,还定义一个最迟开始时间,它是不使整个工程的完成时间拖延的最晚开始时间。用L(i)表示。如,L(6)=18-a11-a9-a6=8。
对于事件vi,也有一个最迟发生时间VL[i]。
关键路径上,所有活动都满足E(i) = L(i),把满足这一等式的所有活动称为
关键活动。
活动ai的最迟开始时间和最早开始时间之差表示ai的完成时间余量,即允许ai延缓的时间。
2.2 寻找关键活动
求解关键活动在于求解E(i)和L(i)。
设活动ai所对应的边为(k,m),并且用ACT[k][m]来表示一个活动的持续时间,很明显:
E(i) = VE[k] 或者用E(k,m)
L(i) = VL[m] - ACT[k][m] 或者用L(k,m)
现在就转化为求解VE[i]和VL[i],分成两步:
- 前进阶段:从VE1=0开始,沿着路径上每条边的方向,应用如下公式求出每个事件的最早发生时间:
VE[m] = max{VE[k]+ACT[k][m]},k是m的直接前导顶点 - 回退阶段:从已求出的VL[n]=VE[n]开始,沿着路径上每条边的相反方向,应用如下公式:
VL[k] = min{VL[m]-ACT[k][m]},m为k的直接后续顶点
可以用类似拓扑排序的算法求出L[i]和E[i],对于这两者都相等的活动则是关键活动,将所有非关键活动删除后得到的图,任意一条路径都是关键路径。