C. Celex Update
题意
有一个无限大的表格,按照某个方式填上数字。给出T个询问,每个询问
给出两个坐标((x1,y1),(x2,y2)),只能向下或者向右移动,问从第一个点移动
到第二个点,有多少种不同的路径和。
题解
直接猜的是,所有路径和都不相同。
写组合公式的时候,突然想到这个答案 有点大啊,题目也没有说取模。
脑子瓦特了,竟然写了交了,GG。
肯定会有重复的。
比如((1,1)->(3,3))
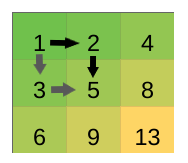
1 2 5 9 13
1 3 5 8 13
这两条路径就是一样的,因为向下走比向右走会多1。
这样就可以抵消影响,使得和一样。
这时就大胆的猜,路径和最小值和路径和最大值之间是不是都可以取到。
在之前某一路径某个向右走的地方选择向下走,就可以使得路径和增加1。
都可以取到,答案就是最大值和最小值的差+1。
让(disx=x2-x1),(disy=y2-y1),(maxn=min(disx,disy))
此时最大路径和最小路径 每个值的差值依次是(1,2,3,...,maxn-1,maxn,...,maxn,maxn-1,..,4,3,2,1)
数字总个数是(x2-x1+y2-y1-1),即一条路径长度-2
求和之后+1就是((x2-x1)*(y2-y1)+1)
代码
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10;
typedef long long ll;
typedef unsigned long long ull;
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
int x1,y1,x2,y2;
scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
int x=x2-x1,y=y2-y1;
printf("%lld
",1LL*x*y+1);
}
return 0;
}