LCG算法
djb2与LCG很类似,故先介绍 LCG。
LCG(linear congruential generator)算法是一个古老的产生随机数的算法。由以下参数产生
| 参数 | m | a | c | X |
|---|---|---|---|---|
| 性质 | 模数 | 乘数 | 加数 | 随机数 |
| 作用 | 取模 | 移位 | 偏移 | 作为结果 |
LCG算法是如下的一个递推公式,每下一个随机数是当前随机数向左移动 log2 a 位,加上一个 c,最后对 m 取余,使随机数限制在 0 ~ m-1 内
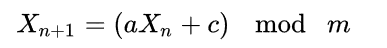
从该式可以看出,该算法由于构成简单,具有以下优点:
- 计算速度快
- 易于实现
- 易于写入硬件
以下是针对不同参数 lcg 产生随机数的效果图
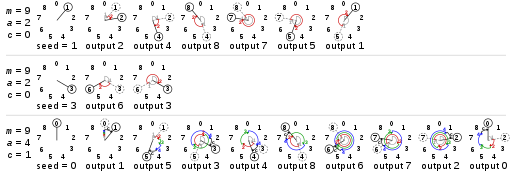
可以看出,针对不同的参数,lcg产生的效果差别很大
以下是针对不同环境下的参数选择
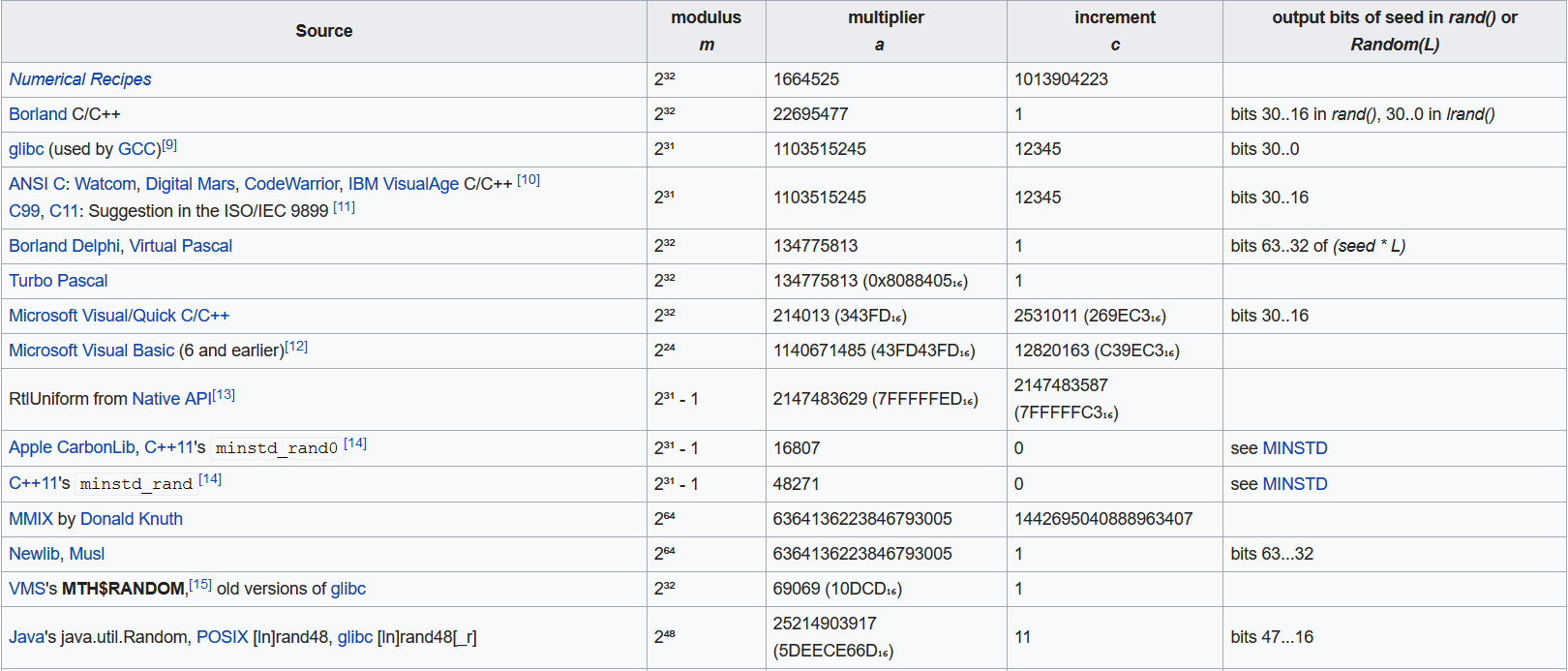
示例代码
def lcg(modulus, a, c, seed):
while True:
seed = (a * seed + c) % modulus
yield seed
djb2
djb2是一个产生随机分布的的哈希函数,与LCG的算法相似。
以下是 djb2 的哈希函数:
X = (a * X) + c; // "mod M", M = 2^32 或 2^64
示例代码
// generates a hash value for a sting
// same as djb2 hash function
//构造哈希函数 f(hash)= hash * 33 + c
unsigned int CountMinSketch::hashstr(const char *str) {
unsigned long hash = 5381;
int c;
while (c = *str++) {
hash = ((hash << 5) + hash) + c; /* hash * 33 + c */
}
return hash;
}
本部分利用djb2处理字符串。
其中参数常有以下取值:
M=2^32
M常取一个较大的质数,以减少冲突。
由于哈希函数构造简单,使用移位和相加的操作,所以计算速度快。
要注意hash值的计算,在不同机器上,可能会造成溢出的问题,可以及时对hash值取余。但是会增加计算开销,造成hash范围减小的问题。
为什么选择参数33和
33 was chosen because:
-
乘法易于移位或相加
-
从移位和加法实现中可以看到,使用33可以复制散列累加器中的大多数输入位,然后将这些位相对地分散开来。这有助于形成好的雪崩现象。使用较大的移位将复制更少的位,使用较小的移位将使位交互更局部,并使交互扩展所需的时间更长。
-
32 = 2^5,32 与移 5 位相关,有助于将每一个字符串的每一位比特都作用到最终的哈希值当中
-
在考虑ASCII字符数据时,5的移位是一个很好的移位量。ASCII字符可以看作是4位字符类型选择器和4位字符类型选择器。前4位的数字都是0x3。因此,8位移位将导致具有特定含义的位与具有相同含义的其他位相互作用。4位或2位的移位同样会在相似的位之间产生强烈的交互作用。5位的移位使得一个字符的4个低阶位中的许多位与同一字符的4个上位中的许多强相互作用。
5381 was chosen because
- 选择5381并不太重要,很多其他的大的质数数也可以运行地很好。
哈希选择参考
源自 https://stackoverflow.com/questions/1579721/why-are-5381-and-33-so-important-in-the-djb2-algorithm
djb2不是一个快速哈希函数,因为它每次处理输入一个字符,并且不尝试使用指令级并行。
在现代处理器,乘法时该算法要快得多了乘法和其他因素(如2 ^ 13 + 2 ^ 5 + 1)可能也有类似的表现,有更好的输出,更容易写。
一个好的非加密哈希函数不希望产生随机输出。相反,给定两个几乎完全相同的输入,它希望产生完全不同的输出。
如果你的输入值是随机分布的,你不需要一个好的哈希函数,你可以使用你输入的任意一组比特。一些现代哈希函数(Jenkins 3, Murmur, probably CityHash)产生的输出分布比高度相似的随机输入更好。
选择哈希函数的详细博客 https://blog.csdn.net/xu20082100226/article/details/52651212