栅栏加密 国内国外不一样？

这是一道CTF题引发的思考

很多国内的博客包括百度百科说的栅栏加密是这样的

 1 2 3 4 5 6 # key=3 进行栅栏加密

 1 2 3 
 4 5 6

结果为 1 4 2 5 3 6

但是在查国外的栅栏加密（Rail-fence Cipher）

1 2 3 4 5 6 # key=3 Rail-fence Cipher

1 . . . 5 .     ↘　　　　 　↗ ↘
. 2 . 4 . 6　　　　↘　　  ↗
. . 3 . . .　　　　  ↘ ↗

结果为 1 5 2 4 6 3

http://www.practicalcryptography.com/ciphers/classical-era/rail-fence/

为什么会想到查这个？

按照第一种加密方式，也就是国内普遍定义的（当然有些博客除外）

　　假设：

　　　　有字符串C，len(C) = n， n = p * q

　　则有：

　　　　C 栅栏加密（key=p） == C栅栏解密（key=q）

　　具体例子：

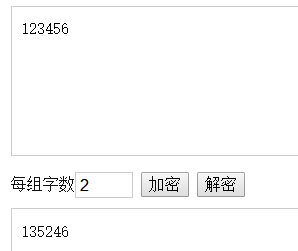
 即 123456栅栏加密（key=2） => 135246

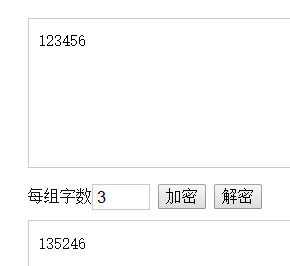
 123456 栅栏解密（key=3） =>135246

  两个结果相同

  也就是说，按照这种定义，是存在另一个key值，使得加密解密效果相同，可以称其为“补key”，（好吧我瞎起的名，理解就好）

  如果某字符串C，是使用这种定义方式，不管是用key加密或者解密，我都可以一直使用栅栏解密，遍历key范围[2，len(C)-1]，暴力求解。

  有的工具是分解len(c)的因子，把除1以外的因子，当做key，进行暴力求解。

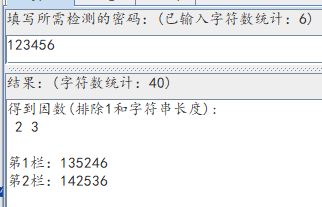
 我说的是比较广义的，即对len(C)的因子不包括key的情况，涉及到对C的padding

1234567    key=4 加密

padding:1234567x （4|8  key|len(c)
拆分：(1,2,3,4)(5,6,7,x)
1 2 3 4
5 6 7 x

结果为1526374（padding的x跳过）

------------------------------------

1526374    key=4 解密

padding:1526374x （4|8  key|len(c)）
拆分：(1,5)(2,6)(3,7)(4,x)
1 2 3 4
5 6 7 x

结果为1234567（padding的x跳过）

-----------------------------------

 为什么扯这些，是因为有一道题，经过这种遍历key的办法无法还原

例如：

fiasl_miasp_galn{_e_te}xh

 长度为25

根据因子是不行的，只能爆破key

你会发现，1试到24都不能拿到正确的flag

failans{l__em_itaes}px_hg
fs_ipea__sgtlae_l}mnxi{ha
fia_ialtasnesp{}l__x_gehm
f_pntim_{eaig_}saaexlsl_h
f_sa_eimple}ai_n_xsag{thl
flag{_}i_sa_txampleehsi_n
flipa{_}i_a_l_txamsgneehs
fsmsgneexilipa{_}ha_a_l_t
fsmsgn__exilipa{et}ha_a_l
fsms_an__exilipgl{et}ha_a
fs_is_an__exilmapgl{et}ha
falmapgl{et}his_is_an__ex
falmapgl{et}xhis_is_an__e
falmapgl{ete}xhis_is_an__
falmapgl{e_te}xhis_is_an_
falmapgl{_e_te}xhis_is_an
falmapgln{_e_te}xhis_is_a
falmapgaln{_e_te}xhis_is_
falmap_galn{_e_te}xhis_is
falmasp_galn{_e_te}xhis_i
falmiasp_galn{_e_te}xhis_
fal_miasp_galn{_e_te}xhis
fasl_miasp_galn{_e_te}xhi

　　

 因为这个串采用的是第二种方式，

 并且这种方式是不存在 '补key'的

 只能用第二种方式key=3进行加密才能还原，对是加密！

 fiasl_miasp_galn{_e_te}xh （Rail-fence Cipher 加密 key= 3）

=>

flag{this_is_an__example}

方式二的 在线工具

http://ctf.ssleye.com/railfence.html