第1章 数据结构绪论
第2章 算法
第3章 线性表
第4章 栈与队列
第5章 串
第6章 树
第7章 图
第8章 查找
第9章 排序
第1章 数据结构绪论
数据结构:是相互之间存在一种或多种特定关系的数据元素的集合。
1.1基本概念术语
1.1.1 数据
数据:是描述客观事物的符号,是计算机中可以操作的对象,是能被计算机识别,并输入给计算机处理的符号集合。
数据不仅仅包括整型、实型等数值类型,还包括字符及声音、图像、视频等非数值类型。这里所说的数据就是符号,这些符号具备两个前提:
*可以输入到计算机中
*能被计算机程序处理
对于整型、实型等数值类型,可以进行数值计算。
对于字符数据类型,就需要进行非数值的处理。声音、图像、视频等可以通过编码的手段变成字符数据来处理。
1.1.2 数据元素
数据元素:是组成数据的、有一定意义的基本单位,在计算机中通常作为整体处理。也被称为记录。
如:人类中,什么是数据元素?当然是人
1.1.3 数据项
数据项:一个数据元素可以由若干个数据项组成。
如 人这样的数据元素,可以有眼、耳、鼻、嘴、手、脚这些数据项,也可以有姓名、年龄、性别、出生地址、联系电话等数据项。
数据项是数据不可分割的最小单位。
1.1.4 数据对象
数据对象:是性质相同的数据元素的集合,是数据的子集。
1.1.5 数据结构
数据结构:是相互之间存在一种或多种特定关系的数据元素的集合。
在计算机中,数据元素并不是孤立、杂乱无序的,而是具有内在联系的数据集合。数据元素之间存在的一种或多种特定关系,也就是数据的组织形式。
1.2 逻辑结构与物理结构
1.2.1 逻辑结构
逻辑结构:是指数据对象中数据元素之间的相互关系。逻辑结构氛围以下四种:
1.集合结构
集合结构中的数据元素除了同属一个集合外,它们之间没有其他关系。各个数据元素是“平等”的,它们的共同属性是“同属于一个集合”。数据结构中的集合关系就类似于数学中的集合
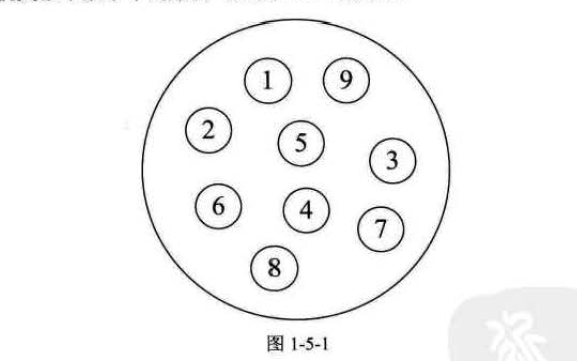
2.线性结构
线性结构:线性结构中的数据元素之间是一对一的关系

3.树形结构
树形结构中的数据元素之间存在一种一对多的层次关系
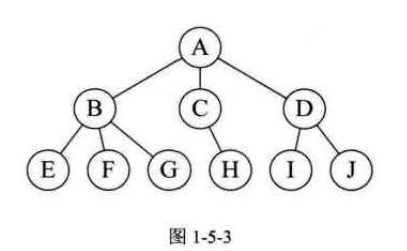
4.图形结构
图形结构的数据元素是多对多的关系

1.2.2 物理结构
物理结构:是指数据的逻辑结构在计算机中的存储形式。
数据是数据元素的集合,那么根据物理结构的定义,实际上就是如何把数据元素存储到计算机的存储器中。存储器主要是针对内存而言的,像硬盘、软盘、光盘等外部存储器的数据组织通常用文件结构来描述。
数据的存储结构应正确反映数据元素之间的逻辑关系,这才是最为关键的,如何存储数据元素之间的逻辑关系,是实现物理结构的重点和难点。
数据元素的存储结构形式有两种:顺序存储 和 链式存储。
1. 顺序存储结构
顺序存储结构:是把数据元素存放在地址连续的存储单元里,其数据间的逻辑关系和物理关系是一致的

这种存储结构就是排队占位。数组就是这样的顺序存储结构。当告诉计算机要建立一个有 9 个整型数据的数组时,计算机就在内存中找了片空地,按照一个整型所占位置的大小乘以9,开辟一段连续的空间,于是第一个数组数据就放在第一个位置,第二个数据放在第二个,这样依次摆放。
2. 链式存储结构
链式存储结构:是把数据元素存放在任意的存储单元里,这组存储单元可以是连续的,也可以是不连续的。
数据元素的存储关系并不能反映其逻辑关系,因此需要用一个指针存放数据元素的地址,这样用过地址就可以找到相关联数据元素的位置。
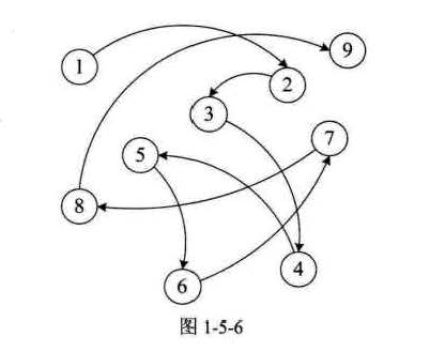
链式存储比较灵活,数据存在哪里不重要,只要有一个指针存放了相应的地址就能找到。
逻辑结构是面向问题的,而物理结构就是面向计算机的,其基本的目标就是将数据及其逻辑关系存储到计算机的内存中。
1.3 抽象数据类型
1.3.1 数据类型
数据类型:是指一组性质相同的值的集合及定义在此集合上的一些操作的总称。
数据类型是按照值的不同进行划分的。在高级语言中,每个变量、常量和表达式都有各自的取值范围。类型就用来说明变量或表达式的取值范围和所能进行的操作。
C语言中,按照取值不同,数据类型可以分为两类:
原子类型:是不可以再分解的基本类型,包括整型、实型、字符型等。
结构类型:由若干个类型组合而成,是可以再分解的。例如,整型数组是由若干整型数据组成的。
1.3.2 抽象数据类型
对已有的数据类型进行抽象,就有了抽象数据类型。
抽象数据类型:是指一个数学模型及定义在该模型上的一组操作。抽象数据类型的定义仅取决于它的一组逻辑特性,而与其在计算机内部如何表示和实现无关。
一个抽象数据类型定义了:一个数据对象、数据对象中各数据元素之间的关系及对数据元素的操作。
总结:
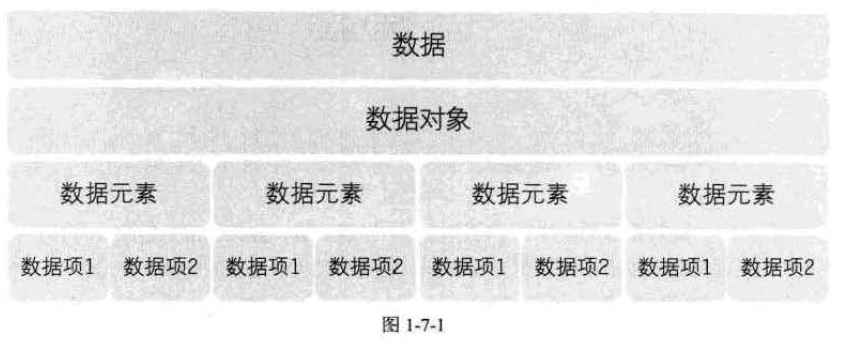
由上述概念给出数据结构的定义:数据结构是相互之间存在一种或多种特定关系的数据元素的集合。
