个人项目作业
| Q | A |
|---|---|
| 这个作业属于哪个课程 | 2020春季计算机学院软件工程(罗杰 任健) |
| 这个作业的要求在哪里 | 个人项目作业 |
| 我在这个课程的目标是 | 系统地学习软件工程开发知识,掌握相关流程和技术,提升工程化开发的能力 |
| 这个作业在哪个具体方面帮助我实现目标 | 了解熟悉个人软件开发流程(PSP) |
| 教学班级 | 005 |
| 项目地址 | https://github.com/NNNNNF/intersect.git |
PSP表格:
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | ||
| · Estimate | · 估计这个任务需要多少时间 | 10 | 10 |
| Development | 开发 | ||
| · Analysis | · 需求分析 (包括学习新技术) | 60 | 120 |
| · Design Spec | · 生成设计文档 | 20 | 30 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 0 | |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 20 | 20 |
| · Design | · 具体设计 | 20 | 30 |
| · Coding | · 具体编码 | 60 | 80 |
| · Code Review | · 代码复审 | 20 | 30 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 100 | 120 |
| Reporting | 报告 | ||
| · Test Report | · 测试报告 | 60 | 60 |
| · Size Measurement | · 计算工作量 | 30 | 30 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 30 | 50 |
| 合计 | 430 | 580 |
解题思路
-
对题目中的给出的条件((x_1,y_1))和((x_2,y_2)),首先想到的是求取直线表达式,我采取的表达方式是:
(l:ax+by+c=0),利用已知两个点的坐标可以比较容易的求出(a,b,c)的值:
(a=y_1-y_2),(b=x_2-x_1),(c=x_1y_2-x_2y_1),由于直线组中的每两条直线都需要求交点,所以选择记录(a,b,c)的值来存储直线。
-
然后是求交点。根据两条直线方程(l_1:a_1x+b_1y+c_1=0)和(l_2:a_2x+b_2y+c_2=0)可求得交点坐标为:
(x=frac{c_2b_1-c_1b_2}{a_1b_2-a_2b_1},y=frac{c_1a_2-c_2a_1}{a_1b_2-a_2b_1}),此时涉及到分母为0的情况,即两直线平行,交点个数为0;故在对任意两直线求交点前,先判断其是否平行,若不平行才进行求交点计算。
-
最后是关于直线和点选择什么样的容器存储的问题,考虑到点集会有重复,所以在vetor和set之间,选择了可以确保容器内有不重复元素的set(参考资料),此时也涉及到了运算符重载的问题,以确保set容器中不存在重复点。
-
对于附加题添加圆的问题中,在原来的基础上增加了圆和圆之间的交点,圆和直线的交点。若圆和圆之间有交点,那么两个圆的方程可确定一条过交点的直线,经过转化仅需添加圆和直线交点的相关函数。对于圆方程({(x-ca)^2}+{(y-cb)^2}=cr^2),其中圆心为((ca,cb)),半径为(cr),联立直线方程(ax+by+c=0)可得方程组,方程是否有解即对应了圆和直线是否存在交点,可通过判断delta得到;求解方程组即可算出交点坐标。
设计实现
- 在实现过程中设计了三个类,一个是Point,一个是Line,还有一个是Circle,因为Line的3个参数(a,b,c)是由两个点的坐标计算而来,故Line继承自Point。由于三个类涉及到的参数和计算都不算复杂,所以关于Point和Line,Circle的函数都放置在assis.h中。
- 需要实现的重要函数有以下:1.求直线参数;2.判断直线是否相交;3.求直线交点;4.set用于去重的运算符重载函数;5.判断圆是否有交点;6.求解圆和直线相交的交点。所有的函数由main函数调用。
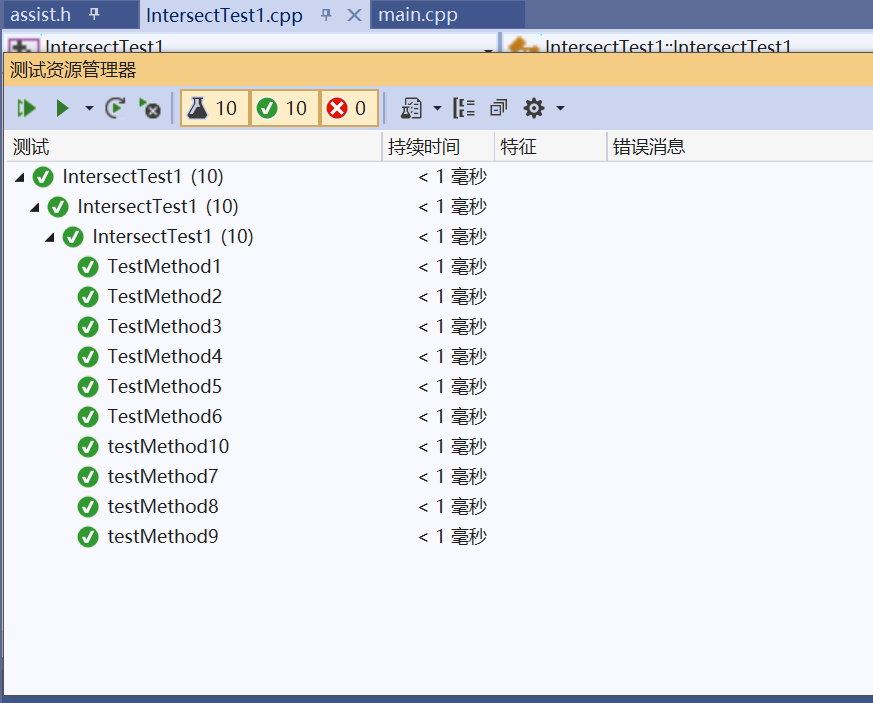
- 关于单元测试,我主要设计了对点和直线的构造函数、求直线表达式函数、判断直线是否相交函数的测试数据,对无重复交点的直线集合、有重复交点的直线集合,无交点直线集合,临界数据几种情况进行测试。
- 附加题中增加了对圆的相交、相切、相离几种情况以及直线和圆相交、相切、相离的判断。
程序性能
总共花费时间:60分钟
一开始想的是等所有直线输入完成再开始计算交点,其实可以一边输入一边对直线交点进行处理。即一开始直线容器(lines)为空,对输入的直线(l)或圆(c),先与(lines)中所有直线求交点,所有圆求交点,若存在则insert到点集容器(points)中,然后将直线(l)存储到(lines)中,圆(c)存储到(circles)中,再接着输入,这样可以减小循环开销。
性能分析:
在数据量为1000时的性能分析:
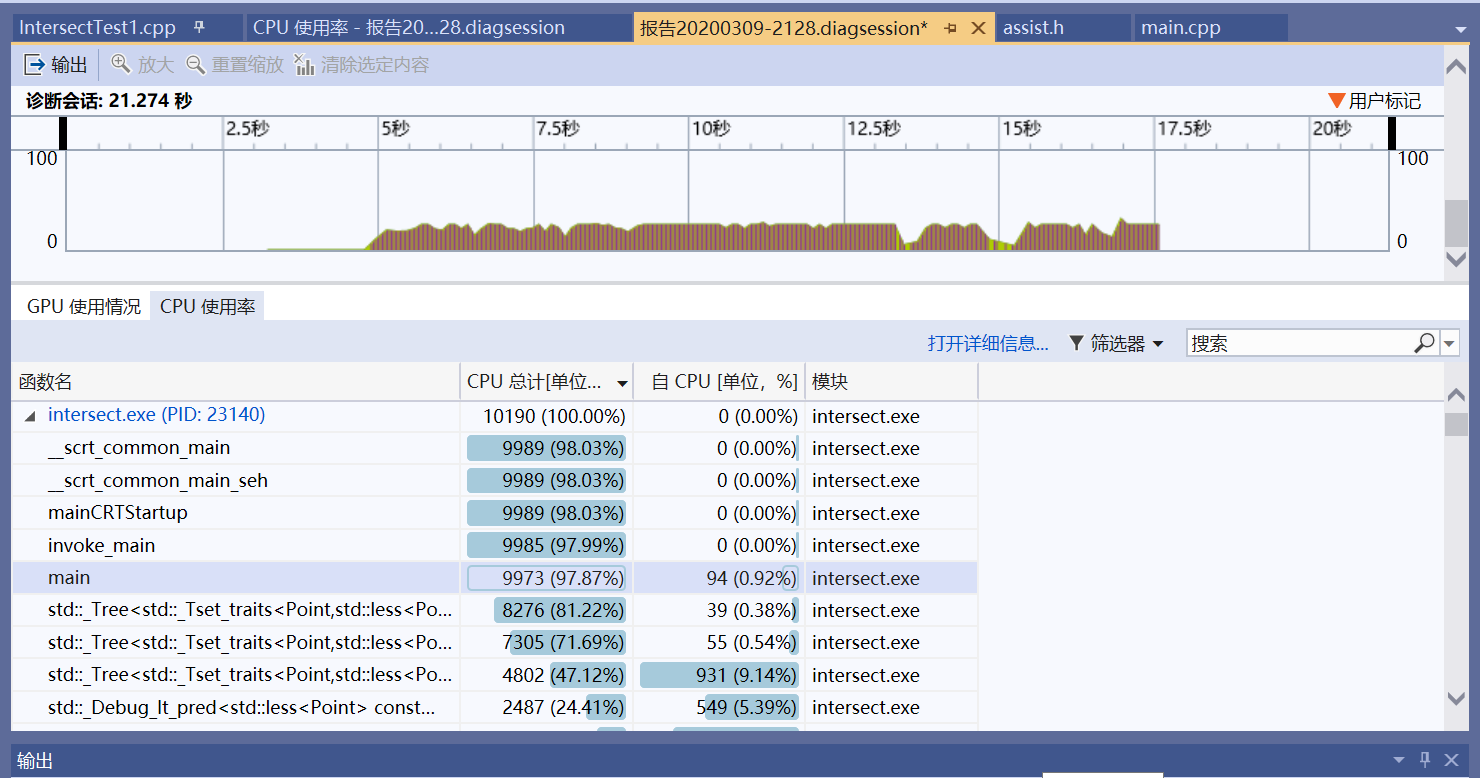
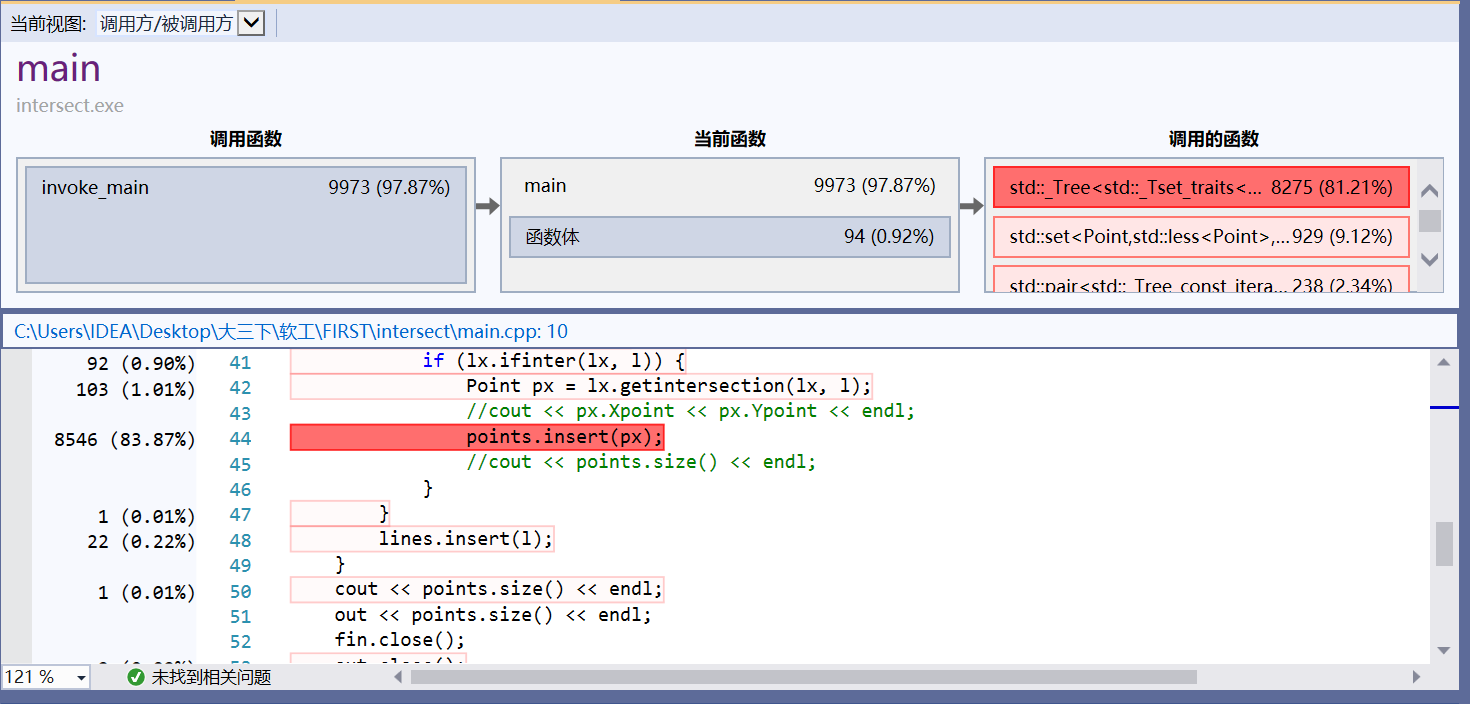
由下图可以看出程序中消耗最大的操作是set容器的insert操作:
代码说明
- Line类
class Line :public Point {
public:
double a = 0;
double b = 0;
double c = 0;
public:
//计算a,b,c
Line getLine(Point pt1, Point pt2);
//获得交点
Point getintersection(Line l1, Line l2);
//是否相交
bool ifinter(Line l1, Line l2);
//单元测试
string showLine();
//重载操作符
bool operator < (const Line& lx) const
{
if (a != lx.a) {
return a < lx.a;
}
else if (b != lx.b) {
return b < lx.b;
}
else {
return c < lx.c;
}
}
};
- 求交点
inline Point Line::getintersection(Line l1, Line l2) {
Point result;
double mid = l1.a * l2.b - l2.a * l1.b;
result.Xpoint = (l2.c * l1.b - l1.c * l2.b) / mid;
result.Ypoint = (l1.c * l2.a - l2.c * l1.a) / mid;
return result;
}
- Circle类
class Circle {
public:
double Xpoint = 0;
double Ypoint = 0;
double r = 0;
public:
Circle() {}
Circle(double x, double y,double r) {
Xpoint = x;
Ypoint = y;
r = r;
}
bool operator<(const Circle& a)const
{
if (Xpoint != a.Xpoint) {
return Xpoint < a.Xpoint;
}
else if (Ypoint != a.Ypoint) {
return Ypoint < a.Ypoint;
}
else {
return r<a.r;
}
}
bool operator == (const Circle& p) const
{
if (Xpoint != p.Xpoint) {
return false;
}
else if (Ypoint != p.Ypoint) {
return false;
}
else {
return r == p.r;
}
}
//圆和圆是否相交
bool ccifinter(Circle c1, Circle c2);
//圆和直线交点
bool clifinter(Circle c, Line l);
//计算圆与1圆交点确定的直线
Line getCCline(Circle c1, Circle c2);
};
- 计算圆和直线交点
bool Circle::clifinter(Circle c, Line l) {
double cx = c.Xpoint;
double cy = c.Ypoint;
double cr = c.r;
double la = l.a;
double lb = l.b;
double lc = l.c;
double d = fabs(la * cx + lb * cy + lc) / sqrt(la * la + lb * lb);
if (d > c.r) {
return false;
}
else if(lb==0){
double parax = -1.0 * lc / la;
double paray = cr * cr - cx * cx - (lc * lc + 2 * lc * la * cx) / (la * la);
Point pt1;
Point pt2;
pt1.Xpoint = parax;
pt1.Ypoint = cy + sqrt(paray);
pt2.Xpoint = parax;
pt2.Ypoint = cy - sqrt(paray);
points.insert(pt1);
points.insert(pt2);
//cout << pt1.Xpoint << " " << pt1.Ypoint << endl;
//cout << pt2.Xpoint << " " << pt2.Ypoint << endl;
}
else {
double paraa = la * la + lb * lb;
double parab = -2.0 * lb * lb * cx + 2 * la * lc + 2 * la * lb * cy;
double parac = lb * lb * cx * cx + (lc + cy * lb) * (lc + cy * lb) - cr * cr * lb * lb;
double deta = sqrt(parab * parab - 4 * paraa * parac);//(b^2-4ac)^1/2
Point pt1;
Point pt2;
pt1.Xpoint = (-1.0 * parab + deta) /( 2 * paraa);
pt1.Ypoint = (-1.0 * la * pt1.Xpoint - lc) / lb;
pt2.Xpoint = (-1.0 * parab - deta) /( 2 * paraa);
pt1.Ypoint = (-1.0 * la * pt2.Xpoint - lc) / lb;
points.insert(pt1);
points.insert(pt2);
//cout << pt1.Xpoint << " " << pt1.Ypoint << endl;
//cout << pt2.Xpoint << " " << pt2.Ypoint << endl;
}
return true;
}
- main函数
if (L == 'L') {
fin >> x1 >> y1 >> x2 >> y2;
Point pt1, pt2;
pt1.Xpoint = x1;
pt1.Ypoint = y1;
pt2.Xpoint = x2;
pt2.Ypoint = y2;
Line l = l.getLine(pt1, pt2);
for (Line lx : lines) {
if (lx.ifinter(lx, l)) {//判断是否平行
Point px = lx.getintersection(lx, l);//求交点
points.insert(px);//插入点集合
}
}
for (Circle c : circles) {
c.clifinter(c, l);
}
lines.insert(l);
}
if (L == 'C') {
int cx, cy,cr;
fin >> cx >> cy >> cr;
Circle c;
c.Xpoint = cx;
c.Ypoint = cy;
c.r = cr;
for (Line lx : lines) {
c.clifinter(c, lx);//求直线和圆交点
}
for (Circle cc : circles) {
if (c.ccifinter(c, cc)) {//判断是否相交
Line l = c.getCCline(c, cc); //获得直线
c.clifinter(c, l);//求解交点
}
}
circles.insert(c);
}
}
单元测试和Code Quality Analysis