机器学习笔记（二）线性回归模型实现

一、向量化

对于大量的求和运算，向量化思想往往能提高计算效率（利用线性代数运算库），无论我们在使用MATLAB、Java等任何高级语言来编写代码。

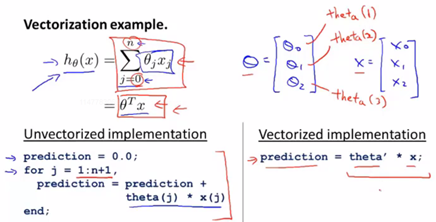
运算思想及代码对比

 

的同步更新过程向量化

 

向量化后的式子表示成为：

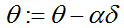
其中是一个向量，是一个实数，是一个向量，所以在这里是做一个向量的减法。在将计算向量化的同时，这种运算方式使我们很好地实现了的同步更新，我自行推导了一下，体会运算过程中的同步更新是如何实现。

 

 

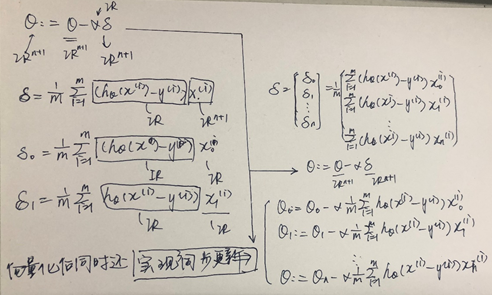
二、 简单一元线性回归实现

数据：是房子的大小（平方英尺）和房价（美元）之间的对应关系。

练习：Matlab实现

%简单一元线性回归练习
theta_0 = 0;
theta_1 = 0;
alpha = 0.000001;
x = [150; 200; 250; 300; 350; 400; 600];
y = [6450; 7450; 8450; 9450; 11450; 15450; 18450];
%画出点
plot(x, y, 'r*', 'MarkerSize', 8); % 5控制*的大小
hold on;

counter = 50;
[theta_0, theta_1] = gradientDescent_LOW(x, y, theta_0, theta_1, alpha, counter);
b = theta_0 + theta_1 * x;
%画出拟合直线
plot(x, b, 'b-', 'Linewidth',2); % 5控制*的大小
hold on;
xlabel('面积/平方英尺');
ylabel('房价/美元');
title('一元线性回归');

function [theta_0, theta_1] = gradientDescent_LOW(x, y, theta_0, theta_1, alpha, counter)
%此处x为向量
m = length(y); %样本数量

for iter = 1:counter
    H = theta_0 + theta_1 * x; %线性假设函数
    
    %计算代价函数输出
    res = 0;
    for i = 1:m
        res = res + (H(i)-y(i))^2;
    end
    Jtheta = res/(2*m)
    
    %更新theta_0
    sum = [0;0]; %记录两个偏导部分（求和过程）
    for i = 1:m
        sum(1,1) = sum(1,1) + (H(i)-y(i));
    end
    theta_0 = theta_0 - alpha * sum(1,1)/m;
    %更新theta_1
    for i = 1:m
        sum(2,1) = sum(2,1) + (H(i)-y(i)) * x(i);
    end
    theta_1 = theta_1 - alpha* sum(2,1)/ m ;
    
 end

得到拟合图像：

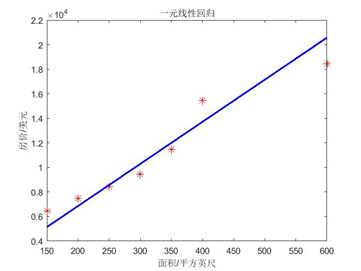
提出问题：

1. 使alpha、counter取值规范

加入特征缩放后，alpha取0.03，counter = 1500。能够达到较好的拟合效果。

%特征缩放
for i = 1:length(y)
    x(i) = (x(i)-min(x))/(max(x)-min(x))
    y(i) = (y(i)-min(y))/(max(y)-min(y))
end

 

拟合图像

2.  梯度下降迭代结束标志

    a)  定义一个合理的阈值，当两次迭代之间的差值小于该阈值时，迭代结束。

    b) 设置一个大概的迭代步数，比如1000或500。

 三、多元线性回归实现

1. 梯度下降法

数据：波士顿房价数据集（经个别剔除）共419条数据

（理论推导见上一篇笔记，直接上代码）

%test2.m
[Data] = xlsread('Boston house prise.xlsx',1,'A1:M419');
[y] = xlsread('Boston house prise.xlsx',1,'N1:N419');
[m,n] = size(Data); % m样本数量 n特征数
Data = featureScaling(Data);
y = featureScaling(y);
x0 = ones(m,1);

X = ([x0,Data])';

Theta = zeros(n+1,1);
alpha = 0.009;
counter = 1500;
Theta = gradientDescent(X, y, Theta, alpha, counter);
plot(1:m, y, 'r-', 'Linewidth',1); % 5控制*的大小
hold on;
plot(1:m, Theta'*X, 'b-', 'Linewidth',1); % 5控制*的大小
hold on;
xlabel('样例序号');
ylabel('房价');
title('梯度下降-波士顿房价预测');
legend('真实值','预测值');

%梯度下降（矢量化）
function [Theta] = gradientDescent(X, y, Theta, alpha, counter)
% X Theta 均为矩阵
[m,n] = size(X); % m样本数量 n特征数
J_history = zeros(counter, 1);
for iter = 1:counter
    H = Theta' * X; %线性假设函数
    Delta = 1/m * X *(H'-y);
    Theta = Theta - alpha * Delta;
    % 保存下所有J，可以查看收敛情况
    res = 0;
    for i = 1:m
        res = res + (H(i)-y(i))^2;
    end
    J_history(iter) = res/(2*m);
end
J_history
end

%特征放缩
function [X] = featureScaling(X)
%X 为矩阵，每一列为一组特征值
[m,n] = size(X);
for j = 1:n
    for i = 1:m
        X(i,j) = (X(i,j)-min(X(:,j)))*1/(max(X(:,j))-min(X(:,j)));
    end
end

2. 正规方程法

 （理论部分见上一篇笔记）

[X] = xlsread('Boston house prise.xlsx',1,'A1:M419');
[y] = xlsread('Boston house prise.xlsx',1,'N1:N419');
theta = pinv(X'* X)* X'*y
[m,n] = size(X);    % m样本数量 n特征数
plot(1:m, y, 'r-', 'Linewidth',1);   
plot(1:m, theta'*X', 'b-', 'Linewidth',1);  

输出结果：

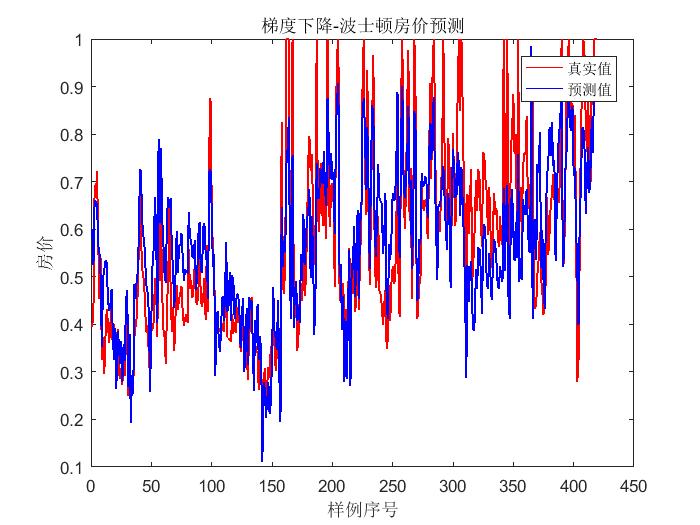
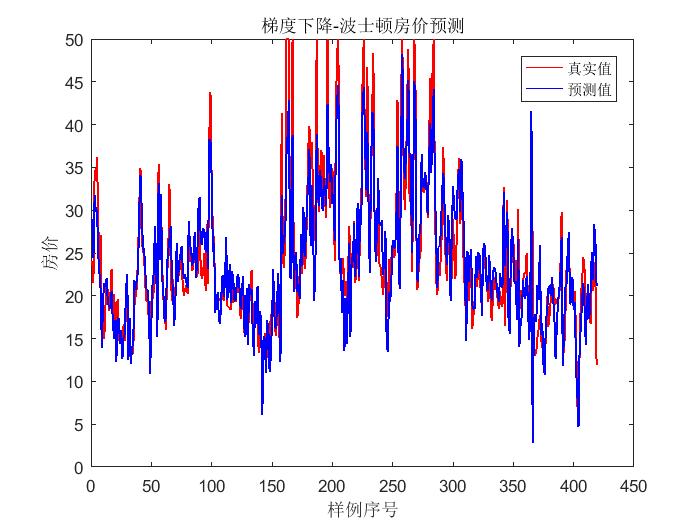
                                梯度下降法                                          正规方程法                                                                            

总结：

1. 在运算中多用矢量化的思想。

2. 在多元线性回归的实现中，随着参数的增多，愈加体现出在梯度下降法当中，参数和初始值选择对结果是有很大影响的。

3. 在本次用波士顿房价数据进行实验的过程中，正规方程法的拟合效果优于梯度下降法。