看到一篇不错的介绍最小二乘法的博客,其中有个idea很不错,在拟合线性函数的时候,求得的函数跟真实函数或者真实数据之间或多或少都会有一个误差。

图中红色直线就是我们求得的线性函数。
为了表示拟合的函数跟真实数据之间的误差,在函数后面添加了个误差项μ

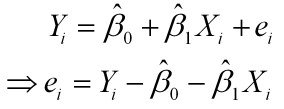
为了使这个总体误差最小,用残差平方和来表示:

则通过Q最小确定这条直线,即确定 ,以
,以 为变量,把它们看作是Q的函数,就变成了一个求极值的问题,可以通过求导数得到。求Q对两个待估参数的偏导数:
为变量,把它们看作是Q的函数,就变成了一个求极值的问题,可以通过求导数得到。求Q对两个待估参数的偏导数:

解得:

最小二乘法vs梯度下降法
1、跟梯度下降法求解回归模型一样,都是以残差平方和最小化作为优化策略。
2、最小二乘法是直接通过矩阵运算(有时候计算很复杂)求解损失函数的极值,而梯度下降法是通过从初始点延梯度方向搜索局部最优值
3、最小二乘法直接使用极值,将极值作为最小值。其假定有二:1,损失函数中极值就是最小值。2,损失函数具有极值。而梯度下降则不同,梯度下降并没有什么假定,是利用函数中某一点的梯度,一步步寻找到损失函数的局部最小值,之后对多个局部最小值进行比较(选定不同的初始值),确定全局最小值。
4、总体来说:最小二乘法计算简单,但梯度下降法更加通用!
参考博客:
http://blog.csdn.net/qll125596718/article/details/8248249
https://www.zhihu.com/question/20822481