poj 2566"Bound Found"(尺取法)

传送门

参考资料：

　　[1]:http://www.voidcn.com/article/p-huucvank-dv.html

题意：

　　题意就是找一个连续的子区间，使它的和的绝对值最接近target。

题解：

　　这题的做法是先预处理出前缀和，然后对前缀和进行排序，再用尺取法贪心的去找最合适的区间。

　　要注意的是尺取法时首尾指针一定不能相同，因为这时区间相减结果为0，但实际上区间为空，这是不存在的，可能会产生错误的结果。

　　处理时，把（0,0）这个点也放进数组一起排序，比单独判断起点为1的区间更方便。

　　还有ans初始化的值INF一定要大于t的最大值。

　　最后说说这个题最重要的突破口，对前缀和排序。为什么这么做是对的呢？

　　因为这题是取区间的和的绝对值，所以所以用sum[r]-sum[l] 和 sum[l]-sum[r]是没有区别的。

　　这样排序后，把原来无序的前缀和变成有序的了，就便于枚举的处理，并且不影响最终结果。

　　以上分析来自参考资料[1]。

AC代码：

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
#define P pair<int ,int >
const int maxn=1e5+10;

int n,k;
P p[maxn];

bool cmp(P _a,P _b){
    return _a.second < _b.second;
}
void Solve(int t)
{
    int l=0,r=1;
    int resL=p[l].first,resR=p[r].first;//先假设区间[1,p[1].first]为解
    int resSum=p[r].second-p[l].second;
    while(r <= n)
    {
        int curSum=p[r].second-p[l].second;
        if(abs(curSum-t) < abs(resSum-t))//判断是否可以更新 resSum
        {
            resSum=curSum;
            resL=p[l].first;
            resR=p[r].first;
        }
        if(curSum < t)//如果当前区间值过小,增大当前值
            r++;
        else if(curSum > t)//如果当前区间值过大,减小当前值
            l++;
        else
            break;
        if(l == r)
            r++;
    }
    if(resL > resR)
        swap(resL,resR);
    printf("%d %d %d
",resSum,resL+1,resR);//while()循环中做区间减法时始终左边界一直被减掉
}
int main()
{
//    freopen("C:\Users\lenovo\Desktop\in.txt\poj2566.txt","r",stdin);
    while(~scanf("%d%d",&n,&k),n != 0 || k != 0)
    {
        int sum=0;
        for(int i=1;i <= n;++i)
        {
            int val;
            scanf("%d",&val);
            sum += val;
            p[i]=P(i,sum);
        }
        p[0]=P(0,0);
        sort(p,p+n+1,cmp);
        while(k--)
        {
            int t;
            scanf("%d",&t);
            Solve(t);
        }
    }
    return 0;
}

我的理解：

　　为什么对前缀和用尺取法是正确的呢？

　　定义 pair<int ,int > 型变量 p[ maxn ];

　　p[ i ].first : 右边界;

　　p[ i ].second : 前 p[ i ].first 项和;

　　将 p 按前缀和从小到大排序后，如图所示：

　　

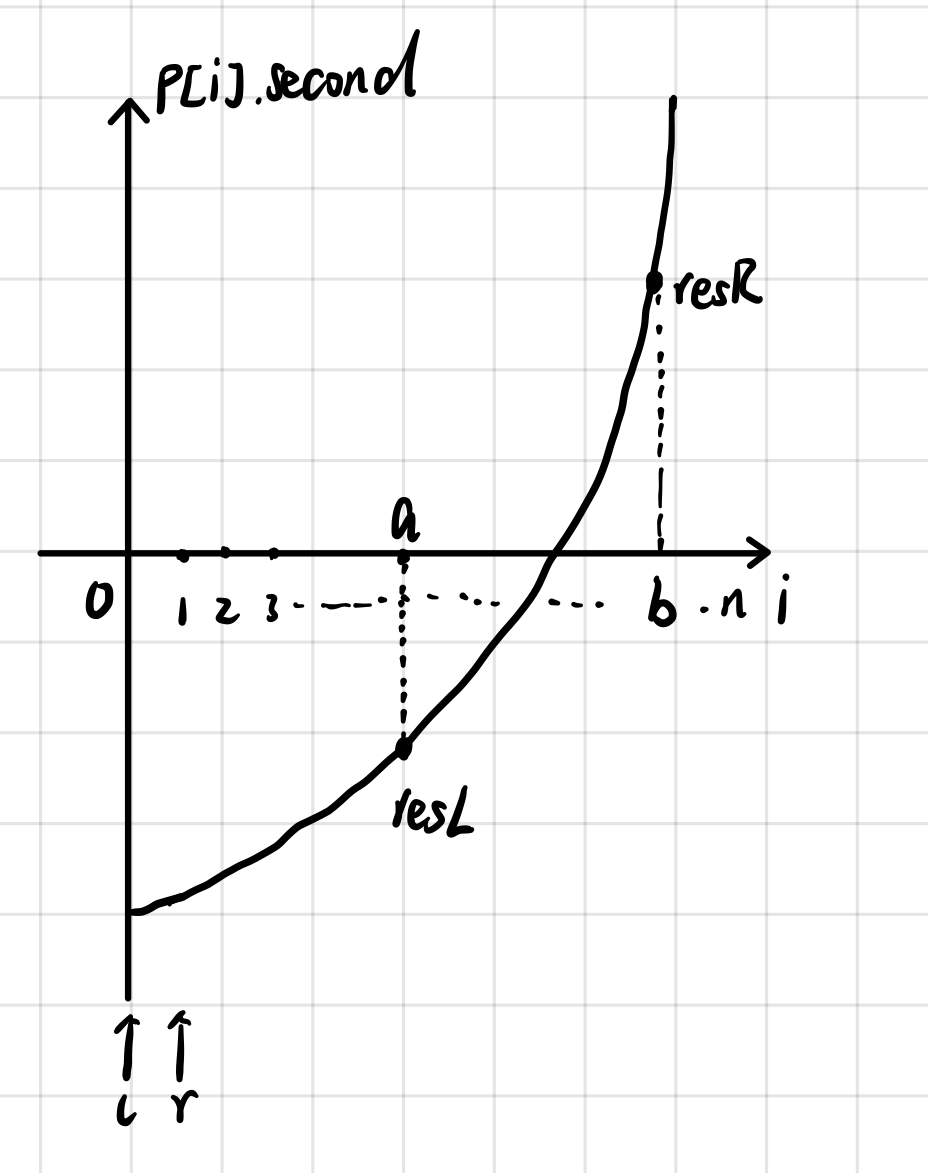
　　纵坐标 : 排序后的前缀和

　　假设 ( p[b].second-p[a].second ) 距 t 最近 , resSum = p[b].second-p[a].second;

　　问题1：当 R 来到区间(a,b)时，L 有可能超过 a 吗？

　　答案：不会。

　　分析如下：当 a < R < b , L = a 时, 令 curSum=p[R].second-p[L].second;

　　易得 curSum < resSum;

　　根据 Solve() 中 while() 循环的代码，只由当 curSum > target 时，才会使 L++；

　　假设 curSum > target , 则 resSum > curSum > target，那么答案就为 curSum 所标示的区间而不是resSum 所表示的区间，与假设不符;
　　故当 L = a , a < R < b 时，curSum < target ，直到 R 来到 b 。

　　问题2：当 L < a 时，R 有可能超过 b 吗？

　　答案：不会。

　　分析如下：当 L < a , R = b 时，令 curSum=p[R].second-p[L].second;

　　易得 curSum > resSum;

　　根据 Solve() 中 while() 循环的代码，只由当 curSum < target 时，才会使R++；

　　假设 curSum < target , 则 resSum < curSum < target，那么答案就为 curSum 所标示的区间而不是resSum 所表示的区间，与假设不符;

　　故当 R = b , L < a 时，curSum > target ，直到 L 来到 a 。

　　综上所述，L,R一定会来到答案所对应的区间。

　　问题3：为什么要加入 (0,0)点？

　　根据Solve()中的while()循环可知，curSum求的是L,R区间的差集（大-小）的和，如果答案的左区间为 1 呢？

　　不加入 (0,0) 点就永远也不可能使某两区间的差集（大-小）包含 1 .

　　或者说可以另用一重循环判断，感觉加入 (0,0)点更美观，哈哈哈。