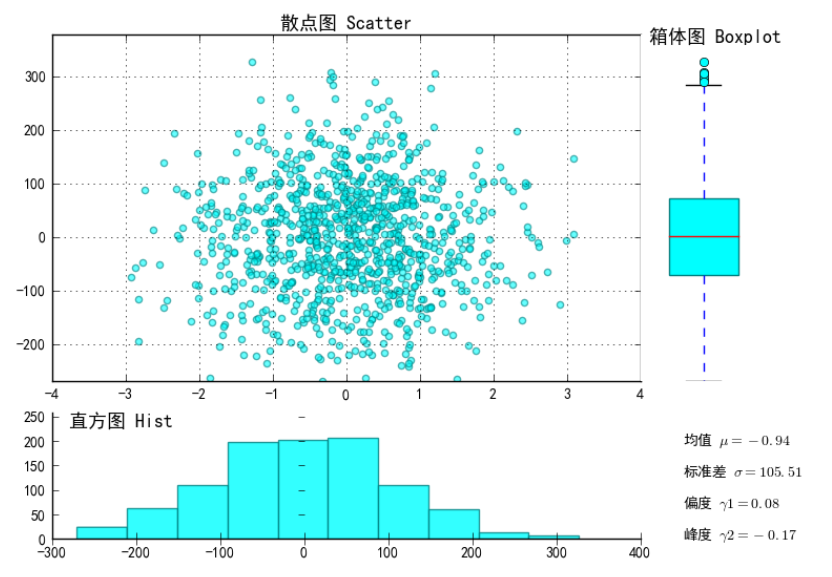
散点图进阶,结合箱体图与直方图对数据形成全面的认识
描述数据集中趋势的分析量:
均值 - 全部数据的算术平均值
众数 - 一组数据中出现次数最多的变量值
中位数 - 一组数据经过顺序排列后处于中间位置上的变量值
描述数据离散程度的分析量:
方差 - 一组数据各变量值与其平均值离差平方和的平均数
标准差 - 方差的平方根
偏态 - 描述数据分布形态的统计量,其描述的是某总体取值分布的对称性。偏度 = 三阶中心距 / 标准差的三次方
峰度 - 描述总体中所有取值分布形态陡缓程度的统计量,这个统计量需要与正态分布相比较。 峰度 = 四阶中心距 / 方差平方(标准差四次方) - 3
描述性分析数据的计算:

1 # 准备数据 2 import numpy as np 3 import matplotlib.pyplot as plt 4 5 n = 1000 6 x = np.random.randn(n) 7 y = [int((item)*100) for item in np.random.randn( n )] #100以内的正整数随机数 8 9 # 均值μ 10 mu = np.mean(y) 11 # 标准差δ sigma = np.sqrt(np.sum(np.square( y - mu ))/n) 12 sigma = np.std(y) 13 # 峰度(公式准确度待确认) 14 kurtosis = np.sum(np.power((y - mu),4))/(n) # 四阶中心距 15 kurtosis = kurtosis / np.power(sigma,4)-3 # 峰度 = 四阶中心距 / 方差平方(标准差四次方) - 3 16 # 偏度 17 skewness = np.sum(np.power((y - mu),3))/(n) # 三阶中心距 18 skewness = skewness / np.power(sigma,3) # 偏度 = 三阶中心距 / 标准差的三次方 19 20 print(mu, sigma,skewness, kurtosis)
结果:
-0.944 105.50647783 0.0750892544722 -0.171492308767
图表显示

1 # 图表显示 2 fig = plt.figure( figsize = ( 8, 6 )) # 设置图表大小 3 #设置图表的大小:[左, 下, 宽, 高] 规定的矩形区域 (全部是0~1之间的数,表示比例) 4 rect_1 = [0.15, 0.30, 0.7, 0.55] 5 rect_2 = [0.85, 0.30, 0.15, 0.55] 6 rect_3 = [0.15, 0.05, 0.7, 0.2] 7 fig_1 = plt.axes(rect_1) # 第一个图表 8 fig_2 = plt.axes(rect_2) # 第二个图表 9 fig_3 = plt.axes(rect_3) # 第三个图表 10 #设置图表公共变量 11 title_size = 13 12 inner_color = 'cyan' 13 outer_color = 'teal' 14 # 第一个图表:散点图 15 fig_1.scatter( x, y, s = 20, color = inner_color, edgecolor = outer_color, alpha = 0.6) 16 fig_1.set_title('散点图 Scatter', fontsize = title_size) 17 fig_1.set_ylim( min(y),max(y)+50 ) 18 fig_1.grid(True) 19 20 # 第二个图表:箱体图 21 fig_2.boxplot(y, 22 widths = 0.55, 23 patch_artist = True, # 要求用自定义颜色填充盒形图,默认白色填充 24 boxprops = {'color':outer_color,'facecolor':inner_color, }, # 设置箱体属性,填充色和边框色 25 flierprops = {'marker':'o','markerfacecolor':inner_color,'color':outer_color,}, # 设置异常值属性,点的形状、填充色和边框色 26 meanprops = {'marker':'h','markerfacecolor':outer_color}, # 设置均值点的属性,点的形状、填充色 27 medianprops = {'linestyle':'-','color':'red'} # 设置中位数线的属性,线的类型和颜色 28 ) 29 fig_2.set_ylim( fig_1.get_ylim()) #设置箱体图与散点图同一纵坐标轴 30 fig_2.get_yaxis().set_visible(False) #关闭坐标轴 31 fig_2.get_xaxis().set_visible(False) #关闭坐标轴 32 # 去除边框显示 33 remove_col = ['top','bottom','left','right'] 34 for item in remove_col: 35 fig_2.spines[item].set_visible(False) 36 fig_2.spines[item].set_position(('data',0)) 37 fig.text(0.86, 0.84,'箱体图 Boxplot', fontsize = title_size ) 38 39 # 第三个图表:直方图 40 n, bins, patches = fig_3.hist( y, color = inner_color, alpha = 0.8, edgecolor = outer_color ) 41 fig_3.set_ylim([0,max(n)+50]) 42 fig_3.spines['top'].set_visible(False) # 去除边框显示 43 fig_3.spines['top'].set_position(('data',0)) # 去除边框刻度显示 44 fig_3.spines['right'].set_color('none') # 去除边框显示 45 fig_3.spines['right'].set_position(('data',0)) # 去除边框刻度显示 46 fig.text(0.17, 0.23,'直方图 Hist', fontsize = title_size ) 47 48 # 文本信息 49 fig.text(0.9, .20, '均值 $mu = {0:.2f}$'.format(mu)) 50 fig.text(0.9, .15, '标准差 $sigma = {0:.2f}$'.format(sigma)) 51 fig.text(0.9, .10, '偏度 $gamma 1 = {0:.2f}$'.format(skewness)) 52 fig.text(0.9, .05, '峰度 $gamma 2 = {0:.2f}$'.format(kurtosis)) 53 plt.show()
结果: