1.python内置数据结构性能分析
- list

下面来看看四段创建列表代码,比较一下各段代码的效率:
def test1(): l = [] for i in range(1000): l = l + [i] def test2(): l = [] for i in range(1000): l.append(i) def test3(): l = [i for i in range(1000)] def test4(): l = list(range(1000)) from timeit import Timer t1 = Timer("test1()", "from __main__ import test1") print("concat ",t1.timeit(number=1000), "milliseconds") t2 = Timer("test2()", "from __main__ import test2") print("append ",t2.timeit(number=1000), "milliseconds") t3 = Timer("test3()", "from __main__ import test3") print("comprehension ",t3.timeit(number=1000), "milliseconds") t4 = Timer("test4()", "from __main__ import test4") print("list range ",t4.timeit(number=1000), "milliseconds") #------------------------------------------------ # 输出如下: concat 2.13730173426522 milliseconds append 0.11433030026869506 milliseconds comprehension 0.04344365808379402 milliseconds list range 0.017494041710804265 milliseconds
再来看看Pop操作:
x = list(range(2000000)) pop_zero = Timer("x.pop(0)","from __main__ import x") print("pop_zero ",pop_zero.timeit(number=1000), "milliseconds") x = list(range(2000000)) pop_end = Timer("x.pop()","from __main__ import x") print("pop_end ",pop_end.timeit(number=1000), "milliseconds") #-------------------------------------------- pop_zero 2.025613480337966 milliseconds pop_end 0.00012786854258539648 milliseconds
再来看看append与insert差异:
from timeit import Timer x = list(range(2000000)) insert_first = Timer("x.insert(0,-1)","from __main__ import x") print("insert_first ",insert_first.timeit(number=1000), "milliseconds") x = list(range(2000000)) append_end = Timer("x.append(-1)","from __main__ import x") print("append_end ",append_end.timeit(number=1000), "milliseconds") #------------------输出结果 insert_first 2.099321355885524 milliseconds append_end 9.493918546477076e-05 milliseconds
总结,Python的list的实现不是类似数据结构中的单链表,而是类似数组,也就是说list中的元素保存在一片连续的内存区域中,这样的话只有知道元素索引就能确定元素的内存位置,从而直接取出该位置上的值,但是它的缺点在于前插需要移动元素,而且随着list中元素的增多需要移动的元素也就越多,花费的时间也就自然多了。而单链表不同,单链表要得到某个位置上的元素必须要从头开始遍历,但是它的插入操作(前插或者后插)基本上都是恒定的时间,与链表中元素的多少没有关系,因为元素之间用“指针”维护着他们的关系。
- dict

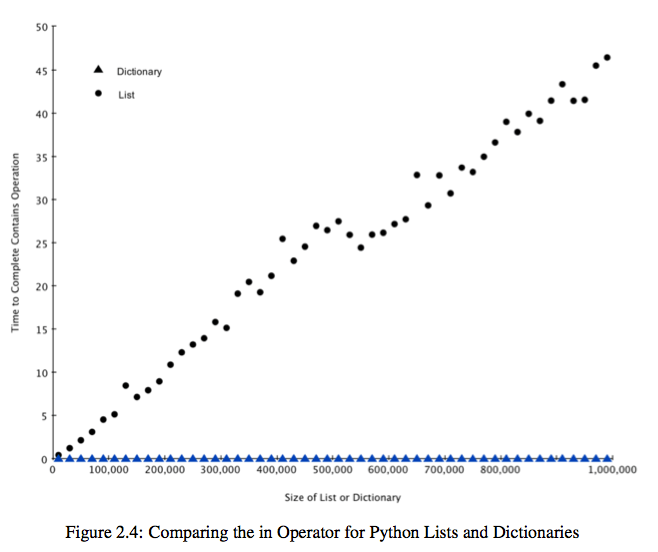
Dictionary和List的性能比较:list基本上随着其元素的数目呈线性增长,而dictionary一直维持在很短很短的时间内。Dictionary类似Java中的HashMap,内部实现使用了前面提到的hash函数,所以查找和删除都是常数时间的。
import timeit import random for i in range(10000,1000001,20000): t = timeit.Timer("random.randrange(%d) in x"%i,"from __main__ import random,x") x = list(range(i)) lst_time = t.timeit(number=1000) x = {j:None for j in range(i)} d_time = t.timeit(number=1000) print("%d,%10.3f,%10.3f" % (i, lst_time, d_time))
其输出结果如下图:
- 栈---先进后出
class Stack: def __init__(self): self.items = [] def is_empty(self): return self.items == [] def push(self, item): self.items.append(item) def pop(self): return self.items.pop() def peek(self): return self.items[len(self.items)-1] def size(self): return len(self.items) s = Stack() print(s.is_empty()) s.push(4) s.push('dog') print(s.peek()) s.push(True) print(s.size()) print(s.is_empty()) s.push(8.4) print(s.pop()) print(s.pop()) print(s.size())
- 队列---先进先出
class Queue: def __init__(self): self.items = [] def is_empty(self): return self.items == [] def enqueue(self, item): self.items.insert(0,item) def dequeue(self): return self.items.pop() def size(self): return len(self.items) q = Queue() q.enqueue('hello') q.enqueue('dog') print(q.items) q.enqueue(3) q.dequeue() print(q.items)
- 双向队列---两边都可以进,也都可以出
class Deque: def __init__(self): self.items = [] def is_empty(self): return self.items == [] def add_front(self, item): self.items.append(item) def add_rear(self, item): self.items.insert(0,item) def remove_front(self): return self.items.pop() def remove_rear(self): return self.items.pop(0) def size(self): return len(self.items) dq=Deque(); dq.add_front('dog'); dq.add_rear('cat'); print(dq.items) dq.remove_front(); dq.add_front('pig'); print(dq.items)
- 二叉树
一个节点最多有两个孩子节点的树。如果是从0索引开始存储,那么对应于节点p的孩子节点是2p+1和2p+2两个节点,相反,节点p的父亲节点是(p-1)/2位置上的点
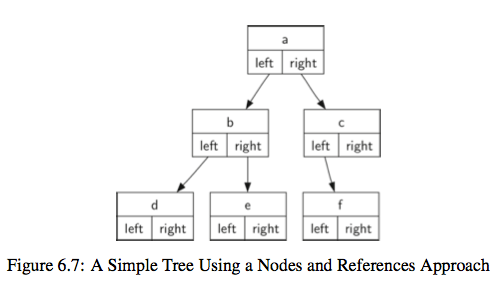
class BinaryTree: def __init__(self,root): self.key = root self.left_child = None self.right_child = None def insert_left(self,new_node): if self.left_child == None: self.left_child = BinaryTree(new_node) else: t = BinaryTree(new_node) t.left_child = self.left_child self.left_child = t def insert_right(self,new_node): if self.right_child == None: self.right_child = BinaryTree(new_node) else: t = BinaryTree(new_node) t.right_child = self.right_child self.right_child = t def get_right_child(self): return self.right_child def get_left_child(self): return self.left_child def set_root_val(self,obj): self.key = obj def get_root_val(self): return self.key r = BinaryTree('a') print(r.get_root_val()) r.insert_left('b') print(r.get_left_child().get_root_val()) # 获取'b'的值 r.set_root_val('hello world') # 修改根节点的值 print(r.get_root_val())