Codeforces Round #484 (Div. 2) E. Billiard

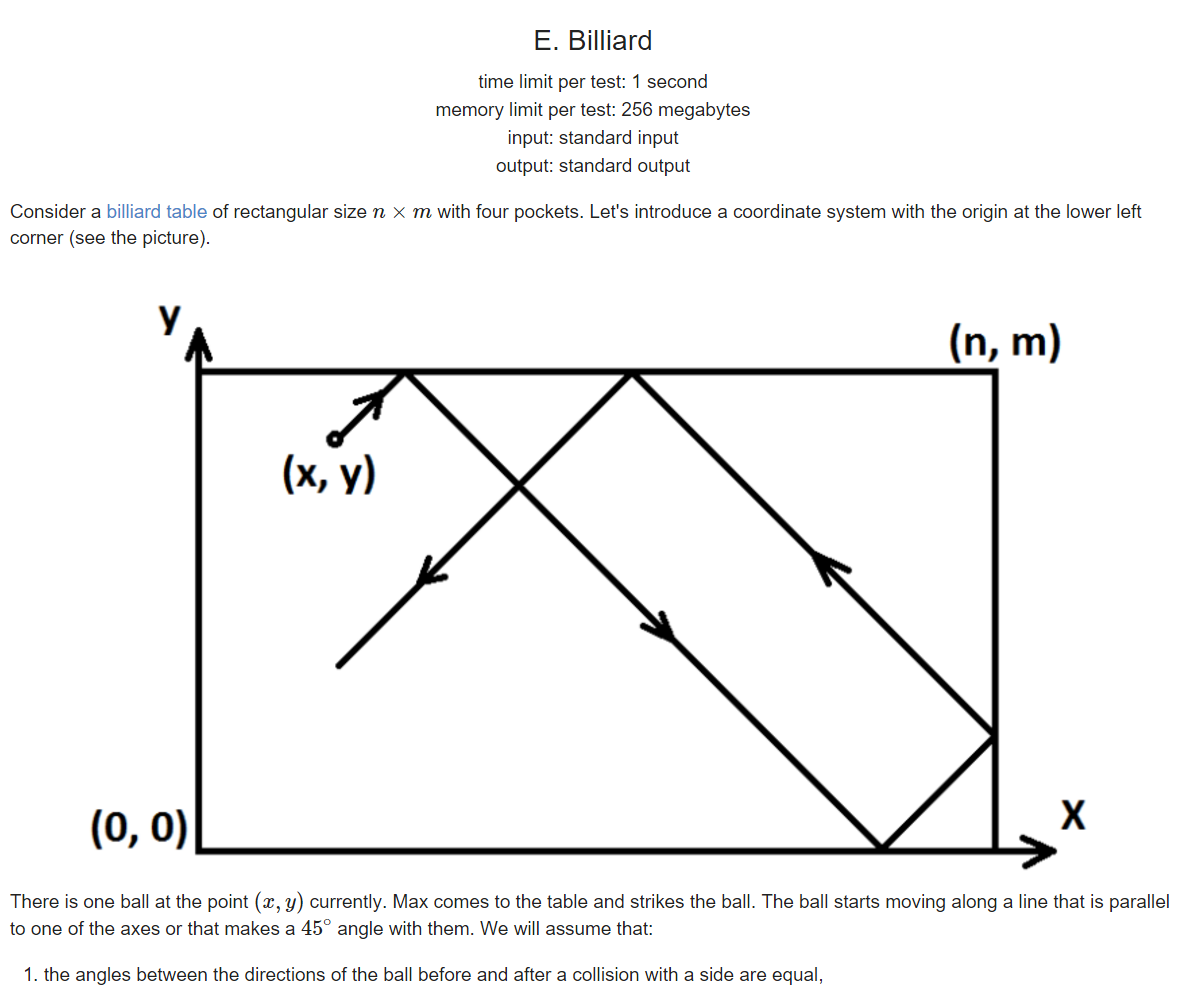
题目大意：

有一个方形区域，四个角各有一个口袋，在（x,y）出有一小球，以Vx,Vy速度击出，碰到边界会像光路一样反
弹，问最先掉到哪个口袋里

　　

分析：

其实问题的关键在于将反射线段利用光路的性质转换成一条直线，如下图

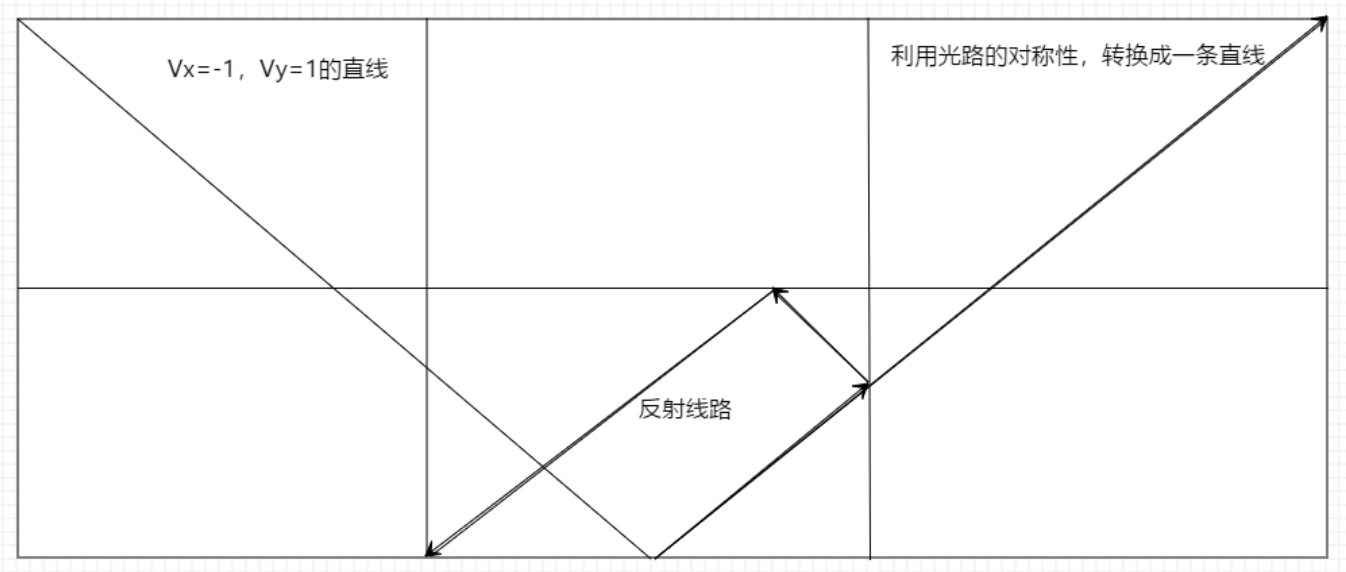
同时斜率为-1的情况实际上与斜率为1的直线第一次经过的顶点时对称的，所以为了方便起见，我们将直线都转换成斜率为1的直线，即如果输入的Vx=-1，我们需要将x=n-x(Vy=-1同理y=m-y),同时还能得到an+bm=c,进一步可以得到an+bm=x-y，最后就是用扩欧了，如果(x-y)%gcd(a,b)!=0输出-1,否则就用扩欧求得答案。
扩欧存在解时的讨论：如果a，b的个数为奇数，则通过的是(n,m)；都为偶数时，则通过的是(0,0)；a为奇，b为偶，则通过（n,0)；a为偶，b为奇，则通过(0,m)。由此我们需要先求出a,b的奇偶性。这里我们要注意下，因为必定是需要第一块的，而且不一定在第一块里面就碰到顶点，所以在对a取模的时候应该_a=(a%_m+m-1)%m+1,将第一块先减去，最后再加回来。b可以直接根据a算出来，_b=-(x-y+_a*n)/m,在判断_a,_b的是奇数还是偶数。最后需要注意下，如果原本直线斜率为-1,扩欧得到的答案是对称过的点，我们还需要对称回去的，详细看代码

code:

#define debug
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int>PII;
const int maxn=1e5;
const int INF=0x3f3f3f3f;
const int inf=0x7fffffff;
const int mod=1e9+7;
const int MOD=10007;
//----
//define
int n,m,x,y,vx,vy;
//exgcd
ll exgcd(int a,int b,ll &x,ll &y) {
	if(b==0) {
		x=1;
		y=0;
		return a;
	} else {
		ll tmp=exgcd(b,a%b,y,x);
		y-=(a/b)*x;
		return tmp;
	}
}
//gcd
ll gcd(ll a,ll b) {
	return b==0?a:gcd(b,a%b);
}
//solve
void solve() {
	while(cin>>n>>m>>x>>y>>vx>>vy) {
		//vx=0,vy=0的这两种情况可以直接判断掉 
		if(!vx) {
			if(x==0||x==n) {
				if(vy>0)cout<<x<<" "<<m<<endl;
				else cout<<x<<" "<<0<<endl;
			} else {
				cout<<-1<<endl;
			}
			continue;
		}
		if(!vy) {
			if(y==0||y==m) {
				if(vx>0)cout<<n<<" "<<y<<endl;
				else cout<<0<<" "<<y<<endl;
			} else {
				cout<<-1<<endl;
			}
			continue;
		}
		//---------------------------------------- 
		int rx=0,ry=0;
		ll a,b,d=exgcd(n,m,a,b);
		//关于x=y轴对称 
		if(vx==-1){
			rx=1;
			x=n-x;
		} 
		//关于y=x轴对称 
		if(vy==-1){
			ry=1;
			y=m-y;
		}
		ll k=x-y;
		//无解的情况 
		if(k%d){
			cout<<-1<<endl;
			continue;
		}
		k/=d;
		a*=k;b*=k;
		ll _n=n/d,_m=m/d;
		ll _a=(a%_m+_m-1)%_m+1,_b=-((x-y)-_a*n)/m;
		ll ansx=n,ansy=m;
		if(a%2==0)ansx=n-ansx;
		if(_b%2==0)ansy=m-ansy;
		if(rx)ansx=n-ansx;
		if(ry)ansy=m-ansy;
		cout<<ansx<<" "<<ansy<<endl;
	}
}

int main() {
	ios_base::sync_with_stdio(0);
#ifdef debug
	freopen("in.txt","r",stdin);
//	freopen("out.txt","w",stdout);
#endif
	cin.tie(0);
	cout.tie(0);
	solve();
	return 0;
}