机器学习：多元线性回归

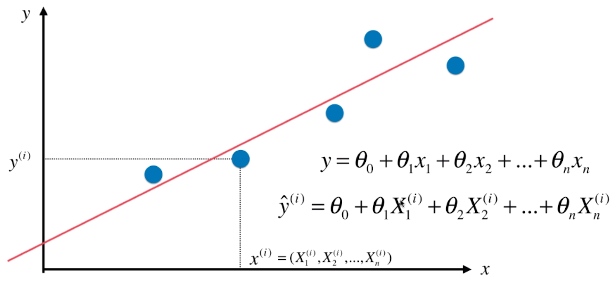
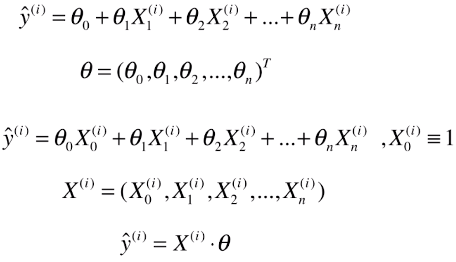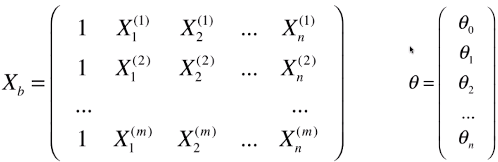一、多元线性回归基础

• 简单线性回归算法只有一个特征值（x），通常线性回归算法中有多个特征值，有的甚至有成千上万个特征值；
• 多元线性回归中有多种特征，每一种特征都与 y 呈线性关系，只是线性关系的系数不同；
• 多元线性回归的模型可以解决一元线性回归问题；
• 多元线性回归模型中，每一种特征都与值（也就是 y）呈线性关系，从 θ₁ 到 θ_n ，以此为第一个特征到第 n 个特征与值的线性关系系数，θ₁ 是第一个特征（X 中的第一列）的系数。

　1）多元线性回归问题的解决思路

• 求解思路与简单线性回归的思路一样
• yⁱ = θ₀ + θ₁X_1ⁱ + θ₂X_2ⁱ + θ₃X_3ⁱ + ... + θ_nX_{nⁱ：第 i 个样本对应的预测值；}
  

1. X = array([X¹, X², X³ , ..., X^m])^T：数据集，m 个样本，m 行 n 列个数据；
2. Xⁱ：数据集中的第 i 个向量，也是该数据集中的第 i 个样本；
3. Xⁱ = array([x₁, x₂, x₃,  ... , x_n])
4. x_n：每一行（一个样本）的一个元素（特征值）

• 

• 

　2）多元线性回归的公式推导

　　A）原始公式

• 

1. θ：参数向量，必须为列向量，才能与数据集矩阵X相乘：X*θ，得到的也是一个列向量
2. ý⁽ⁱ⁾：模型的预测值
3. X⁽ⁱ⁾：变形后的一个样本，也是变形后的数据集矩阵的第 i 行
4. X₀⁽ⁱ⁾：第 i 行的第0号元素；  #  原因：为了让计算式的每一项的格式统一，并且和θ₀结合在一起，方便整个公式的推导，虚构为X⁽ⁱ⁾的第0个特征；
5. X₀⁽ⁱ⁾ ≡ 1：此元素恒等于1，变形后的公式与原公式一样

　　B）变形数据集矩阵

• 

1. 新的数据集矩阵：X_b，比原矩阵X多了一列：X₀，全部为1
2. 变形后的数学模型：ý = X_b * θ
3. ý为列向量，每一个元素（ý⁽ⁱ⁾）为每一个样本X⁽ⁱ⁾讲过预测后得到的预测值
4. 矩阵相乘有先后，不能写成θ * X_b

　　C）优化目标函数

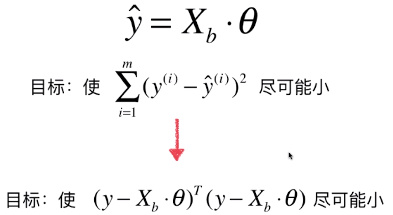
1. 数学推导（对矩阵求导（非本科学校内容））：得到θ的表达式
2. 目标函数中的X_b：有X_test变形而来
3. 预测时，X_b的列数（也就是特征种类）与θ中的元素个数相等

• 最终的参数表达式：

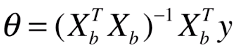
1. 此公式为多元线性回归的正规方程解（Normal Equation）
2. 公式缺点：时间复杂度高：O(n³)，即使通过手段优化后：O(n^2.4) ，效率低；
3. 优点：不需要对数据做归一化处理；  # 因为数据集中的数据直接参数运算；
4. X_b：有X_train变形而来
5. (X_b^TX_b)^-1：其中 -1 表示矩阵的逆矩阵
6. 逆矩阵：AB = BA = E，矩阵A、B均为方阵，E为单位矩阵
7. 方阵：n x n 的矩阵；
8. 单位矩阵：一个对角为1，E[0, 0] = E[1, 1] = E[2, 2] = ... = E[n, n] = 1，其余元素为0；

二、实现多元线性回归

　　

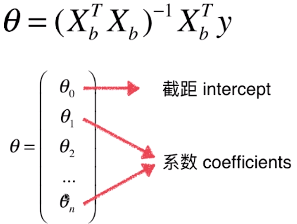
1. θ中有 n + 1 个数值，实际样本中只有 n 个维度
2. θ₀是截距（intercept），θ₁ ~ θ_n是系数（coefficients）

• 一般对用户做汇报时，不是直接汇报θ，而是将θ分开为截距、系数两部分

1. 分开汇报的原因：系数部分中的每一个θ值，都对应着原来样本中的一个特征，某种程度上，系数中的一个θ值可以用来描述特征对于最终样本的确定做的贡献程度，θ₀和特征没有关系，只是一个偏移；

　1）自己的算法实现

• 具体代码

  import numpy as np
  from sklearn.metrics import r2_score
  
  class LinearRegression:
  
      def __init__(self):
          """初始化Linear Regression模型"""
          # coef_：截距
          # interception：系数
          # _theta：θ，为私有变量
          # 私有变量：变量名首字母为一个"_"
          # 私有函数：函数名首字母为两个"_"
          self.coef_ = None
          self.interception_ = None
          self._theta = None
  
      def fit_normal(self, X_train, y_train):
          """根据孙连数据集X_train, y_train训练Linear Regression模型"""
          # fit的过程也是调参的过程，计算出参数θ，得到Linear Regression模型
          assert X_train.shape[0] == y_train.shape[0], 
              "the size of X_train must be equal to the size of y_train"
  
          # np.ones((m, n)):创建一个m行n列的全部为1的矩阵；(m, n)必须为tuple格式
          # np.hstack([array1, array2])：将两个矩阵在行的方向相加，增加列数，两个矩阵放在[]内
          X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
          self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)
  
          self.interception_ = self._theta[0]
          self.coef_ = self._theta[1:]
  
          return self
  
      def predict(self, X_predict):
          """给定待预测数据集X_predict, 返回表示X_predict的结果向量"""
          assert self.interception_ is not None and self.coef_ is not None, 
              "must fit before predict"
          assert X_predict.shape[1] == len(self.coef_), 
              "the feature number of X_predict must be equal to X_train"
  
          # 此处的X_b有预测数据集X_predict变形而来
          X_b = np.hstack([np.ones((X_predict.shape[0], 1)), X_predict])
          return X_b.dot(self._theta)
  
      def score(self, X_test, y_test):
          """根据训练数据集 X_test 和 y_test 确定当前模型的准确度"""
  
          y_predict = self.predict(X_test)
          return r2_score(y_test, y_predict)
  
      def __repr__(self):
          return "LinearRegression()"

• 在Jupyter NoteBook中使用自己的代码

  import numpy as np
  import matplotlib.pyplot as plt
  from sklearn import datasets
  
  boston = datasets.load_boston()
  
  X = boston.data
  y = boston.target
  
  # 取结果小于50的数据
  X = X[y < 50.0]
  y = y[y < 50.0]
  
  # 1）分割原始数据
  from ALG.data_split import train_test_split
  
  X_train, X_test, y_train, y_test = train_test_split(X, y, seed=666)
  
  
  # 2）导入-实例化-fit自己的算法
  from LR.L_R import LinearRegression
  
  reg = LinearRegression()
  reg.fit_normal(X_train, y_train)
  
  # 3）预测
  # 得到准确度
  reg.score(X_test, y_test)
  # 输出：0.8129802602658466

　2）调用scikit-learn中的算法

•  使用线性回归算法

  # 导入 - 实例化 - fit
  from skleaen.linear_model import LinearRegression
  
  lin_reg = LinearRegression()
  lin_reg.fit(X_train, y_train)
  
  # 查看截距
  lin_reg.interception_
  
  # 查看系数
  in_reg.coef_
  
  # 查看模型预测准确度
  lin_reg.score(X_test, y_test)
  # 输出：0.8129802602658476

• 使用kNN Regressor的算法KneighborsRegressor()

1. 只使用默认参数k == 5

   from sklearn.neighbors import KNeighborsRegressor
   
   knn_reg = KNeighborsRegressor()
   knn_reg.fit(X_train, y_train)
   knn_reg.score(X_test, y_test)
   # 输出：0.5865412198300899

2. 对KNeighborsRegressor进行调参（网格搜索）：

   使用GridSearchCV下的best_score_参数，获取网格搜索后的模型的准确度

   from sklearn.model_selection import GridSearchCV
   
   param_grid = [
       {
           "weights": ["uniform"],
           "n_neighbors": [i for i in range(1, 11)]
       },
       {
           "weights": ["distance"],
           "n_neighbors": [i for i in range(1, 11)],
           "p": [i for i in range(1, 6)]
       }    
   ]
   
   knn_reg = KNeighborsRegressor()
   
   # grid_search是一个网格搜索(GridSearchCV)的对象，fit之后才会确认最佳模型及其参数
   grid_search = GridSearchCV(knn_reg, param_grid, n_jobs=-1, verbose=1)
   grid_search.fit(X_train, y_train)
   
   # 查看最佳的取值结果
   grid_search.best_params_
   # 输出：{'n_neighbors': 5, 'p': 1, 'weights': 'distance'}
   
   # 使用GridSearchCV下的best_score_参数，获取网格搜索后的模型的准确度
   grid_search.best_score_
   # 输出：0.634093080186858

3. 对kNeighborsRegressor进行调参（网格搜索）：

   调用最优模型的score()函数（也就是KNeighborsRegressor()算法的score()函数），获取足有算法模型的准确度

   # 获取网格搜索后的最优的KNeighborsRegressor()算法的模型
   grid_search.best_estimator_
   # 输出：KNeighborsRegressor(algorithm='auto', leaf_size=30, metric='minkowski',
             metric_params=None, n_jobs=1, n_neighbors=5, p=1,
             weights='distance')
   
   # 调用最优模型的score()函数，获取足有算法模型的准确度
   grid_search.best_estimator_.score(X_test, y_test)
   # 输出：0.7044357727037996

　3）总结

• 关于网格化搜索，参考：机器学习：使用scikit-learn库中的网格搜索调参
• kNN算法解决问题的步骤：

1. 获取原始数据
2. 数据分割
3. 数据归一化
4. 导入、实例化算法
5. 网格搜索：设置参数范围——实例化GridSearchCV()——fit
6. 获取准确度：grid_search.best_score_、grid_search.best_estimator_.score(X_test, y_test)； # grid_search，GridSearchCV()的实例对象
7. grid_search.best_score_：使用GridSearchCV()的best_score_参数，查看最佳模型的准确度；
8. grid_search.best_estimator_：返回最佳模型，也就是算法KNeighborsRegressor()的模型；
9. grid_search.best_estimator_.score(X_test, y_test)：调用算法KNeighborsRegressor()的score()函数，获取最佳模型的准确度

• scikit-learn中的LinearRegression算法与自己的算法得到的结果略有不同，因为scikit-learn中对原始数据集分割时，随机序列（对index乱序后分割）的生成上是不同的，导致生成的训练、测试数据集不同

• kNN算法中，最佳模型和参数，是根据对比GridSearchCV()内部的逻辑运算（best_score_）所得到的准确度而确定的，不是kNN算法（KNeighborsClassifier()、KneighborsRegressor()等）中的score()函数；两种方式的内部逻辑是不同的；

• 使用机器学习算法解决问题时，会用不同的算法得到不同的准确度，比较算法优劣时，不能很武断的做判断，要细心考虑不同算法对准确度计算方式，因为同一个算法通过不同的方式可以得到不同的准确度：grid_search.best_score_、grid_search.best_estimator_.score(X_test, y_test)，同一个算法模型，使用不同的方式得出的准确度不同。