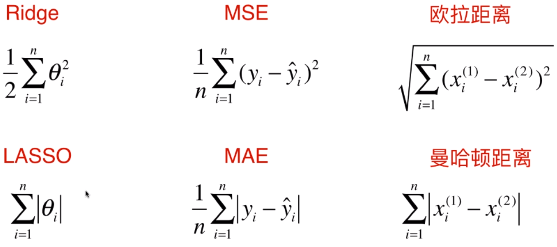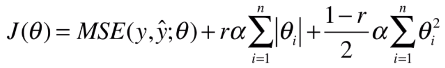一、岭回归和 LASSO 回归的推导过程
1)岭回归和LASSO回归都是解决模型训练过程中的过拟合问题
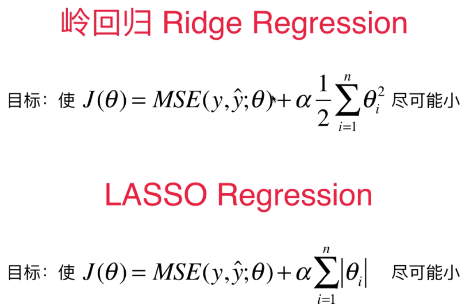
- 具体操作:在原始的损失函数后添加正则项,来尽量的减小模型学习到的 θ 的大小,使得模型的泛化能力更强;
2)比较 Ridge 和 LASSO
- 名词
-
Ridge、LASSO:衡量模型正则化;
-
MSE、MAE:衡量回归结果的好坏;
-
欧拉距离、曼哈顿距离:衡量两点之间距离的大小;
- 理解
- Ridge、LASSO:在损失函数后添加的正则项不同;
- MSE、MAE:两种误差的表现形式与对应的 Ridge 和 LASSO 的两种正则项的形式很像;
- 欧拉距离、曼哈顿距离:欧拉距离和曼哈顿距离的整体表现形式,与 Ridge、LASSO 两种正则项的形式也很像;
-
其它
- 在机器学习领域,对于不同的应用会有不同的名词来表达不同的衡量标准,但其背后本质的数学思想非常相近,表达出的数学的含义也近乎一致,只不过应用在了不同的场景中而产生了不同的效果,进而生成了不同的名词;
3)明科夫斯基距离
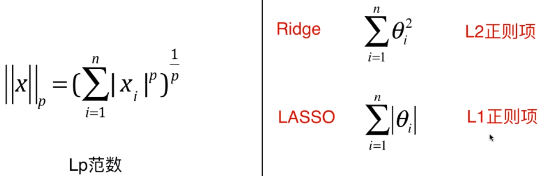
- 明科夫斯基距离:
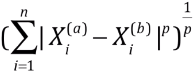
- 将明科夫斯基距离泛化:Lp 范数
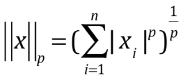
- p = 1:称为 L1 范数,相当于从 (0, 0) 点到 X 向量的曼哈顿距离;
- p = 2:称为 L2 范数,相当于从 (0, 0) 点到 X 向量的欧拉距离;
4)L1 正则、L2 正则
- Ridge 回归中添加了 L2 正则项,LASSO 回归中添加了 L1 正则项;
- L2 正则项和 L2 范数的区别在于,L2 正则项没有开平方,但有时候也直接称 L2 正则项为 L2 范数;(同理 L1 范数与 L1 正则项的关系)
- 原因: L2 正则项是用于放在损失函数中进行最优化,如果将 L2 正则项加上开根号,不会影响损失函数优化的最终结果,但是不带根号会显得整个式子更加简单,所以对于 L2 正则项的式子中不带根号;
- 同理在数学理论上也存在 Ln 正则项;
5)L0 正则
- 目的:使 θ 的个数尽量少,进而限制 θ,使得拟合曲线上下抖动幅度不要太大,模型的泛化能力也会得以提高;
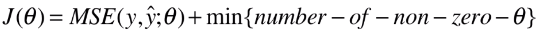
- L0 的正则项:描述非 0 的 θ 参数的个数;
- 实际中很少使用 L0 正则来进行模型正则化的过程,而是用 L1 正则代替;
- 原因: L0 正则的优化是一个 NP 难的问题;它不能使用诸如梯度下降法,甚至是直接求出一个数学公式这样的方式来直接找到最优解; L0 正则项本质是一个离散最优化的问题,可能需要穷举所有的让各种 θ 的组合为 0 的可能情况,然后依次来计算 J(θ) ,进而来觉得让哪些 θ 为 0 哪些 θ 不为 0,所以说 L0 正则的优化是一个 NP 难的问题;
- 如果想限制 θ 的个数,通常使用 L1 正则;
二、弹性网(Elastic Net)
1)公式
- 功能:也是解决模型训练过程中的过拟合问题;
- 操作:在损失函数后添加 L1 正则项和 L2 正则项;
- 特点:同时结合了 岭回归和 LASSO 回归的优势;
- r:新的超参数,表示添加的两个正则项的比例(分别为 r、1-r );
2)现实中,在进行正则化的过程中,通常要先使用 岭回归
- 优点:岭回归计算更精准;
- 缺点:不具有特征选择的功能;
- 原因:如果特征非常多的话,岭回归不能将某些 θ 设置为 0,若 θ 的量太大的话到导致整体计算量也非常的大;
3)当特征非常多时,应先考虑使用 弹性网
- 原因:弹性网结合了岭回归的计算的优点,同时又结合了 LASSO 回归特征选择的优势;
三、总结与开拓
1)总结
- 训练的机器学习模型不是为了在训练数据集上有好的测试结果,而是希望在未来面对未知的数据集上有非常好的结果;
- 模型在面对未知数据集表现的能力,为该模型的泛化能力;(模型泛化是机器学习领域非常非常重要的话题)
- 分析和提升模型泛化能力的方法:
- 看学习曲线;
- 对模型进行交叉验证;
- 对模型进行正则化;
2)开拓
- LASSO 回归的缺点:急于将某些 θ 化为 0,过程中可能会产生一些错误,使得最终的模型的偏差比较大;
- 问题:LASSO 回归在模型优化的过程中是有选择的将某些 θ 化为 0 吗?或者说有没有什么条件使得尽量避免让相关性比较强的特征的系数化为 0 ?还是说这一行为只是单纯的数学运算,就为目标函数尽量达到目标状态?
- “可能产生的错误”:将一些相关性比较强的特征的参数 θ 也化为 0,导致该特征丢失;
- 开拓思路
- 弹性网结合了岭回归和 LASSO 回归二者的优势,小批量梯度下降法结合了批量梯度下降法和随机批量梯度下降法二者的优势,类似的方法在机器学习领域经常被运用,用来创造出新的方法。
- 打个比方理解机器学习
- 参加考试前要做很多练习题,练习题就相当于训练数据,目的不是为了在做练习题的过程中达到满分,而是通过做练习题让我们在面对新的考试题时得到更高的分数,考试中面对的新的题目相当于模型在未来生成环境中见到的新的数据。