一、基础理解
1)简介
- SVM(Support Vector Machine):支撑向量机,既可以解决分类问题,又可以解决回归问题;
- SVM 算法可分为:Hard Margin SVM、Soft Margin SVM,其中 Soft Margin SVM 算法是由 Hard Margin SVM 改进而来;
2)不适定问题
- 不适定问题:决策边界不唯一,可能会偏向某一样本类型,模型泛化能力较差;
- 具有不适定问题的模型的特点:决策边界不准确,泛化能力较差;
- 原因:模型由训练数据集训练所得,训练数据集并没有包含所有类型的所有样本,训练数据集的样本的分布,可能不能准确的反应不同类型的样本分布的真正规律,由训练数据集得到模型,该模型的决策边界也很可能不是真正的分类边界;这样的话,该模型的决策边界会偏向某一样本类型,使模型泛化能力较差。
3)逻辑回归中的 不适定问题
- 逻辑回归思想:定义一个概率函数,根据概率函数进行建模,形成损失函数,最小化损失函数得到决策边界;
- 决策边界可能是多种情况:
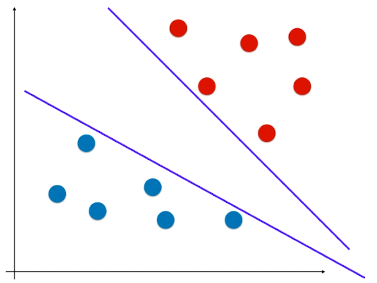
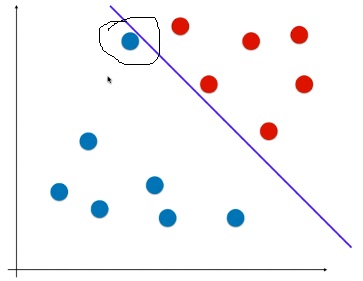
- 如图:如果有一个样本,离红色类型较近,离蓝色类型较远,但由于决策边界偏向红色类型,模型会判断该样本为蓝色类型:
4)SVM 算法的思想
- 解决“不适定问题”;
- 目的:找到一个最优决策边界,不仅很好的划分训练数据集,又有很好的泛化能力;
- 方法:让该决策边界离两种类别的样本都尽可能的远;
- 或者说,在逻辑回归的决策边界的基础上,让离直线最近的点尽可能的远(如图离直线较近的 3 个点)
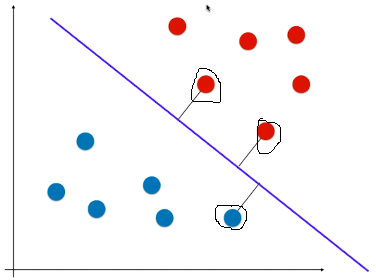
- 思想:SVM 在考虑未来模型的泛化能力时,没有寄望在数据的预处理阶段,或者模型的正则化手段上;而是将泛化能力的考量直接放在了算法的内部,找到一条决策边界,决策边界离不同类型的样本都尽可能的远;
- 疑问:为什么离两种类别的样本都尽可能的远的直线,能对该两类样本更好的划分?
- 原因:直观来看,这种决策边界的泛化能力较好,但这种假设不仅仅根据直观的现象,其背后也有数学理论;(数学中可以证明,面对“不适定问题”,这种方法找到的决策边界,对应的模型的泛化能力较好)正是由于这种原因,SVM 也是统计学中重要的方法,其背后有极强的统计理论知识的支撑;
5)SVM 实现的具体方法
- 决策边界就是根据支撑向量和 margin 所得;
- 支撑向量:特征空间中,距离决策边界最近的不同类型的样本点;(如图所示)
- margin:如图所示,特征空间中,由两类支撑向量决定的两条线的距离;
- 如图:决策边界为中间的那天线;
- margin = 2d
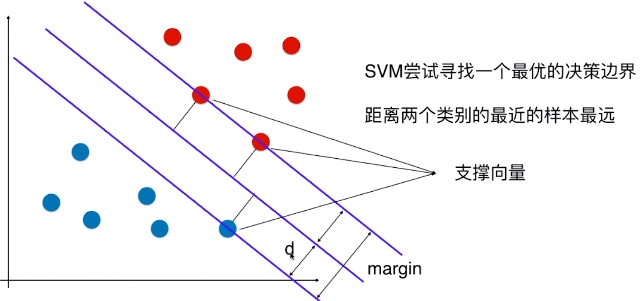
- SVM 算法本质就是要最大化 margin;
6)线性可分、Hard Margin SVM、Soft Margin SVM
- 不管是讨论逻辑回归算法还是 SVM 算法,前提是:样本分布线性可分;
- 线性可分:对于特征空间,存在一条直线或一个平面将样本完全分开
- Hard Margin SVM:
- 解决线性可分问题的 SVM 算法;
- 非常严格的,确实找到了一个决策边界,没有错误的将样本点进行了划分,同时最大化了 margin 的值;
- Soft Margin SVM:
- 解决线性不可分的问题;
- 实践中,大多真实的样本数据是线性不可分的;
- Soft Margin SVM 算法是从 Hard Margin SVM 的基础上改进的;