Finite Markov Decision Process
马尔可夫决策过程(MDP)是对连续决策进行建模,当前的动作不仅对当前产生影响,而且还会对将来的的情况产生影响,如果从奖励的角度,即MDP不仅影响即时的奖励,而且还会影响将来的长期奖励,因此,MDP需要对即时奖励与长期奖励的获得进行权衡。
The Agent-Environment Interface
MDP定义了从交互中学习的框架,决策者(或称为学习者)称为Agent,那与agent交互的所有统称为environment. 二者是连续地进行交互,当agent采取某一动作时,environment对这个动作进行反应,将agent置于新情形,称为状态(state),并且也会对agent的动作进行打分,称为奖励(reward).
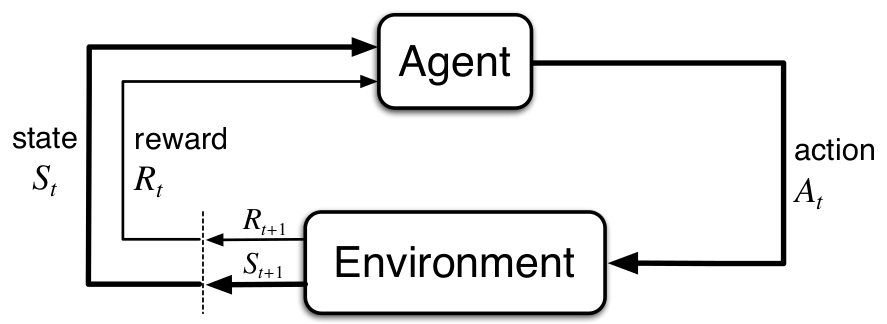
定义环境的状态:(S_t in mathcal{S}) , 动作(A_t in mathcal{A(s)}), 奖励(R_{t+1}in mathcal{R})(注意,这里不同的书惯例是不同的,这里采用的是,当前t时刻agent采取的行动(A_t),环境对其反应的结果是产生(S_{t+1}, R_{t+1}) ,即即时奖励是是在t+1时刻获得)。MDP因此会产生一个包含状态,动作与奖励的决策序列(称为sequence或trajectory):
[S_0,A_0,R_1,S_1,A_1,R_2,...
]
而且,(S_t,R_t)的分布只取决于前一时刻的状态与动作:
[p(s',r|s,a) = Pr{S_t = s',R_t=r|S_{t-1} = s,A_{t-1} = a}
]
其满足:
[sum_{s'inmathcal{S}}sum_{rin mathcal{R}}p(s',r|s,a) = 1,qquad forall sin mathcal{S},ain mathcal{A(s)}
]
有了上面的公式,我们可以推导出很多有用的公式,比如,状态转移概率(state-transition probabilities):
[p(s'|s,a)dot = Pr{S_t = s'|S_{t-1} = s,A_{t-1} = a} = sum_{rin R}p(s',r|s,a)
]
也可以得到状态-动作对的期望奖励:
[r(s,a) dot = E[R_t| S_{t-1} = s, A_{t-1} = a] = sum_{rin mathcal{R}}r sum_{s'in mathcal{S}}p(s',r|s,a)
]
Goals and Rewards
Agent的目标是最大化它能得到的所有奖励的总和,也即最大化累积奖励。使用奖励作为agent的目标,这也是强化学习区别其其它机器学习方法的最显著特征之一。
Returns and Episodes
最大化累积奖励是agent的目标,为能量化这个目标,引入一个概念Returns(用(G_t)表示):
[G_t dot = f(R_{t+1},R_{t+2},...,R_T)
]
其中f是某种映射,T为最后一时间步。
通常最大化Returns的期望:
[max E G_t
]
(G_t)比较常见的版本是加和与折扣(discounted)加和:
[G_t dot = R_{t+1} + R_{t+2} +...+R_T
]
[G_t dot = R_{t+1} + gamma R_{t+2} + gamma^2R_{t+3}+ ... =sum_{k = 0}^{infty} r^k R_{t+k+1}
]
其中(0le gammale 1),称为discount rate.
Policies and Value Functions
策略(policy)是从状态到选择可能动作概率的映射。(pi(a|s)) 表示在状态a下执行动作能的概率。
在给定策略下,状态s的价值函数(value function)是从其状态到最终的期望收益(expected return):
[v_{pi}(s) dot = E_{pi} [G_t |S_t = s] = E_{pi} �ig[sum_{k =0}^{infty}gamma^kR_{t+k+1}�ig|S_t = s �ig], quad forall sin mathcal{S}
]
也可得到动作-价值函数:
[q_{pi}(s,a) dot = E_{pi} [G_t |S_t = s,A_t = a] = E_{pi} �ig[sum_{k =0}^{infty}gamma^kR_{t+k+1}�ig|S_t = s,A_t = a �ig], quad forall sin mathcal{S},a in mathcal{A}
]
价值函数的一个很重要的属性即是其递归性:
[�egin{array}\
v_{pi}(s)&dot =& E_{pi}[G_t | S_t = s]\
&=& E_{pi}[R_{t+1} + gamma G_{t+1}| S_t = s]\
& = & sum_{a}pi(a|s)sum_{s'}sum_{r}p(s',r|s,a)[r +gamma E_{pi}[G_{t+1}| S_{t+1} = s']]\
& =& sum_{a}pi(a|s) sum_{s',r}p(s',r|s,a)[r +gamma v_{pi}(s')],qquad forall s in S
end{array}
]
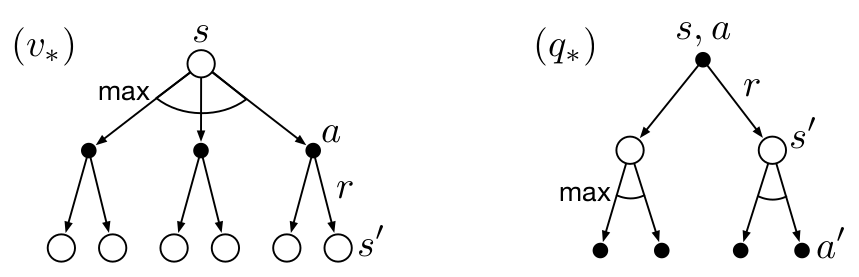
如果我们有一个最优策略((pi_*)),那么这个策略(可能不只一种)可以让价值函数获得最大值,并且根据Bellman equation, 可以得得到如下推导:
[�egin{array}\
v_*(s)&dot = & max_{pi} v_{pi}(s)\
& =& max_{ain mathcal{A(s)}} q_{pi_*}(s,a)\
&=& max_aE_{pi^*}[G_t|S_t = s, A_t = a]\
&=& max_aE[R_{t+1}+gamma v_*(S_{t+1})|S_t = s,A_t = a]\
& =&max_a sum_{s',r}p(s',r|s,a)[r + gamma v_*(s')]
end{array}
]
同理:
[q_*(s,a)dot= max_{pi}q_{pi}(s,a) = E[R_{t+1} + gamma max_{a'}q_*(S_{t+1},a')|S_t = s,A_t = a]= sum_{s',r}p(s',r|s,a)[r + gammamax_{a'}q_*(s',a')]
]
使用 backup diagrams: