1. 题目描述

注: 属于动态规划, 保存已解决的子问题的答案,在需要时再找出已求得的答案, 这样就可以避免大量的重复计算, 节省时间.
可以用一个表来记录所有已解的子问题的答案, 不管该子问题以后是否被用到, 只要它被计算过, 就将其结果填入表中.
2. 代码
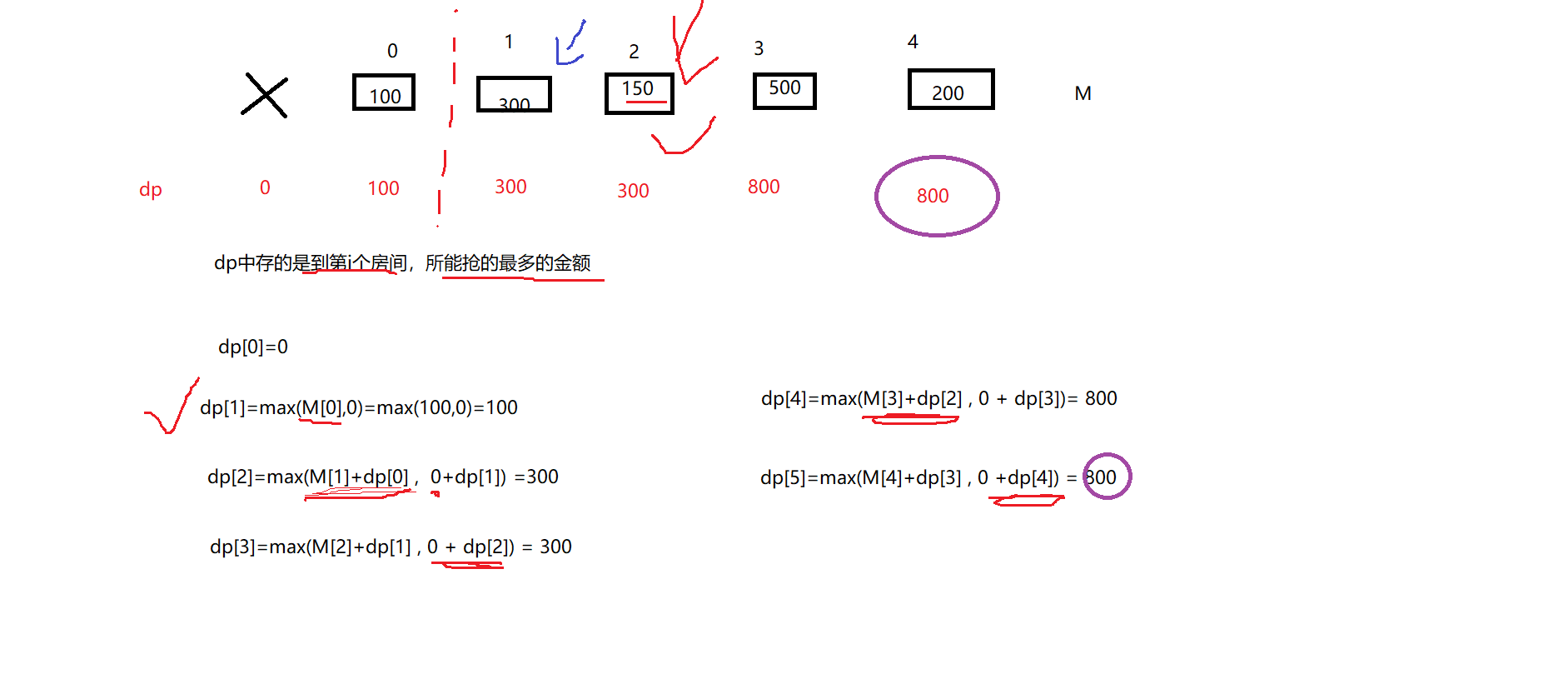
1 class Solution: 2 def rob(self, nums: List[int]) -> int: 3 n = len(nums) 4 if n == 0: 5 return n 6 elif n == 1: 7 return nums[0] 8 elif n == 2: 9 return max(nums[0], nums[1]) 10 11 dp = [0] * (n + 1) 12 dp[0] = 0 13 dp[1] = nums[0] 14 for i in range(2, n+1): 15 dp[i] = max(dp[i-2]+nums[i-1], dp[i-1]) 16 return dp[n]
思路: dp表示当前所能取得的最大钱数.
重点是15行, 取得是 当前元素nums[i-1]和上上个房间的最大值dp[i-2]的和 跟 上个房间的最大值dp[i-1] 的最大值.