编程作业ex1：附加练习

Linear regression with multiple variables—多变量线性回归

ex1data2.txt文件给出了训练样本——第一列是房子大小，第二列是房间数量，第三列是房价

一、特征值缩放

注意到房屋大小为房间数量的1000倍，当特征值达到数量级时，执行特征值缩放可以使梯度下降更快收敛。

记得要存储计算出来的平均值和标准偏差，当我们在预测新的房屋价格时可以利用这些数据对样本进行标准化。

归一化的公式是：。是被归一化的变量集合，是的平均值，是的标准差或偏差。

这里我们使用标准差。MATLAB中使用mean(x),std(x)分别求均值和标准差。

完成featureNormalize.m中的代码：

function [X_norm, mu, sigma] = featureNormalize(X)
X_norm = X;
mu = zeros(1, size(X, 2));  % 平均值初始化为一个1*3的零矩阵
sigma = zeros(1, size(X, 2)); % 标准差初始化为一个1*3的零矩阵
% 遍历X的每一列，对每一列求均值和标准差
% 均值存在mu中，标准差存在sigma中，归一化结果存在X_norm中
for i=1:size(X,2)
    mu(i)=mean(X(:,i)); % 遍历X的每一列，对每一列求均值
    sigma(i)=std(X(:,i)); % 遍历X的每一列，对每一列求标准差
    X_norm(:,i)=(X(:,i)-mu(i))/sigma(i);
end

end

二、代价函数和多变量梯度下降

1. 完成computeCostMulti.m中的代码

复习一下线性回归函数：

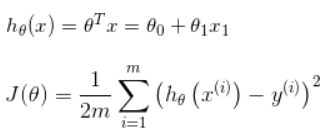
data = load('ex1data1.txt');
X = data(:, 1); y = data(:, 2);
m = length(y); % number of training examples
...
X = [ones(m, 1), data(:,1)]; % Add a column of ones to x
theta = zeros(2, 1); % initialize fitting parameters
...
% compute and display initial cost
J = computeCost(X, y, theta);

从代码看出，X矩阵为数据集的第一列，y矩阵为数据集的第二列，因为theta0前的系数为1，所以要在X前加一列1，通过矩阵运算即可得到J：

等于X*theta-y

等于(X*theta-y)^T*(X*theta-y)，根据矩阵的乘法，结果为一个数，再将这个数除以2m即可得到J。

function J = computeCostMulti(X, y, theta)
m = length(y); % number of training examples
J = 0;
x= X*theta-y;
J=(x'*x)/(2*m);
end

 2.完成gradientDescentMulti.m中的代码

再复习一遍梯度下降的更新公式：

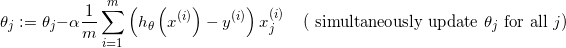
 是学习率（一般取小数），是对求偏导后的结果，

注意的是所有的需要同时更新，同一次迭代中的是不相互影响的。

同样为了运算的直观和方便，也可直接使用矩阵运算，一次运算的到结果。

  是 （）。

要对中每一列都进行一次求内积。然而是一个的列向量，所以先对转置[--]，在和相乘。

结果是

function [theta, J_history] = gradientDescentMulti(X, y, theta, alpha,num_iters)
m = length(y); % number of training examples
J_history = zeros(num_iters, 1);

for iter = 1:num_iters

    x=(alpha*(1/m))*(X'*((X*theta)-y));
    theta=theta-x;

    % Save the cost J in every iteration    
    J_history(iter) = computeCostMulti(X, y, theta);

end

end

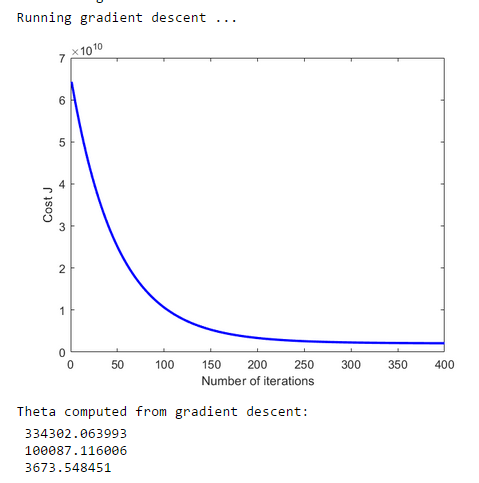
运行结果：

 三、正规方程

区别于迭代的方法，还可以使用正规方程的方法来一步得到解。

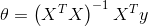
使用此公式不需要任何特征缩放，可以在一次计算中得到一个精确的解决方案；但这个方法通常在X大小适中的时候使用，否在效率会比梯度下降低。

正规方程法和梯度下降法的对比：

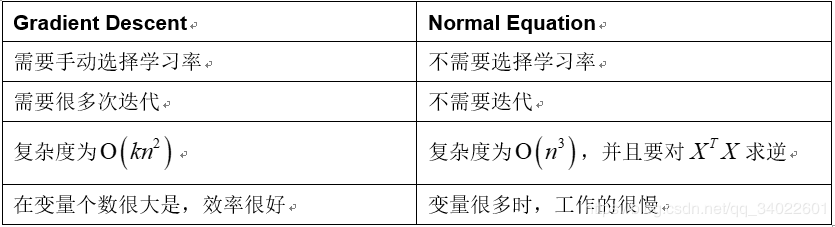
 完成normalE.m中的代码：

function [theta] = normalEqn(X, y)
    theta = zeros(size(X, 2), 1);
    theta = pinv(X'*X)*(X'*y)
end