要求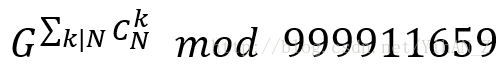
（图是盗来的QAQ）
首先用欧拉定理把幂模一下，直接就是MOD-1了
然后发现MOD-1可以分解为2,3,4679,35617，都是质数，可以直接用Lucas定理
然后用中国剩余定理合并一下即可
千万不可把MOD和MOD-1搞混了，否则调试好麻烦的
1 #include<cstdio> 2 #include<cstdlib> 3 #include<algorithm> 4 #include<cstring> 5 #include<vector> 6 #include<cmath> 7 #define MAXN 35617+10 8 #define ll long long 9 #define pb push_back 10 #define ft first 11 #define sc second 12 #define mp make_pair 13 using namespace std; 14 ll c[5],m[5]={0,2,3,4679,35617}; 15 ll MOD=999911659; 16 ll N,G; 17 ll inv[MAXN],finv[MAXN],fac[MAXN]; 18 ll Pow(ll a,ll b,ll p){ 19 ll ret=1LL; 20 while(b){ 21 if(b&1){ 22 (ret*=a)%=p; 23 } 24 (a*=a)%=p; 25 b>>=1; 26 } 27 return ret; 28 } 29 ll Inv(ll x,ll p){ 30 return Pow(x,p-2,p); 31 } 32 ll C(ll n,ll m,ll p){ 33 if(n<m)return 0LL; 34 return fac[n]*finv[m]*finv[n-m]%p; 35 } 36 ll Lucas(ll n,ll m,ll p){ 37 if(!m)return 1LL; 38 if(n>=p||m>=p){ 39 ll nn=n%p,mm=m%p; 40 if(nn<mm)return 0LL; 41 return Lucas(n/p,m/p,p)*C(nn,mm,p)%p; 42 } 43 else{ 44 return C(n,m,p); 45 } 46 } 47 ll solve(ll p){ 48 fac[0]=fac[1]=1; 49 finv[0]=finv[1]=1; 50 inv[1]=1; 51 for(int i=2;i<p;i++){ 52 fac[i]=fac[i-1]*i%p; 53 inv[i]=p-(inv[p%i]*(p/i)%p); 54 finv[i]=finv[i-1]*inv[i]%p; 55 } 56 ll t=sqrt(1.0*N); 57 ll ret=0LL; 58 for(ll i=1;i<=t;i++){ 59 if(N%i==0){ 60 ret+=Lucas(N,i,p); 61 if(N/i!=i){ 62 ret+=Lucas(N,N/i,p); 63 } 64 } 65 } 66 return ret; 67 } 68 ll CRT(){ 69 ll M=MOD-1; 70 ll ret=0LL; 71 for(int i=1;i<=4;i++){ 72 ll t=Inv(M/m[i],m[i])%M*(M/m[i])%M; 73 ret+=t*c[i]%M; 74 ret%=M; 75 } 76 return ret; 77 } 78 int main() 79 { 80 scanf("%lld%lld",&N,&G); 81 if(G%MOD==0){ 82 printf("0 "); 83 return 0; 84 } 85 for(int i=1;i<=4;i++) c[i]=solve(m[i]); 86 ll x=CRT(); 87 ll ans=Pow(G,x,MOD); 88 printf("%lld ",ans); 89 }