蓝桥杯 试题 历届试题 区间移位 二分

问题描述

　　数轴上有n个闭区间D1,…,Dn。其中区间Di用一对整数[ai, bi]来描述，满足ai < bi。已知这些区间的长度之和至少有10000。所以，通过适当的移动这些区间，你总可以使得他们的“并”覆盖[0, 10000]——也就是说[0, 10000]这个区间内的每一个点都落于至少一个区间内。
　　你希望找一个移动方法，使得位移差最大的那个区间的位移量最小。
　　具体来说，假设你将Di移动到[ai+ci, bi+ci]这个位置。你希望使得maxi |ci|　　最小。

输入格式

　　输入的第一行包含一个整数n，表示区间的数量。
　　接下来有n行，每行2个整数ai,　　bi，以一个空格分开，表示区间[ai, bi]。保证区间的长度之和至少是10000。

输出格式

　　输出一个数，表示答案。如果答案是整数，只输出整数部分。如果答案不是整数，输出时四舍五入保留一位小数。

样例输入

2
10 5010
4980 9980

样例输出

20

样例说明

　　第一个区间往左移动10；第二个区间往右移动20。

样例输入

4
0 4000
3000 5000
5001 8000
7000 10000

样例输出

0.5

样例说明

　　第2个区间往右移0.5；第3个区间往左移0.5即可。

数据规模和约定

　　对于30%的评测用例，1 ≤ n ≤ 10；
　　对于100%的评测用例，1 ≤ n ≤ 10000，0 ≤ ai < bi　　≤ 10000。

---

解题思路：

• 二分：类似最大化最小值( 此题要求的求 最小的max|ci| )或者最小化最大值问题，都可以用二分很好的解决。我们定义：

　　C（ mid ）:任意区间移动的距离都小于等于mid

用二分找到满足条件的d即可。

---

• 每次C( mid )的判断用贪心解决。

这一题可能贪心的策略有很多，比如以左端从小到大排序，按顺序选取满足条件的区间。或者以右端从小到大排序。

以左端从小到大排序可以找到反例说明可能造成有短区间浪费没用到的情况。

而以右端点为什么就不会呢？（这里给一个我的解释，但只是直观解释，没有严格的数学证明）

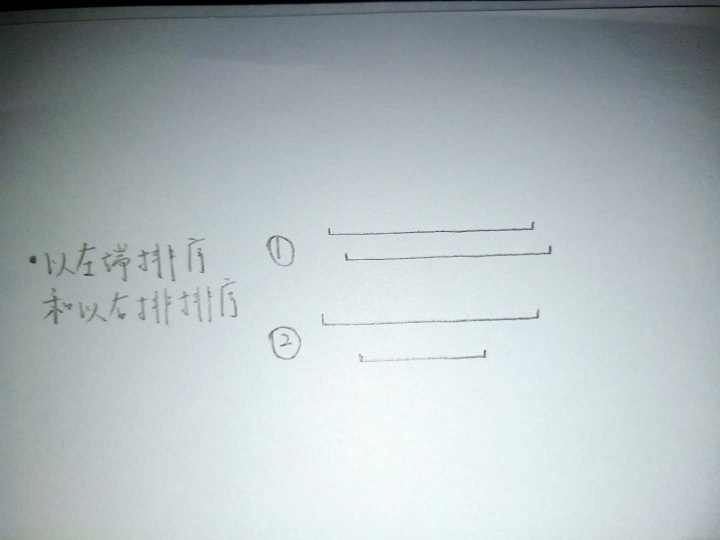
• 对于相邻的两个区间，他们的关系有①②两种，对于关系①,两种排序方式都结果相同；而对于关系②，如果以左端点排序，

可能会造成短区间的浪费，而以右端点排序就会首先考虑段区间，所以综合考虑以右端点排序的方式更优。

• 我们假设cur为当前已经覆盖的连续区间的右端点，每次以右端点从小到大排序选择，则cur相较于其他方案是最小的，

这样右边剩余的空间最大，可以有更多的区间提供选择。

（关于用右端点排序最优的数学证明我还没有想出来，如果哪位大佬知道希望可以指导我一下）

---

对于区间是否选择以及cur的更新：

　　　　假设当前区间可以移动的最大距离为mid, 那么某个区间可以移动的范围为 [ l - mid, r + mid ],满足这个条件的区间可以使用，与cur有如下四种关系：

　　综合之后 ①②为一种情况，③④为一种情况。

---

• 最后可能有小数的情况，因为刚开始区间位置都是整数，设如果一个区间要移动x( x为小数 )，那么就有一个区间要移动 y （y为小数），且x+y=z, z为整数，

题目要求最小，那么 x==y==z/2，所以处理时只需要将每个区间都乘以2，最后判断结果是否能被2整除。

---

• 实现代码：

#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;

//输入
int n; 

struct node//区间 
{
    int l;
    int r;
    node(int l1,int r1){ l = l1 ; r = r1;}//构造函数 
};

vector<node> v;

bool cmp(node n1, node n2)
{
    if( n1.r==n2.r )    return n1.l<n2.l;//如果右端点相等，选择更接近cur的 
    return n1.r<n2.r;//以右端点从小到大排序 
}

bool C(int mid)//判断mid是否满足条件 
{
    int cur = 0;
    vector<node> v_(v);
    
    while( true )
    {
        bool flat = false;//有没有满足条件的区间 
        for(int i=0; i<v_.size(); i++)
        {
            int l = v_[i].l, r = v_[i].r;
            if( l-mid<=cur&&cur<=r+mid )//满足条件 
            {
                if( cur-l>=mid )//情况 1,2 
                {
                    //cur += mid + r - cur;
                    cur = mid+r;
                }
                else//情况 3,4 
                {
                    cur += (r-l);// cur += len
                }
                v_.erase(v_.begin()+i);//去掉此区间 
                flat = true;
                break;//每次找到一个区间cur的状态都改变,原来不能移动的区间现在可能可以移动 
            }
        }
        if( !flat || cur>=20000 )    break;//如果没有满足条件的区间||已经覆盖了所有区间 
    }
    return cur>=20000;
}

void solve()
{
    sort(v.begin(),v.end(),cmp);
    
    int l = 0, r = 20000;
    while( r-l>1 )//二分法求解 
    {
        int mid = (l+r)/2;
        if( C(mid) )    r = mid;//满足条件,缩小移动距离 
        else    l = mid;
    }
    
    if( r%2==0 )    printf("%d
",r/2);
    else    printf("%.1f
",(float)r/2.0);
}

int main()
{
    scanf("%d",&n);
    while( n-- )
    {
        int l,r;
        scanf("%d%d",&l,&r);
        v.push_back(node(2*l,2*r));//每个区间乘以2 
    }
    
    solve();
    
    return 0;
}